Принципы многомерного сравнения объектов

Рассмотрим два объекта  и  и 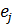оценим принципы, которые позволят обоснованно утверждать, что один из них предпочтительнее другого.

Очевидно, что если существует такой объект , для которого оценка  для любого 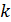 больше либо равна соответствующей оценке  объекта 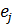, то тогда, безусловно, можно утверждать, что  предпочтительнее .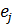

Если же оценки объектов по разным критериям противоречивы, то для осуществления процедуры сравнения таких объектов необходимо все множество критериев  разделить на два подмножества:  – множество критериев, согласно которым , по крайней мере, не хуже, чем 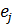;  – множество критериев, для которых это утверждение не выполняется.

Показатели соответствия. Очевидно, что чем большее число критериев входит в , тем более обоснованно принять предположение, что  предпочтительнее 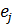. Кроме того, необходимо учесть различную важность, значимость критериев, определяемую коэффициентами 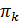. Поэтому для оценки степени соответствия различных критериев нашей гипотезе вводится показатель соответствия , определяемый по формуле (36):

                                                          (36)

Этот показатель обладает следующими свойствами:

1.

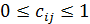
2. 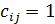, если .

Показатель соответствия рассчитывается для каждой пары объектов  и 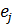. Результаты таких расчетов могут быть представлены в матрице  , каждый элемент которой  есть показатель соответствия предположению, что объект  предпочтительнее объекта 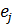. Легко видеть, что такая матрица, как правило, не симметрична. Элементы  не имеют смысла в данной задаче, а потому в таблицу не вносятся.

Показатели несоответствия. Для осуществления процедуры сравнения необходимо учесть и критерии, противоречащие введенному предложению, что объект , по крайней мере, не хуже объекта 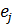. С этой целью рассчитывается так называемый показатель несоответствия . Для его получения необходимо:

а) вычислить разности между оценками объектов  и  для  и упорядочить полученные отклонения в невозрастающую последовательность;

б) определить показатель несоответствия  как s-ый член построенной последовательности, нормированный по высоте самой большой шкалы.

Нормирование осуществляется с целью учета относительной значимости принимаемых во внимание критериев, так как высота шкалы (разность между высшей и низшей оценками) является неубывающей функцией коэффициента значимости критерия .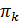

Очевидно, что такое определение показателя несоответствия, например, для , эквивалентно исключению из рассмотрения критерия с самым большим несоответствием, для  – исключению двух критериев c наибольшими несоответствиями и т.д., как бы ни было велико это несоответствие.

Значения показателей несоответствия для всех пар () могут быть представлены в таблице .

Сформулируем принцип сравнения объектов по нескольким критериям.

Фиксируем значение параметра , затем задаем два числа:  (порог соответствия) и  (порог несоответствия) и говорим, что согласно  критериям и порогам  и  объект  предпочтительнее объекта 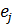, если и только если пара () приводит к показателю соответствия  и показателю несоответствия .

Предпочтение, определенное таким образом, удобно представлять в виде графа:

,

где  – множество вершин графа, соответствующее множеству рассматриваемых объектов;  – множество дуг графа, дуга  и . Очевидно, что чем меньше требования к значениям  и , тем более соответствующий граф богат дугами. Однако сравнение и выбор, проводимые на основе очень слабых требований к  и , могут не отражать реальную ситуацию выбора. Поэтому необходимо последовательно и постепенно ослаблять требования к параметрам  и анализировать возникающие связи.

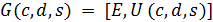Таким образом, для каждой тройки () мы можем построить , при этом множество вершин графа  может быть разделено на два непересекающиеся подмножества  и . Подмножество  таково, что всякий элемент, не включенный в , будет превзойден, по крайней мере, одним элементом, принадлежащим . Это свойство называется свойством внешней стабильности подмножества . Другое свойство этого множества – свойство внутренней стабильности означает, что никакой элемент  не превосходит другого элемента , т.е. элементы  несравнимы между собой при заданных . Подмножество вершин графа, которое обладает этими двумя свойствами, носит название ядра графа. Можно доказать, что граф, не имеющий циклов, имеет ядро, причем единственное.

Естественно предположить, что наличие цикла в графе указывает на эквивалентность объектов, составляющих этот цикл.

Таким образом, всегда можно выделить ядро  графа . Подмножество  может иметь различное число элементов. Если для заданных параметров  ядро включает очень много элементов – это означает, что антагонизм критериев таков, что не позволяет осуществить достаточное сравнение объектов при этих параметрах. Уменьшение требовательности к порогам  и  сократит число элементов  и, наоборот, усиление требований к ним влечет за собой обогащение .

Таким образом, в результате исследования поведения графов и их ядер, в зависимости от изменения параметров , можно предложить ответственному за решение небольшое подмножество объектов-кандидатов, рассматривая которые он может осуществить выбор, так как самый хороший объект, наверняка, находится в нем. Выбор среди элементов  может быть осуществлен на основании дополнительных критериев, экспериментов, расчетов, проведение которых для всех объектов  может быть по каким-то причинам нерациональным – слишком дорого, слишком долго и т.д. Таким обрезом, метод позволяет формализовать выбор одного объекта среди многих.

Кроме того, исследование поведения графов и их ядер с изменением  и  позволяет установить некоторую классификацию, упорядочивая объекты множества  в последовательность, благодаря которой каждый объект может быть сравним с другим по своей позиции в этой последовательности. Исследование таблиц  и  поможет определить, какие из сравниваемых объектов являются «близкими», можно выделить из них почти эквивалентные, образующие циклы и т.п.