 |
Введение. Содержание.. 1. Векторное поле, векторные линии.
|
|
|
|
Введение.
Предлагаемое учебное пособие предназначено студентам заочного отделения, для выполнения индивидуальных домашних заданий по курсу «Математический анализ» по следующим разделам векторного анализа: криволинейные и поверхностные интегралы второго рода.
В представленном пособии кратко изложены теоретические вопросы и приведены подробные решения типовых задач, предлагаемых в качестве индивидуальных домашних заданий.
Основное внимание в пособие уделено задачам на вычисление работы векторного поля; определению потенциала векторного поля; вычислению потоков векторного поля.
В «Приложении» приведены варианты индивидуальных домашних заданий по вышеуказанным разделам «Математического анализа»; уравнения и вид поверхностей второго порядка, наиболее часто встречающихся в задачах; вопросы к экзамену по векторному анализу и рекомендуемая литература.
Данное пособие предназначено, в основном, студентам заочного отделения для самостоятельного изучения вышеуказанных разделов курса «Математический анализ», однако, пособие может быть полезным и студентам дневного отделения при выполнении индивидуальных домашних заданий.
Содержание.
1. Векторное поле, векторные линии…………………………………..
2. Криволинейный интеграл второго рода……………………………..
2. 1. Связь между криволинейными интегралами первого и
второго рода…………………………………………………………
2. 2. Свойства криволинейных интегралов второго рода………………..
2. 3. Физический и механический смысл криволинейного
интеграла второго рода………………………………………………
2. 4. Условия независимости криволинейного интеграла
|
|
|
второго рода от формы пути интегрирования………………………
2. 5. Оператор Гамильтона…………………………………………………
2. 6. Формула Грина………………………………………………………..
3. Поверхностный интеграл второго рода……………………………..
3. 1. Свойства поверхностных интегралов второго рода………………...
3. 2. Вычисление поверхностных интегралов второго рода……………..
3. 2. 1. Метод проектирования на три координатные плоскости…………..
3. 2. 2. Связь между поверхностными интегралами первого
и второго рода…………………………………………………………
3. 2. 3. Метод проектирования на одну координатную плоскость……….
3. 2. 4. Метод Остроградского-Гаусса……………………………………...
4. Формула Стокса……………………………………………………….
Приложения………………………………………………………………..
1. Векторное поле, векторные линии.
Если каждой точке М(х, у, z) трехмерного пространства соответствует определенное значение скалярной величины U(M), то поле этой величины называется скалярным полем. Примером скалярных полей могут служить поле температур, электростатическое поле и т. д.
Геометрической характеристикой скалярного поля являются поверхности уровня, или в двумерном пространстве – линии уровня. Поверхности уровня – геометрическое мести точек, где функция U(х, у, z) = const.
Если в каждой точке М пространства или части пространства определена векторная величина ā = ā (М), то говорят, что задано векторное поле.
Если в пространстве введена декартовая система координат, то задание векторного поля ā = ā (М) равносильно заданию трех скалярных функций P(M), Q(M), R(M) так, что
 (M) = P(x, y, z)
(M) = P(x, y, z)  + Q(x, y, z)
+ Q(x, y, z)  + R(x, y, z)
+ R(x, y, z) 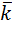 ,
,
где P(x, y, z), Q(x, y, z), R(x, y, z) –непрерывные функции трех переменных, имеющие частные производные первого порядка.
Геометрической характеристикой векторного поля являются векторные линии. Векторной линией векторного поля  называется линия в пространстве, в каждой точке М(x, y, z) которой касательная к ней совпадает с направлением вектора
называется линия в пространстве, в каждой точке М(x, y, z) которой касательная к ней совпадает с направлением вектора 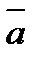 (М).
(М).
|
|
|
Векторное поле называется плоским, если все векторы α (М) расположены в параллельных плоскостях и поле одно и то же в каждой из этих плоскостей, а компоненты вектора α (М) будут зависеть только от двух координат точки М(х, у).
2. Криволинейный интеграл второго рода.
Пусть АВ – кусочно-гладкая ориентированная дуга пространственной кривой (рис 2. 1), на которой определена и непрерывна некоторая векторная функция 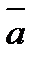 (М) с координатами:
(М) с координатами: 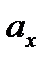 = P(x, y, z),
= P(x, y, z),  = Q(x, y, z),
= Q(x, y, z),  = R(x, y, z).
= R(x, y, z).
z
Mi-1
Ni(xi, yi, zi)
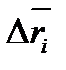
M1 Mi
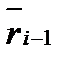
A=M0 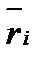 B=Mn
B=Mn
0
y
x
Рис. 2. 1
Разобьем дугу АВ произвольным образом в направлении от точки А к точке В с помощью точек 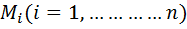 на n частичных дуг:
на n частичных дуг:
∆ l1, ∆ l2, …, ∆ ln.
Пусть 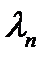 наибольшая из частичных дуг (если
наибольшая из частичных дуг (если  , то
, то 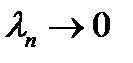 ). Выберем произвольным образом точки
). Выберем произвольным образом точки 
Пусть вектор  .
.
Вычислим значения координат векторной функции в точках Ni.
Составим интегральную сумму:

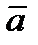 (N
(N  ) ∆
) ∆ 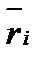 =
=  (P(N
(P(N  ) ∆ x
) ∆ x  + Q(N
+ Q(N  ) ∆ y
) ∆ y  + R(N
+ R(N 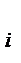 ) ∆ Z
) ∆ Z 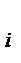 )
)
Предел интегральной суммы при n 
 , если он существует и конечен, а также не зависит ни от способа разбиения дуги AB на частичные дуги, ни от выбора точек Ni, называется криволинейным интегралом второго рода по дуге AB.
, если он существует и конечен, а также не зависит ни от способа разбиения дуги AB на частичные дуги, ни от выбора точек Ni, называется криволинейным интегралом второго рода по дуге AB.
 (2. 1)
(2. 1)
Условия существования криволинейного интеграла второго рода: дуга AB должна быть кусочно-гладкой, а функции P(x, y, z), Q(x, y, z), R(x, y, z) – непрерывны на дуге АВ.
|
|
|
|
|
|


