 |
2.4. Условия независимости криволинейного интеграла второго рода от формы пути интегрирования.
|
|
|
|
2. 4. Условия независимости криволинейного интеграла второго рода от формы пути интегрирования.
Интеграл
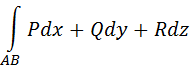
в некоторой области пространства XYZне зависит от формы пути интегрирования, если его значения по всевозможным кусочно-гладким кривым, лежащим в данной области и имеющим общее начало и общий конец, одинаковы.
Теорема. Для того, чтобы интеграл
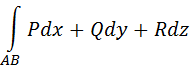
где P(x, y, z), Q(x, y, z), и R(x, y, z) – непрерывные функции, имеющие непрерывные частные производные первого порядка, в области пространства XYZ, не зависел от формы пути интегрирования, необходимо и достаточно, чтобы выражение  было полным дифференциалом некоторой скалярной функции U(x, y, z).
было полным дифференциалом некоторой скалярной функции U(x, y, z).
При этом необходимо и достаточно выполнение следующих условий:
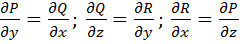 . (2. 5)
. (2. 5)
Векторное (силовое) поле будет являться потенциальным в данной области, если в этой области выполняются условия (2. 5). Криволинейный интеграл второго рода (работа в потенциальном поле) не зависит от формы пути интегрирования, или, что тоже, циркуляция (работа) поля по любому замкнутому контуру равна нулю. Таким образом, равенства (2. 5) представляют собой условияпотенциальности векторного поля.
Вычисление потенциала векторного поля.
Так как в потенциальном поле (выполнение условий (2. 5)) криволинейный интеграл второго рода не зависит от формы пути интегрирования, то в качестве кривой L, вдоль которой будем вычислять криволинейный интеграл, возьмем ломаную линию, звенья которой параллельны осям координат. Зафиксируем начальную точку A( 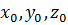 ) и соединим ее ломаной линией с текущей точкой B(x, y, z). Рассмотрим данный способ нахождения потенциала векторного поля на примере.
) и соединим ее ломаной линией с текущей точкой B(x, y, z). Рассмотрим данный способ нахождения потенциала векторного поля на примере.
|
|
|
Пример: вычислить потенциальную функцию векторного поля
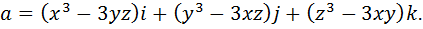
Начнем решение задачи с проверки условий (2. 5) потенциальности заданного векторного поля.

Тогда потенциальная функция
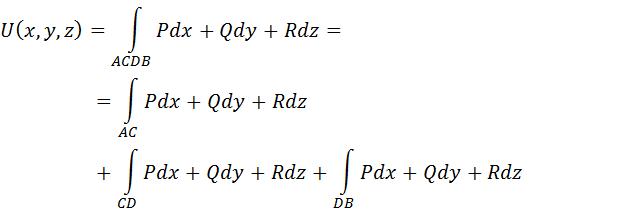
где

Рассмотрим интегралы вдоль каждого отрезка ломаной линии.
В данном примере в качестве начальной точки A( 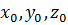 ) было взято начало координат A(0, 0, 0). Если же функции P(x, y, z), Q(x, y, z), и R(x, y, z) в начале координат не существуют, то обычно, в качестве начальной, берут точку с координатами A(1, 1, 1), либо любую другую.
) было взято начало координат A(0, 0, 0). Если же функции P(x, y, z), Q(x, y, z), и R(x, y, z) в начале координат не существуют, то обычно, в качестве начальной, берут точку с координатами A(1, 1, 1), либо любую другую.
Второй способ вычисления функции  :
:
 (2. 6)
(2. 6)
Для данной задачи найдем потенциальную функцию, используя формулу (2. 6):
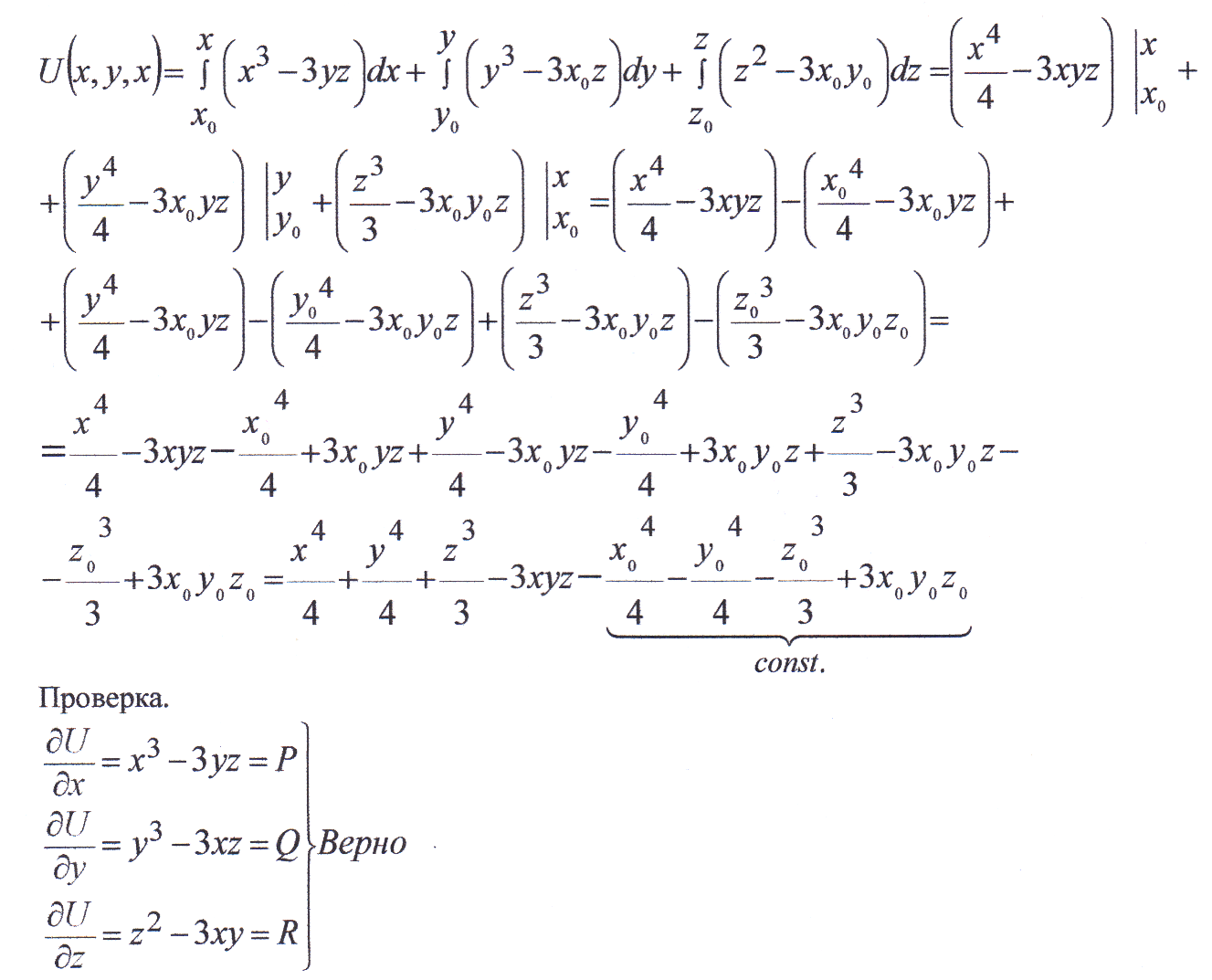
После окончательного решения задачи всегда следует делать проверку.
Пример: вычислить потенциальную функцию векторного поля двумя способами.
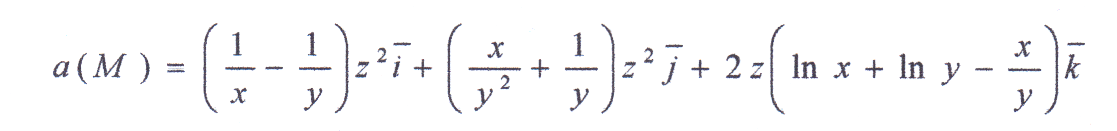
Проверим потенциальность векторного поля:

Условия (2. 5) выполнены, следовательно, заданное поле потенциально.



U(x, y, z) = Z² ∙ (ln x + ln y – (x/y)) + 1
2 способ вычисления потенциальной функции в соответствии с формулой (2. 6):


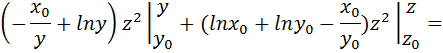
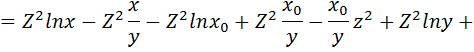

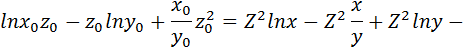
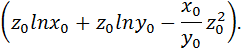
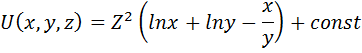
Проверим полученную потенциальную функцию:
Ответ: 

Пример: вычислить потенциальную функцию плоского векторного поля двумя способами.

Проверка условий потенциальности векторного поля.
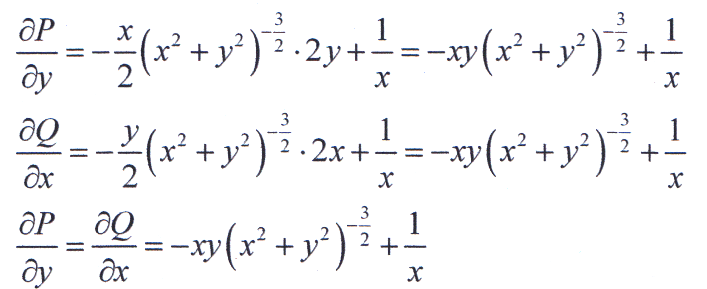
Следовательно, поле потенциально.
1-ый способ нахождения потенциальной функции.
Т. к. криволинейный интеграл 2-ого рода не зависит от формы пути интегрирования, примем за путь интегрирования ломаную линию АСВ, где линия АС параллельна оси ОХ, линия СВ параллельна оси ОУ. Т. к. функции P(x, y) и Q(x, y) не существуют в начале координат, то за начальную точку выберем точку с координатами (1, 1).
2-ой способ (формула (2. 6))

2. 5. Оператор Гамильтона
Многие операции векторного анализа могут быть записаны в сокращенной и удобной для расчетов форме путем введения символического дифференцирующего вектора набла  , называемого оператором Гамильтона.
, называемого оператором Гамильтона.
|
|
|
Ротором вектора 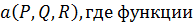
 и их первые частные производные непрерывны в некоторой области 3-х мерного пространства, называется вектор, получаемый в результате векторного произведения символического вектора
и их первые частные производные непрерывны в некоторой области 3-х мерного пространства, называется вектор, получаемый в результате векторного произведения символического вектора 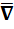 и вектора
и вектора  .
.

(2. 7)
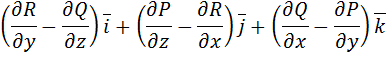
Если  , то векторное поле
, то векторное поле 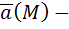 потенциально, т. к. если координаты вектора
потенциально, т. к. если координаты вектора 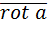 равны нулю, то мы получаем условия потенциальности векторного поля (2. 5). Потому в задачах на нахождение потенциальной функции при проверке условий потенциальности векторного поля можно использовать либо условия потенциальности (2. 5), либо вычислять
равны нулю, то мы получаем условия потенциальности векторного поля (2. 5). Потому в задачах на нахождение потенциальной функции при проверке условий потенциальности векторного поля можно использовать либо условия потенциальности (2. 5), либо вычислять 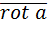 .
.
Пример: вычислить потенциальную функцию плоского векторного поля 
Решение начнем с нахождения 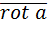 .
.



Следовательно, поле 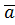 является потенциальным. Найдем потенциальную функцию, используя формулу (2. 6):
является потенциальным. Найдем потенциальную функцию, используя формулу (2. 6):
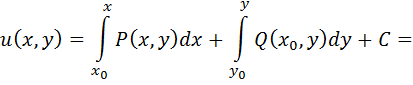
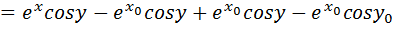
Проверка:
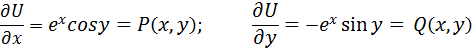
Кроме ротора векторного поля с помощью символического вектора набла можно найти градиент скалярной функции  , путем простого умножения вектора набла на скалярную функцию
, путем простого умножения вектора набла на скалярную функцию 
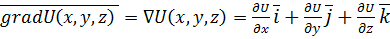 (2. 8)
(2. 8)
Скалярное произведение вектора  и вектора векторного поля
и вектора векторного поля  называется дивергенцией векторного поля. Дивергенция – величина скалярная и вычисляется следующим образом:
называется дивергенцией векторного поля. Дивергенция – величина скалярная и вычисляется следующим образом:
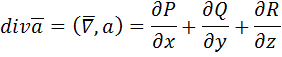 (2. 9)
(2. 9)
|
|
|


