 |
3.2. Вычисление поверхностных интегралов второго рода.
|
|
|
|
3. 2. Вычисление поверхностных интегралов второго рода.
К вычислению поверхностных интегралов второго рода приводит задача о потоке векторного поля. Существует несколько основных методов вычисления поверхностных интегралов второго рода.
3. 2. 1. Метод проектирования на три координатные плоскости.
В соответствии с формулами (3. 1), (3. 2), (3. 3) вычисление поверхностного интеграла второго рода может быть сведено к вычислению трех двойных интегралов по проекциям области S на соответствующие координатные плоскости. Знаки перед интегралами выбираются в зависимости от ориентации поверхности S: если нормаль к поверхности с соответствующей осью координат образует острый угол, то берется знак «плюс», а если тупой угол – знак «минус».
Пример: вычислить поверхностный интеграл второго рода
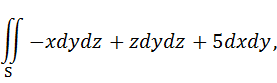
если S – верхняя сторона плоскости 2x – 3y + z = 6
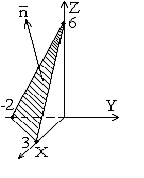 рис. 3. 2
рис. 3. 2
Проектируем поверхность S на плоскость YOZ:
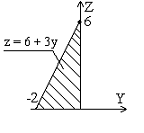 Тогда
Тогда
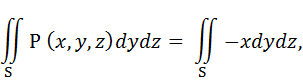
рис. 3. 3 где из уравнения плоскости  , тогда получим двойной интеграл по проекции S на YOZ.
, тогда получим двойной интеграл по проекции S на YOZ.
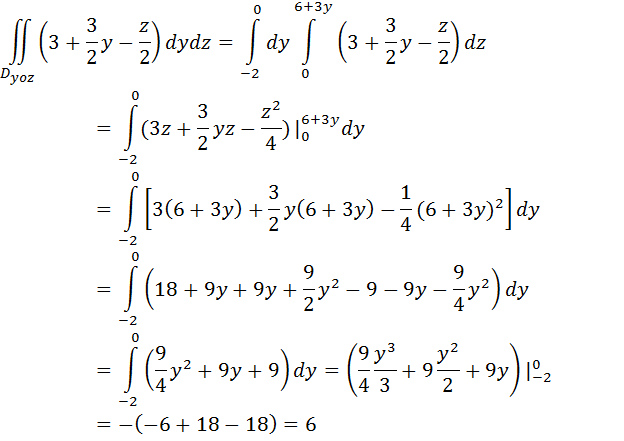
Так как нормаль с осью OX составляет острый угол, то в общей сумме этот интеграл возьмем со знаком «плюс», т. е. I1 = 6.
Проектируем поверхность S на плоскость XOZ. Проекция является также треугольником, ограниченным наклонной линией и отрезками координатных осей.
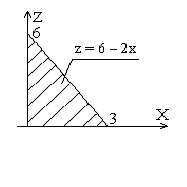 рис. 3. 4
рис. 3. 4
Тогда, соответствующий поверхностный интеграл примет вид:
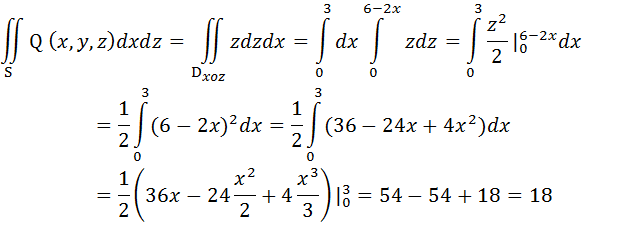
Но так как нормаль к поверхности S составляет с осью OY тупой угол, то в общей сумме этот интеграл возьмем со знаком «минус», т. е. I2 = -18.
Проектируем поверхность S на плоскость XOY:
 рис. 3. 5
рис. 3. 5
Тогда

Так как нормаль к поверхности S составляет с осью OZ острый угол, то в общей сумме этот интеграл возьмем со знаком «плюс», т. е. I3 = 15.
|
|
|
Тогда, окончательный результат:
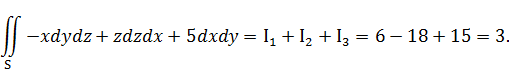
3. 1. 2. Связь между поверхностными интегралами
первого и второго рода.
Пусть S – поверхность, заданная уравнением z=f(x, y), где функции f(x, y), f 'x(x, y), f 'y(x, y) - непрерывны в замкнутой области Dxy – проекции поверхности S на плоскость XOY, а функция R(x, y, z) – непрерывна на поверхности S. Выберем верхнюю сторону поверхности S.
Разобьем поверхность S сетью кусочно-гладких кривых на n частей ∆ S1, ∆ S2, … ∆ Sn. Проекциями этих линий область Dxy разобьется на части, обозначенные соответственно ∆ σ 1, ∆ σ 2, … ∆ σ n.
При этом
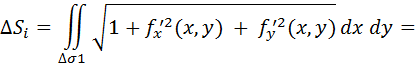

где Pi 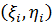 – некоторая точка области
– некоторая точка области  .
.
Обозначим через Мi  точку поверхности
точку поверхности  , соответствующую точке Pi , а через
, соответствующую точке Pi , а через  – острый угол, образованный нормалью к поверхности S в точке Мi с осью OZ. Тогда
– острый угол, образованный нормалью к поверхности S в точке Мi с осью OZ. Тогда

Составляя интегральную сумму для поверхностного интеграла второго рода по верхней стороне поверхности S, получим:

Сумма 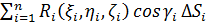 является интегральной суммой для интеграла первого рода по поверхности S от функции R(x, y, z)
является интегральной суммой для интеграла первого рода по поверхности S от функции R(x, y, z) 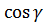 [
[  – угол, составленный с осью OZ нормалью в текущей точке M(x, y, z) к поверхности S в выбранную сторону поверхности]. При стремлении шага разбиения к нулю в пределе будем иметь:
– угол, составленный с осью OZ нормалью в текущей точке M(x, y, z) к поверхности S в выбранную сторону поверхности]. При стремлении шага разбиения к нулю в пределе будем иметь:

Аналогичные формулы при соответствующих условиях имеют место для двух других составляющих поверхностного интеграла. Суммируя, получаем формулу вычисления поверхностного интеграла второго рода через поверхностный интеграл первого рода:
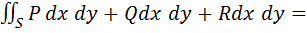 (3. 4)
(3. 4)
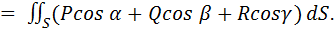
Здесь  ,
,  ,
, 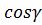 – направляющие косинусы единичной нормали к поверхности S в выбранную (для интеграла слева) сторону поверхности.
– направляющие косинусы единичной нормали к поверхности S в выбранную (для интеграла слева) сторону поверхности.
|
|
|
Пример: найти поток векторного поля  =2x
=2x  +y
+y  +z
+z 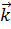 через внешнюю часть плоскости S, расположенную в первом октане x+y+z=1.
через внешнюю часть плоскости S, расположенную в первом октане x+y+z=1.

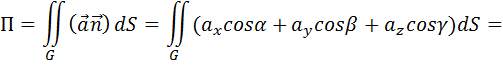
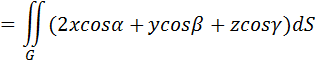

 ,
, 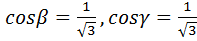 ; z=1-x-y
; z=1-x-y




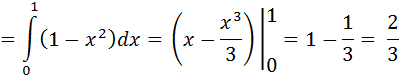
|
|
|


