 |
2.1. Связь между криволинейными интегралами
|
|
|
|
2. 1. Связь между криволинейными интегралами
первого и второго рода.
Пусть криволинейный интеграл второго рода по пространственной кривой АВ имеет вид:
 P(x, y, z)dx+Q(x, y, z)dy+R(x, y, z)dz
P(x, y, z)dx+Q(x, y, z)dy+R(x, y, z)dz
Рассмотрим вектор-функцию
F(x, y, z) = P(x, y, z)i + Q(x, y, z)j + R(x, y, z)k
как трёхмерный вектор с компонентами P(x, y, z), Q(x, y, z) и R(x, y, z), а также вектор dr=dx∙ i+dy∙ j+dz∙ k. Тогда комбинация, стоящая под знаком интеграла, есть не что иное, как скалярное произведение векторов 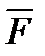 (x, y, z) и
(x, y, z) и 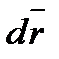 , т. е.
, т. е.
P(x, y, z)dx+Q(x, y, z)dy+R(x, y, z)dz = (  (x, y, z)
(x, y, z)  ), и поэтому
), и поэтому
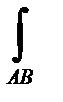 P(x, y, z)dx + Q(x, y, z)dy + R(x, y, z)dz =
P(x, y, z)dx + Q(x, y, z)dy + R(x, y, z)dz = 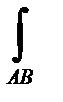 (
(  (x, y, z),
(x, y, z), 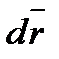 ).
).
Обозначим через α, β и γ углы, которые вектор 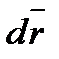 образует с осями OX, OY и OZ. Заметим, что длина вектора
образует с осями OX, OY и OZ. Заметим, что длина вектора  :
:
 =
=  =ds
=ds
есть не что иное, как дифференциал длины дуги кривой. Поэтому
 dx=ds∙ cosα, dy=ds∙ cosβ, dz=ds∙ cosγ
dx=ds∙ cosα, dy=ds∙ cosβ, dz=ds∙ cosγ
и мы можем записать
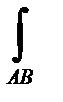 Pdx+Qdy+Rdz=
Pdx+Qdy+Rdz= 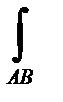 (Pcosα +Qcosβ +Rcosγ )ds (2. 2)
(Pcosα +Qcosβ +Rcosγ )ds (2. 2)
Заметим, что слева стоит криволинейный интеграл второго рода, а справа – криволинейный интеграл первого рода. Эта формула даёт связь между криволинейными интегралами первого и второго рода.
2. 2. Свойства криволинейных интегралов второго рода.
1. Постоянный множитель выносится за знак криволинейного интеграла
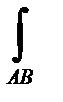 k P(x, y, z)dx=k
k P(x, y, z)dx=k 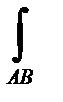 P(x, y, z)dx
P(x, y, z)dx
Свойства криволинейных интегралов второго рода будем рассматривать на одной из составляющих криволинейного интеграла.
2. Криволинейный интеграл от суммы функции равен сумме интегралов
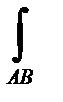 (P1(x, y, z)+P2(x, y, z))dx=
(P1(x, y, z)+P2(x, y, z))dx= 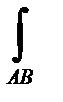 P1(x, y, z)dx+
P1(x, y, z)dx+ 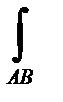 P2(x, y, z)dx
P2(x, y, z)dx
3. Если кривая AB разбивается точкой С на две части, то
 Pdx=
Pdx=  Pdx +
Pdx + 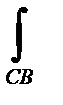 Pdx
Pdx
4. Криволинейный интеграл второго рода по замкнутой кривой (циркуляция) не зависит от выбора начальной точки, а зависит только от направления обхода данной кривой.
|
|
|
5. Если AB – кривая, лежащая в плоскости, перпендикулярной оси OX, то
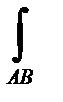 P(x, y, z)dx=0,
P(x, y, z)dx=0,
Если дуга AB принадлежит плоскости, перпендикулярной оси OY, то
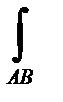 Q(x, y, z)dy=0,
Q(x, y, z)dy=0,
если дуга AB лежит в плоскости, перпендикулярной оси OZ, то
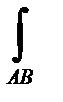 R(x, y, z)dz=0
R(x, y, z)dz=0
2. 3. Физический и механический смысл криволинейного интеграла второго рода.
Физически функция F(x, y, z) ассоциируется с силовым полем, если в каждой точке пространства на материальною точку действует сила F(x, y, z). Примером такого поля может служить гравитационное поле, электрическое поле, магнитное поле и т. д. Физически скалярное произведение (F(x, y, z), dr)=dA имеет смысл работы, которое силовое поле F(x, y, z) совершает, перемещая материальную точку по вектору dr. Поэтому, с точки зрения физики, криволинейный интеграл второго рода
A= 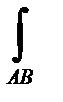 (
(  (x, y, z),
(x, y, z),  ) (2. 3)
) (2. 3)
есть работа, которую совершает силовое поле  (x, y, z), перемещая материальную точку по кривой AB.
(x, y, z), перемещая материальную точку по кривой AB.
Вычисление криволинейных интегралов второго рода.
Пусть кривая AB задана параметрическими уравнениями x=X(t), y=Y(t), z=Z(t), где 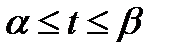 тогда
тогда 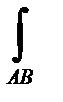 P(x, y, z)dx+Q(x, y, z)dy+R(x, y, z)dz=
P(x, y, z)dx+Q(x, y, z)dy+R(x, y, z)dz=  [P(t)∙
[P(t)∙  +Q(t)∙
+Q(t)∙  +R(t)
+R(t)  ]dt (2. 4)
]dt (2. 4)
Пример: вычислить работу векторного поля силы  при движении материальной точки вдоль дуги L винтовой линии:
при движении материальной точки вдоль дуги L винтовой линии:
x=Rcost; y=Rsint; z= 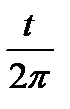 от
от 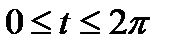
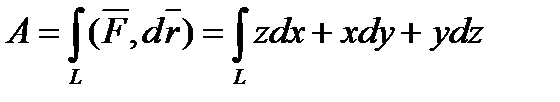
dx=-Rsint dt; dy=Rcost dt; dz= 
 =
=
= 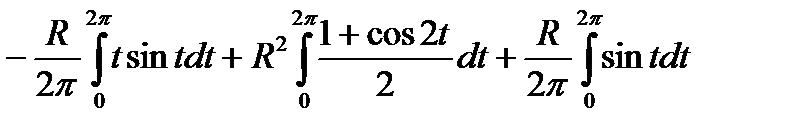
Вычислим первый интеграл, используя формулу «интегрирования по частям»:

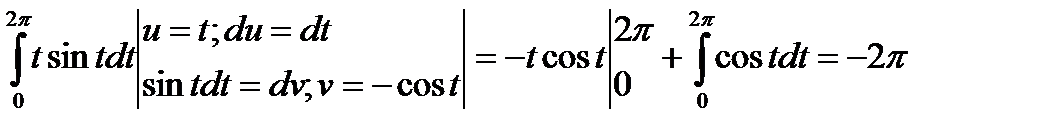
Вычислим второй интеграл:

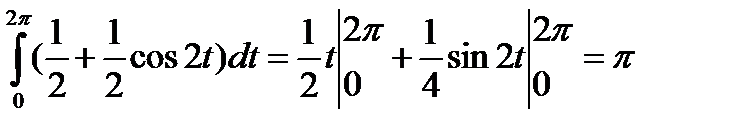

Третий интеграл в заданных пределах будет равен нулю.
Тогда 
Пример: вычислить работу силового поля 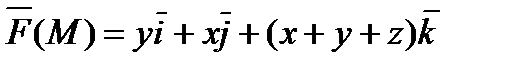 вдоль отрезка AB, соединяющего точки A(2; 3; 4) и B(3; 4; 5).
вдоль отрезка AB, соединяющего точки A(2; 3; 4) и B(3; 4; 5).
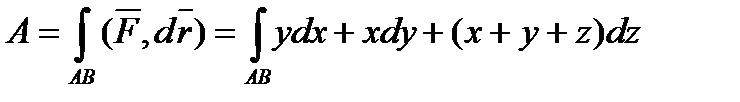
Находим каноническое уравнение прямой AB:

Переходим к параметрическому уравнению прямой линии АВ:
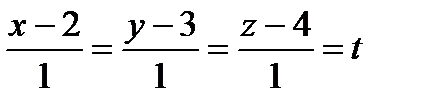 ,
,
следовательно, х=t+2; y=t+3; z=t+4, где параметр tA 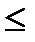 t
t 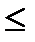 tB, т. е. 0
tB, т. е. 0 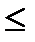 t
t 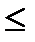 1, тогда dx=dy=dz=dt и
1, тогда dx=dy=dz=dt и

Пример: вычислите работу силового поля  вдоль параболы y=x2 от точки (0; 0) до точки (1; 1).
вдоль параболы y=x2 от точки (0; 0) до точки (1; 1).
|
|
|

т. к. y=x2, то dy=2xdx

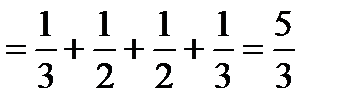
Пример: вычислите работу силового поля  вдоль контура треугольника ABC, если вершины треугольника имеют координаты: А(1; 0; 0); B(0; 1; 0); C(0; 0; 1).
вдоль контура треугольника ABC, если вершины треугольника имеют координаты: А(1; 0; 0); B(0; 1; 0); C(0; 0; 1).

Т. к. треугольник ограничен тремя разными прямыми линиями, то работа будет равна сумме работ, совершаемых вдоль отрезков, т. е. А=A1+A2+A3, где А1 – работа, вдоль прямой AB; А2 – работа вдоль ВС; А3 – работа вдоль CA. Вычислим работу вдоль линии AB. Находим канонические и параметрические уравнения всех трех прямых. Найдем каноническое уравнение прямой АВ и соответствующее ему параметрическое уравнение:
 ;
; 
т. е. x=-t+1; y=t; z=0; dx=-dt; dy=dt; dz=0
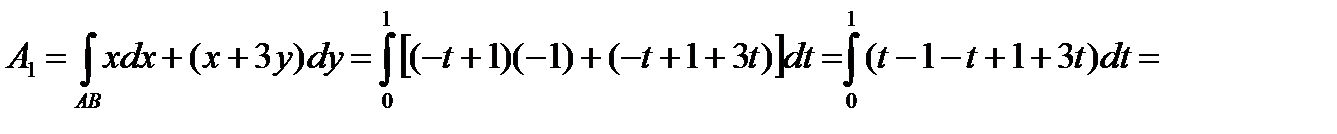

Вычислим работу вдоль линии BC. Найдем каноническое уравнение прямой линии ВС и соответствующее параметрическое уравнение прямой:
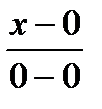 =
=  =
= 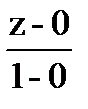 ;
; 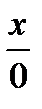 =
= 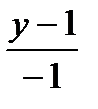 =
= 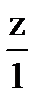 =t,
=t,
тогда x=0; y=-t+1; z=t; dx=0; dy=-dt; dz=dt


Вычислим работу вдоль прямой СА. Найдем каноническое уравнение прямой СА и соответствующее параметрическое уравнение:
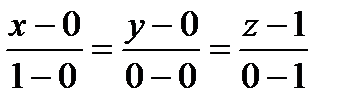 ;
; 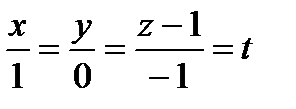
тогда х=t; y=0; z=-t+1; dx=dt; dy=0; dz = -dt

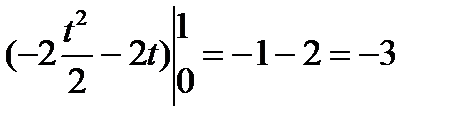

|
|
|


