 |
2.6. Формула Грина. 3. Поверхностный интеграл второго рода.. 3.1. Свойства поверхностных интегралов второго рода.
|
|
|
|
2. 6. Формула Грина.
Для достаточно общего вида плоских областей D с положительно ориентированной границей Г справедлива формула Грина:
(2. 10)
Формула Грина позволяет вычислить криволинейный интеграл второго рода по замкнутой линии Г, т. е. циркуляцию через двойной интеграл по области D, ограниченной этой кривой линией.
Пример: вычислить циркуляцию вектора
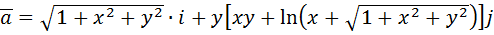
по окружности 
Циркуляция данного вектора равна:
Находим частные производные:
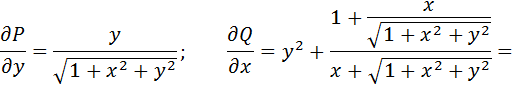
Тогда по формуле Грина (2. 10):
Т. к. кривая L является окружностью, то при вычислении двойного интеграла используем полярную систему координат: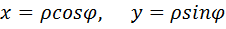 
Тогда
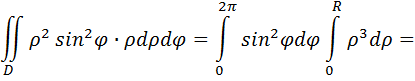
Пример: пользуясь формулой Грина, вычислить линейный интеграл в векторном поле 
где L- верхняя часть полуокружности 
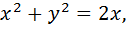направление обхода контура от точки A(2; 0) до точки О(0; 0)
Уравнение окружности: 
или 
т. е. центр окружности рис. 2. 4
сдвинут по оси Ох вправо на одну единицу. Дополним дугу полуокружности отрезком прямой ОА. Кривая ОАО – становится замкнутой.
Тогда по формуле Грина (2. 10):
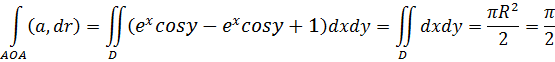
По свойству двойного интеграла полученный интеграл равен площади области D, а радиус полуокружности R=1. Интеграл вдоль прямой ОА равен нулю (на ОА у=0; dy=0), следовательно, окончательный ответ - линейный интеграл равен 
.
3. Поверхностный интеграл второго рода.
Пусть S – двухсторонняя ограниченная поверхность, заданная уравнением z = f(x, y), где f(x, y) – непрерывная функция в замкнутой области D – проекции поверхности S на плоскость XOY, а R(x, y, z) – непрерывная функция на поверхности S. Выберем верхнюю сторону поверхности S.
|
|
|
Разобьем поверхность S сетью кусочно-гладких линий на n частей Δ S1, Δ S2, …, Δ Sn. Проекциями этих линий на плоскость XOY область D разобьется на n областей, обозначим их соответственно Δ σ 1, Δ σ 2, …, Δ σ n. Возьмем на каждой части Δ Si произвольную точку Mi(ξ i, η i, ζ i) и составим интегральную сумму:
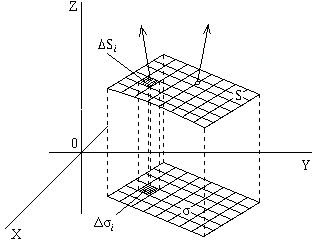
рис. 3. 1
Так как сторона поверхности выбрана верхняя, то (Δ Si)xy = Δ σ i, а значит
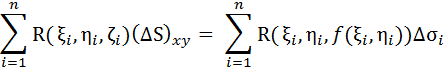
В правой части равенства имеем интегральную сумму для двойного интеграла от непрерывной функции R(x, y, f(x, y)) по области Dxy.
При стремлении к нулю шага разбиения поверхности S, Δ σ i также стремится к нулю. В пределе получаем формулу
(3. 1)
определяющую интеграл по верхней стороне поверхности S по переменным x и y через двойной интеграл по ее проекции на плоскость XOY.
Аналогичным образом устанавливается справедливость формул:
(3. 2)
для функции P(x, y, z), непрерывной на двухсторонней поверхности S, заданной уравнением x = f (x, y) (Dyoz – проекция поверхности S на плоскость YOZ) и
(3. 3)
для функции Q(x, y, z), непрерывной на двухсторонней поверхности S, заданной уравнением y = f (x, z).
Если поверхность S такова, что для функций P(x, y, z), Q(x, y, z) и R(x, y, z), определенных в точках этой поверхности, интегралы (3. 1), (3. 2) и (3. 3) существуют, то вводится понятие поверхностного интеграла «общего» вида по выбранной стороне поверхности:
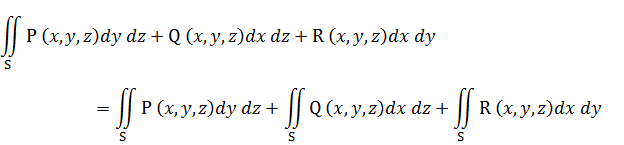
3. 1. Свойства поверхностных интегралов второго рода.
А) При перемене стороны поверхности S знак поверхностного интеграла второго рода меняется на противоположный.
Б) Постоянный множитель можно выносить за знак поверхностного интеграла:
|
|
|
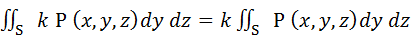
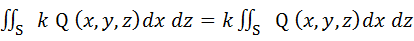
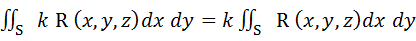
В) Поверхностный интеграл от суммы двух функций равен сумме соответствующих интегралов слагаемых:
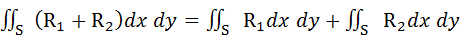
Г) Если поверхность S разбита на части S1 и S2, то интеграл по всей поверхности S равен сумме интегралов по ее частям:
Д) Если S – цилиндрическая поверхность с образующими, параллельными оси OZ, то
Если S – цилиндрическая поверхность с образующими, параллельными оси OX, то
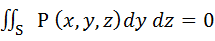
Если S – цилиндрическая поверхность с образующими, параллельными оси OY, то
|
|
|
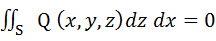
