4. Формула Стокса. Приложения. Варианты индивидуальных заданий. Выше мы уже определили понятие ротора вектора  как векторного произведения символического вектора набла =  +  +  и

4. Формула Стокса

Формула Стокса связывает криволинейный и поверхностный интегралы второго рода.

Пусть в некоторой области пространства задано поле непрерывно дифференцируемого вектора

 =P(x, y, z)  +Q(x, y, z)  +R(x, y, z)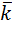

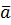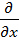
Выше мы уже определили понятие ротора вектора  как векторного произведения символического вектора набла =  +  +  и

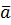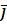вектора поля  =P  +Q  +R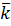

 

Тогда по формуле Стокса:

                                                                                              (4. 1)

Циркуляция вектора по любому замкнутому контуру L равна потоку ротора этого вектора через любую поверхность G, натянутую на контур L.

Предполагается, что ориентация нормали 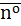 к поверхности G согласована с ориентацией контура L таким образом, чтобы из конца нормали обход контура в выбранном направлении был виден совершающимся против часовой стрелки. Формулу Стокса можно трактовать как обобщение формулы Грина для пространственного случая. В координатной форме формула Стокса имеет вид:

 

Формула Стокса позволяет вычислять криволинейные интегралы второго рода по замкнутым контурам с помощью поверхностных интегралов второго рода.

Пример: вычислить циркуляцию вектора  y  +x²  –z 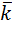  по контуру 

L:  x² +y² =4  при z=3; вычисления провести двумя способами:

а) непосредственно; б) по формуле Стокса.

x² +y² =4 – круговой цилиндр, радиуса R=2 с образующей, параллельной оси  OZ. Контур L - окружность, лежащая в плоскости z=3.

Выберем ориентацию дуги L как указано        на рис. 4. 1.

а) Параметрические уравнения линии L:

x= 2cos t;  y=2sint;  z=3; 0 ≤ t ≤ 2π

dx= -2sint dt; dy= 2cost dt;  dz=0

 

Вычисляем криволинейный интеграл второго рода. Тогда:

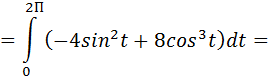
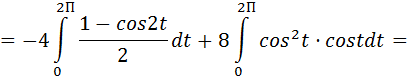
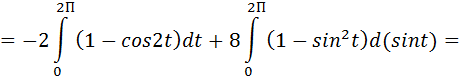
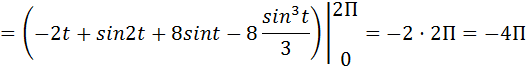
б) Вычисления по формуле Стокса начнем с определения ротора векторного поля:

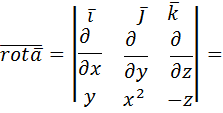
Вектор нормали к плоскости z=3 (0; 0; 1)

 Тогда, по формуле Стокса:

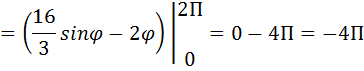
При вычислении интеграла воспользовались полярными координатами (x=ρ cos , y =ρ sin 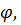 якобиан равен ρ ).

Пример: найти циркуляцию векторного поля  y  +z  +x 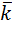 по окружности, получающейся при пересечении сферы x²+y²+z²=1, наклонной плоскостью  x+y+z=0, нормаль направлена в сторону положительной оси ОХ.  Плоскость x+y+z=0  полностью определяется своей нормалью ,

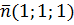длина нормали 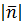= , тогда единичная нормаль, сонаправленная с данной имеет координаты .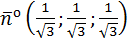

Вычислим ротор векторного поля в соответствии с формулой (2. 7):

    

Вычислим скалярное произведение ротора вектора поля и единичной нормали:

 

Следовательно, по формуле Стокса (4. 1):

 

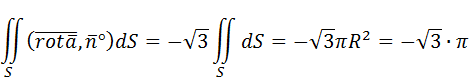
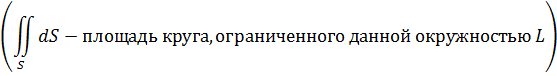
Приложения.

Варианты индивидуальных заданий.

Вариант № 1.

1) Вычислить потенциальную функцию векторного поля.

 

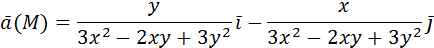
2) Вычислить работу векторного поля силы Ғ (М) при движении материальной точки по  заданному пути L:  

 

 

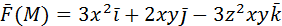
L: ломаная ABCD, AC // OX, CD // OX, DB // OY.

A (0, 1, 2), B (1, -1, 3)

3) Вычислить поток векторного поля через заданную поверхность в указанном направлении:

 

Поверхность замкнутая, нормаль внешняя.

 

Вариант № 2.

1) Вычислить потенциальную функцию векторного поля.

 

 

2) Вычислить работу векторного поля силы Ғ (М) при движении материальной точки по заданному пути L:

 

 

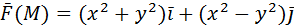
От точки M (2, 0) до точки N (0, 0).

 

3) Вычислить поток векторного поля через заданную поверхность в направлении внешней нормали.

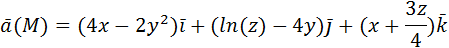
Вариант № 3.

 

1) Вычислить потенциальную функцию векторного поля.

 

 

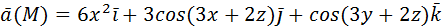
2) Вычислить работу векторного поля силы Ғ (М) при движении материальной точки по заданному пути L:

 

 

L: замкнутый контур, полученный пересечением поверхности

    координатными плоскостями.

 

3) Вычислить поток векторного поля через заданную замкнутую поверхность в сторону внешней нормали.

 

 

 

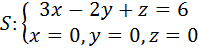
⇐ Предыдущая123456789Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: