Государственное образовательное учреждение высшего 3 страница

Необходимо определить имеется ли взаимосвязь между систолическим давлением и возрастом.

Решение. Создайте рабочую таблицу в Excel. Введите в ячейку А1 слово “Возраст”. Затем в ячейки А1: А12 – соответствующие значения возраста. В ячейку В1 введите “Систолическое давление”. В ячейки               В1: В12 – значения систолического давления. Затем вычисляется значение коэффициента корреляции между выборками. Установите курсор в свободную ячейку (А13). Нажмите кнопку Вставка функции (f_x) на панели инструментов. Выберите в диалоговом окне Мастер функций статистические функции, затем выберите функцию КОРРЕЛ.

Появится диалоговое окно КОРРЕЛ. Указателем мыши введите диапазон данных “Возраст” в поле массив 1 (А2: А12). Диапазон данных “Систолическое давление” введите в поле массив 2 (В2: В12).

В ячейке А13 после нажатия кнопки ОК появится значение коэффициента корреляции – 0, 61. Если проверить значимость коэффициента корреляции между переменными X и  при уровне значимости a=0, 05 (при n=20 t_кр. =2, 1), то можно сделать вывод, что имеется заметная линейная корреляционная связь между  и X.

 

                        Регрессионный анализ.

 

Регрессионный анализ устанавливает формы зависимости между случайной величиной Y (зависимой) и значениями одной или нескольких переменных величин (независимых), причем значения последних считаются точно заданными. Такая зависимость обычно определяется некоторой математической моделью (уравнением регрессии), содержащей несколько неизвестных параметров.

Приведем уравнения регрессии Y на X и X на Y:

M(Y)_x=f(x),   M(X)_y=j(y),

M(Y)_x – условное математическое ожидание величины Y, соответствующее значению x;

M(X)_y – условное математическое ожидание величины X, соответствующее значению y.

В результате n независимых опытов получены n пар чисел (x₁, y₁), (x₂, y₂), …, (x_n, y_n).

Найдем по данным наблюдений выборочное уравнение прямой линии регрессии.

Выборочное уравнение линейной регрессии Y на X будем искать в виде

                                                                                       (*)

Угловой коэффициент прямой линии регрессии Y на X называют выборочным коэффициентом регрессии Y на X.

Подберем параметры r_yx и b так, чтобы сумма квадратов отклонений ординат всех эмпирических точек от ординат соответствующих точек прямой (*) должна быть минимальной (в этом состоит сущность метода наименьших квадратов).

В результате применения метода наименьших квадратов получим следующие формулы для вычисления r_yx и b:

 ;

,

где , ,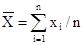

, ,

,

.

Линейный регрессионный анализ заключается в подборе графика и его уравнения для набора наблюдений.

Для получения коэффициентов уравнения регрессии используется процедура Регрессия из пакета анализа. Кроме того, могут быть использованы функция ЛИНЕЙН для получения параметров регрессионного уравнения и функция ТЕНДЕНЦИЯ для получения предсказанных значений Y в требуемых точках.

Для реализации процедуры Регрессия необходимо:

- выполнить команду Сервис, Анализ данных;

- в появившемся диалоговом окне Анализ данных в списке Инструменты анализа выбрать строку Регрессия;

- в появившемся диалоговом окне задать Входной интервал Y. Для этого необходимо, нажав левую кнопку мыши, протянуть указатель мыши от верхней ячейки столбца зависимых данных к нижней ячейке, затем отпустить левую кнопку мыши;

- указать Входной интервал X. Для этого необходимо, нажав левую кнопку мыши, протянуть указатель мыши от верхней ячейки столбца независимых данных к нижней ячейке, затем отпустить левую кнопку мыши;

- указать выходной диапазон. Для этого следует навести указатель мыши в положение Выходной интервал и щелкнуть левой кнопкой, навести указатель мыши на правое поле ввода Выходной интервал и щелкнуть левой кнопкой мыши, затем указатель мыши навести на левую верхнюю ячейку выходного диапазона и щелкнуть левой кнопкой мыши. Размер выходного диапазона будет определен автоматически;

- если необходимо проверить отличие экспериментальных точек от предсказанных по регрессионной модели, следует установить флажок в поле График подбора;

- нажать кнопку ОК.

Результаты анализа. Выходной диапазон будет включать в себя результаты дисперсионного анализа, коэффициенты регрессии, стандартную погрешность вычисления Y, среднеквадратичные отклонения, число наблюдений, стандартные погрешности для коэффициентов.

Приводимое значение R – квадрат (коэффициент детерминации) в регрессионной статистике определяет, с какой степенью точности полученное регрессионное уравнение аппроксимирует исходные данные. Если R – квадрат > 0, 95, говорят о высокой точности аппроксимации. Если R – квадрат лежит в диапазоне от 0, 8 до 0, 95, говорят об удовлетворительной аппроксимации. Если R – квадрат < 0, 6, то точность аппроксимации недостаточна и модель требует улучшения.

В таблице Дисперсионный анализ оценивается общее качество полученной модели: ее достоверность по уровню значимости критерия Фишера – p, который должен быть меньше, чем 0, 05. Значение p определяем в строке Регрессия, в столбце Значимость F.

Значения коэффициентов модели определяются из таблицы в столбце коэффициенты – в строке Y – пересечение приводится свободный член; в строках соответствующих переменных приводятся значения коэффициентов при этих переменных. В столбце p – значение приводится достоверность отличия соответствующих коэффициентов от нуля. В случаях, когда p > 0, 5, коэффициент может считаться нулевым. Это означает, что соответствующая независимая переменная практически не влияет на зависимую переменную и коэффициент может быть убран из уравнения.

Пример. Изучали зависимость между объемом Y (мкм³) и диаметром X (мкм) сухого эритроцита у млекопитающих. Результаты наблюдений приведены в таблице:

 

X	Y
7, 6
8, 9
5, 5
9, 2
3, 5
4, 8
7, 3
7, 4
6, 8

Необходимо на основании этих данных построить регрессионное уравнение.

Решение.

1. В пункте меню Сервис выберите строку Анализ данных

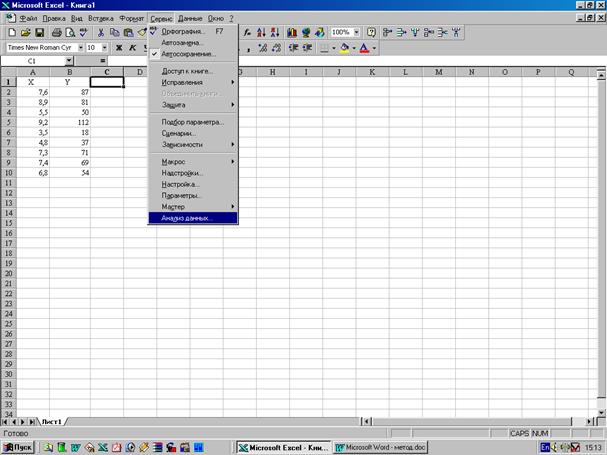
 и далее укажите курсором мыши на строку Регрессия.

2. В появившемся диалоговом окне задайте Входной интервал Y.

3. Укажите Входной интервал X.

4. Установите флажок в поле График подбора.

5. Укажите выходной диапазон. Для этого поставьте переключатель в положение Выходной интервал, затем наведите указатель мыши на правое поле ввода Выходной интервал  и, щелкнув левой кнопкой мыши, указатель мыши наведите на левую верхнюю ячейку выходного диапазона (C1). Щелкните левой кнопкой мыши. Нажмите кнопку ОК.

Результаты анализа. В выходном диапазоне появятся следующие результаты и график подбора.

 

ВЫВОД ИТОГОВ
Регрессионная статистика
Множественный R	0, 94943
R-квадрат	0, 901418
Нормированный R-квадрат	0, 887335
Стандартная ошибка	9, 446213
Наблюдения
Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия		5711, 383	5711, 383	64, 00676	9, 11E-05
Остаток		624, 6166	89, 23094
Итого
	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%	Нижние 95, 0%	Верхние 95, 0%
Y-пересечение	-32, 4752	12, 50339	-2, 59731	0, 035564	-62, 041	-2, 90936	-62, 041	-2, 90936
Переменная X 1	14, 28322	1, 785308	8, 000422	9, 11E-05	10, 06164	18, 5048	10, 06164	18, 5048
ВЫВОД ОСТАТКА
Наблюдение	Предсказанное Y	Остатки
	76, 07731	10, 92269
	94, 6455	-13, 6455
	46, 08255	3, 917447
	98, 93047	13, 06953
	17, 51611	0, 483886
	36, 0843	0, 915701
	71, 79235	-0, 79235
	73, 22067	-4, 22067
	64, 65074	-10, 6507

 

В таблице Дисперсионный анализ оценивается общее качество полученной модели: ее достоверность по уровню значимости критерия Фишера (строка Регрессия, столбец Значимость F, в примере 0, 0000911, то есть p=0, 0000911 и модель значима).

Приводимое значение R – квадрат (коэффициент детерминации) в регрессионной статистике определяет степень точности описания моделью процесса. В примере R – квадрат=0, 9015. Так как R – квадрат < 0, 95, не можем говорить о высокой точности аппроксимации.

Определим значения коэффициентов модели. На пересечении строки Y – пересечение и столбца Коэффициент приводится свободный член. В строке Переменная X1 приводится коэффициент при X1.

Поэтому выражение для определения объема сухого эритроцита у млекопитающих от диаметра будет иметь вид:

 

 

 

Однофакторный дисперсионный анализ.

 

 Для сравнения нескольких средних пользуются дисперсионным анализом. На практике дисперсионный анализ применяют, чтобы установить, оказывает ли существенное влияние некоторый качественный фактор А, который имеет m уровней А_1, А₂ … А _m  на изучаемую величину Х. Например, если требуется выяснить, какая доза рентгеновского излучения наиболее эффективно влияет на темп размножения бактерий, то фактор А – рентгеновское излучение, а его уровни – дозы излучений.

 Основная идея дисперсионного анализа состоит в сравнении факторной дисперсии и остаточной дисперсии. В математической статистике доказывается, что факторная дисперсия характеризует влияние фактора А на величину Х, а остаточная – влияние случайных причин.

Рассмотрим случай, когда число испытаний на различных уровнях различно. Пусть произведено q₁ испытаний на уровне А₁, q₂ испытаний на уровне А₂, …, q _m   испытаний – на уровне А_m.

Общую сумму квадратов отклонений наблюдаемых зачений от общей средней х находят по формуле:

 

S_общ = [P₁ + P₂ + …+ P_m] – (R₁ +R₂ +… + R_m)²/n,

 где

P₁ = 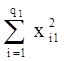- сумма квадратов наблюдавшихся значений признака на уровне А₁;

 

P₂ = - сумма квадратов наблюдавшихся значений признака на уровне А₂;

                  _{. . .}

 

P_m = - сумма квадратов наблюдавшихся значений признака на уровне А _m.

 

R₁ = , R₂ = … R_m =  - суммы наблюдавшихся значений признака соответственно на уровнях А_1, А_{2, …} А_m.

 

n= q_{1 +} q_{2 +… +}q_m - общее число испытаний ( объем выборки).

 

Факторную сумму квадратов отклонений групповых средних от общей средней, которая характеризует рассеяние " между группами" находят по формуле:

 S_{факт =} [ ( R₁²/q₁) + (R₂²/q₂ ) +… + (R_m²/q_m )] – [ (R₁ + R₂ + …+ R_m)² /n]

 

 Остаточную сумму квадратов отклонений наблюдаемых значений группы от своей групповой средней, которая характеризует рассеяние " внутри групп", находят по формуле:

S _ост = S _общ -S _факт

Факторную дисперсию находят по формуле:

 

S² _факт = S _факт / (m-1)

 Остаточную дисперсию находят по формуле:

 S² _ост = S _ост /(n-m)

 

Сравниваем факторную и остаточную дисперсии.

 Если факторная дисперсия окажется меньше остаточной, то фактор не оказывает существенное влияние на величину Х.

Если факторная дисперсия больше остаточной, то применяем критерий Фишера - Снедекора, для чего найдем наблюдаемое значение критерия

 F _набл = S² _факт / S² _ост

 

 По таблице “Критические точки распределения F Фишера - Снедекора” находим критическую точку F_кр ( ά; m-1; n-m), ά – уровень значимости. Если F  _набл  > F_кр, то гипотезу о равенстве групповых средних отвергаем, значит фактор А оказывает существенное влияние на величину Х.

Для проведения в MS Excel дисперсионного анализа необходимо:

- ввести данные в таблицу. В каждом столбце должны быть данные, соответствующие одному значению исследуемого фактора. Столбцы должны располагаться в порядке возрастания (убывания) величины исследуемого фактора;

- выбрать команду Сервис, затем Анализ данных в списке Инструменты анализа выбрать процедуру Однофакторный дисперсионный анализ;

-  в появившемся диалоговом окне задать Входной интервал, то есть таблицу данных;

- в разделе Группировка переключатель установить в положение по столбцам;

- указать выходной диапазон, то есть ввести ссылку на ячейки, в которые будут выведены результаты анализа.

 

Пример.  

Определить достоверность влияния фермента (фактора А) на выход продукта биохимического синтеза при уровне значимости a£ 0, 05.

№ испытания	Уровни фактора А     А1                   А2                 А3                             А4
1      2      3	70     74     69	67      70      66	67     71     76	70     67     68

Результаты анализа.

В результате будет получена таблица

Однофакторный дисперсионный анализ
ИТОГИ
Группы	Счет	Сумма	Среднее	Дисперсия
Столбец 1
Столбец 2			67, 66667	4, 333333
Столбец 3			71, 33333	20, 33333
Столбец 4			68, 33333	2, 333333
Дисперсионный анализ
Источник вариации	SS	df	MS	F	P-Значение	F критическое
Между группами	30, 91667		10, 30556	1, 212418	0, 366066	4, 06618
Внутри групп			8, 5
Итого	98, 91667

В таблице Дисперсионный анализ на пересечении строки Между группами и столбца MS находится значение факторной дисперсии 10, 30556. На пересечении строки Внутри групп и столбца MS находится значение остаточной дисперсии 8, 5. Наблюдаемое значение критерия Фишера – Снедекора равно 1, 212418. F критическое 4, 06618. F_набл. < F_кр. , следовательно фактор А не оказывает существенное влияние на величину X.

 

                                   Контрольная работа

№	Часть 1			Часть 2
	1	2	3	1	2	3	4
	1. 1		1, 2, 3	1	2	3	4
	2. 2		4, 5, 6
	3. 3		7, 8, 9
	4. 2		10, 11, 12
	5. 3		13, 14, 15
	6. 2		16, 17, 18
	7. 1		19, 20, 21
	8. 1		3, 5, 22
	9. 2		7, 9, 11
	10. 1		13, 14, 17
	11. 1		19, 20, 22
	12. 2, 12. 3		2, 4, 6
	13. 3		8, 10, 12
	14. 4		14, 16, 18
	15. 4		2, 20, 22
	16. 2		3, 6, 9
	17. 1		12, 15, 18
	18. 2		4, 8, 12
	19. 1, 19. 2		7, 16, 20
	20. 2		1, 4, 7
	21. 2		10, 13, 16
	22. 1		5, 19, 22
	2. 2		2, 5, 8
	4. 1		11, 14, 17
	6. 3		11, 19, 20
	7. 3		1, 6, 11
	10. 2		7, 16, 21
	12. 1		2, 7, 12
	14. 3		1, 17, 22
	16. 3		3, 8, 13
	18. 1		1, 11, 18
	20. 1		4, 9, 14
	22. 2		9, 19, 21
	1. 2		5, 10, 15
	3. 2		6, 11, 17
	5. 3		1, 8, 15
	7. 2		2, 9, 16
	9. 4		3, 11, 19

Таблица вариантов Номер варианта выбирается по последним двум цифрам шифра.                                                        

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: