Рис. 9 Рис. 10

Рис. 9                                                            Рис. 10

 

Если объем Р больше (шире) объема S, то Р не распределен.

2-й случай. В суждении «Все квадраты — равносторонние прямо­угольники» термины такие: S — «квадрат», Р — «равносторонний пря­моугольник»; квантор общности — «все». В этом суждении S распреде­лен и Р распределен, так как их объемы полностью совпадают (рис. 10).

Если S равен по объему Р, то Р распределен. Это бывает в опреде­лениях и в выделяющих общих суждениях.

Суждение I — частноутвердительное. Его структура: «Некоторые 5 есть Р». Рассмотрим два случая.

1-й случай. В суждении «Некоторые подростки — филателисты» термины такие: S — «подросток», Р — «филателист»; квантор существо­вания — «некоторые». Соотношение 5 и Ризображено на рис. 11. Субъект не распределен, так как в нем мыслится только часть подростков, т. е. объем субъекта лишь частично включается в объем предиката. Предикат тоже не распределен, так как он также лишь частично включен в объем субъек­та (только некоторые филателисты являются подростками).

S — подрос- А Р — фи-
ток Илателист

Рис. 11

Если понятия 5 и Р перекрещиваются, то Р не распределен.

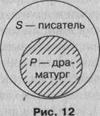
2-й случай. В суждении «Некоторые писатели — драматурги» термины такие: S — «писатель», Р — «драматург»; квантор существо­вания — «некоторые». Субъект не распределен, так как в нем мыслит­ся только часть писателей, т. е. объем субъекта лишь частично включа­ется в объем предиката. Предикат распределен, так как объем предиката полностью входит в объем субъекта (рис. 12). Таким образом, Р рас­пределен, если объем Р меньше объема 5.

Такие суждения называются частновыделяющими и считаются исключением из общего правила распределенности терминов для част­ноутвердительных суждений.

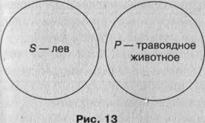
Суждение Е — общеотрицательное. Его структура: «Ни одно 5 не есть Р». Например, «Ни один лев не есть травоядное животное». В нем термины такие: 5 — «лев», Р — «травоядное животное»; кван- горное слово — «ни один». Здесь объем субъекта полностью исклю­чается из объема предиката, и наоборот. Поэтому и S, и Р распределе­ны (рис. 13).

 

Суждение О — частноотрицательное. Его структура: «Некото- I> ые Sне есть Р». Например, «Некоторые учащиеся не являются спортс­менами». В нем такие термины: S — «учащийся», Р — «спортсмен» и квантор существования — «некоторые». Субъект не ра спределен, так как мыслится лишь часть учащихся, а предикат распределен, ибо в нем м ыслятся все спортсмены, ни один из которых не включен в ту часть учащихся, которая мыслится в субъекте (рис. 14).

Итак, 5 распределен в общих суждениях и не распределен в част­ных; Р всегда распределен в отрицательных суждениях, в утвердитель­ных же он распределен тогда, когда по объему Р< S.

Распределенность терминов в категорических суждениях можно выразить в виде схемы, где знаком (+) выражена распределенность К'рмина, а знаком (-) его нераспределенность.

В ней же дана объединенная информация о простых суждениях.

Без знания правил распределенности терминов в категорических суждениях отпадает один из способов проверки правильности умоза­ключения.

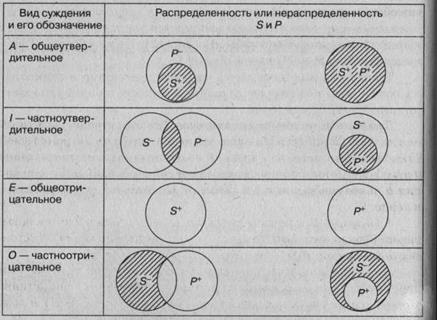
Рис. 15

 

§ 3 СЛОЖНОЕ СУЖДЕНИЕ И ЕГО ВИДЫ

Связи между простыми суждениями выражаются с помощью ло­гических терминов (союзов, связок): конъюнкции, дизъюнкции и дру­гих (о них речь пойдет ниже). Строя формулу сложного суждения или дедуктивного умозаключения, мы пользуемся средствами исчисления высказываний — одним из разделов математической (символической) двузначной логики. Напомним, что термины «суждение» и «высказы­вание» мы употребляем как синонимы с учетом того, что в традицион­ной логике (нематематической) употребляется термин «суждение», а в математической — термин «высказывание». Итак, сложные сужде­ния образуются из простых суждений с помощью логических связок: конъюнкции, дизъюнкции, импликации, эквиваленции и отрицания, которые приблизительно соответствуют союзам естественного языка «и», «или», «если..., то», «тогда и только тогда, когда... » и «неверно,

что... ». Если вопрос об истинности или ложности простых суждений решается путем обращения к действительности, то значение истинно­сти сложных суждений определяется с помощью таблиц истинности, где буквы а, Ь, с — переменные, обозначающие простые суждения; буква «и» обозначает истину, а «л» — ложь.

 

Таблицу истинности для конъюнкции (алЬ) можно разъяснить на следующем примере. «Сверкнула молния (а) и загремел гром (Ь)». Она будет истинна в том и только в том случае, если суждения а и b оба истинны. Это и отражено в первой строке. Если же а ложно или b ложно либо и а, и b ложны, то вся конъюнкция обращается в ложь.

Суждение «Увеличение рентабельности достигается путем повы­шения производительности труда (а) или путем снижения себестои­мости продукции (Ь)» — пример нестрогой дизъюнкции.

Дизъюнкция называется нестрогой, если ее члены не исключают друг друга. Такое высказывание истинно в том случае, если истинно хотя бы одно из двух суждений (первые три строки таблицы), и лож­но, если оба суждения ложны. Обозначается a v Ь.

Члены строгой дизъюнкции (a v b) исключают друг друга. Это мож­но разъяснить на примере: «Я поеду на юг на поезде (а) или полечу на самолете (Ь)»; «Я не могу одновременно ехать на поезде и лететь на самолете». Строгая дизъюнкция истинна тогда, когда истинно лишь одно из двух простых суждений.

Таблицу для импликации (а-^> Ь) можно разъяснить на таком при­мере: «Если через проводник пропустить электрический ток (а), то проводник нагреется (Ь)». Импликация истинна всегда, кроме одного случая: если первое суждение истинно, а второе ложно. Действитель­но, не может быть, чтобы по проводнику пропустили электрический юк, т е. чтобы суждение (а) было истинным, а проводник не нагрелся, । . е. суждение (Ь) было ложным.

Эквиваленция в таблице (а = Ь) характеризуется так: а = Ь истин­но в тех и только в тех случаях, когда и а, и b либо оба истинны, либо < > ба ложны.

Отрицание суждения а (т. е. а) характеризуется так: если а ис- । ннно, то его отрицание ложно, и если а ложно, то а истинно.

Если в формулу входят три переменных, то таблица истинности для этой формулы, включающая все возможные комбинации истин­ности или ложности ее переменных в таблице, будет состоять из 2³ = 8 строк, при четырех переменных в таблице будет 2⁴ = 16 строк; при пяти переменных в таблице имеем 2⁵ = 32 строки; при п переменных — 2” строк.

Алгоритм распределения значения «и» и «л» для переменных (на­пример, для четырех переменных a, b, с, d) таков:

а	ь	с	d
и и и и и и и и л л л л л л л л	и и и и л л л л и и и и л л л л	и и л л и и л л и и л л и и л л	И л и л и л и л и л и л и л и л

 

Имеем 2⁴ = 16 строк.

В столбце для а сначала пишем 8 раз «и» и 8 раз «л».

В столбце для b сначала пишем 4 раза «и» и 4 раза «л», затем по­вторяем и т. д.

Выполнимая формула та, которая может принимать по крайней мере одно значение «истина». Тождественно-истинной формулой на­зывается формула, которая при любых комбинациях значений для вхо­дящих в нее переменных принимает значение «истина» (иначе она называется законом логики, или тавтологией). Тождественно-ложная формула та, которая соответственно принимает только значение «ложь» (она иначе называется противоречием).

Приведем доказательство тождественной истинности двух фор­мул, одна из которых включает две переменные, а другая — три.

Возьмем формулу ((а —> Ь) лЬ) —> а. Таблица истинности для нее будет такой:

а	ь	а	ь	а—> Ь	(а—> £ > ) лЬ	((а-»Ь) л Ь)—> а
и	и	л	л	И	л	И
и	л	л	и	л	л	и
л	и	и	л	и	л	и
л	л	и	и	и	и	и

Так как в последней колонке мы имеем только значение «исти­на», формула является тождественно-истинной, или законом логики (такие выражения называют тавтологиями).

Рассмотрим таблицу истинности для формулы

((а Ь) л (а с) л (b v с)) —> а.

a	ь	с	а	ь	с	а-> Ь	а-*с	(b V с)	(а-> Ь) л л (а-»с) л А (Й V С)	л л (а-»с) л л (bvc))-> a
и	И	и	л	л	л	И	и	л	Л	И
и	и	л	л	л	и	и	л	и	Л	и
и	л	и	л	и	л	л	и	и	Л	и
и	л	л	л	и	и	л	л	и	Л	и
л	и	и	и	л	л	и	и	л	Л	и
л	и	л	и	л	и	и	и	и	и	и
л	л	и	и	и	л	и	и	и	и	и
л	л	л	и	и	и	и	и	и	И	и

 

Так как в последней колонке мы имеем только значение «исти­на», формула является тождественно-истинной, или законом логики.

Построение таблиц истинности потребуется в последующих гла­вах IV и V для того, чтобы, например, выявлять, будет ли в умозаклю­чении заключение следовать из посылок или нет, т. е. определять, бу­дет ли формула, соответствующая структуре этого умозаключения, законом логики или нет.

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: