§ 5. Сложные и сложносокращенные силлогизмы (полисиллогизмы, сориты)

Полисиллогизмом (сложным силлогизмом) называют два или несколько простых категорических силлогизмов, связанных друг с другом таким образом, что заключение одного из них становится посылкой другого. Различают прогрессивные и регрессивные поли-' силлогизмы.

В прогрессивном полисиллогизме заключение предшествующего силлогизма становится большей посылкой последующего силло­гизма.                                               <

Например:

Все продукты, содержащие витамины, способствуют жизнедеятельности организма.

Фрукты — продукты, содержащие витамины.

Значит, фрукты способствуют жизнедеятельности организма.

Яблоки сорта «Антоновка» — фрукты.

Яблоки сорта «Антоновка» способствуют жизнедеятельности организма.

Регрессивный полисиллогизм — это такой сложный силлогизм, в ко­тором заключение предшествующего силлогизма становится меньшей посылкой последующего силлогизма.

I. Все планеты — небесные тела. 2. Все небесные тела имеют массу.

Сатурн — планета.                              Сатурн — небесное тело.

Сатурн — небесное тело.                  Сатурн имеет массу.

Сорит (с общими посылками)

Прогрессивный и регрессивный полисиллогизмы в мышлении чаще всего применяются в сокращенной форме — в виде соритов.

Существуют два вида соритов: прогрессивный и регрессив­ный.

Прогрессивный сорит получается из прогрессивного поли­силлогизма путем выбрасывания заключений предшествующих сил­логизмов и больших посылок последующих.

Все, что укрепляет здоровье, полезно.

Спорт укрепляет здоровье.

Гимнастика — спорт.

Ритмическая гимнастика — вид гимнастики.

Ритмическая гимнастика полезна.

В прогрессивном сорите первая посылка содержит предикат за­ключения, а последняя посылка содержит субъект заключения.

Регрессивный сорит получается из регрессивного полисиллогизма путем выбрасывания заключений предшествующих силлогизмов и меньших посылок последующих. В первом категорическом силло­гизме меняем местами посылки:

Сатурн — планета.

Все планеты — небесные тела.

Все небесные тела имеют массу.

Сатурн имеет массу.

В регрессивном сорите первая посылка содержит субъект вы­ключения, а последняя посылка — предикат заключения.

§ 6. УСЛОВНЫЕ УМОЗАКЛЮЧЕНИЯ

Чисто условным умозаключением называется такое опосредован­ное умозаключение, в котором обе посылки являются условными суж­дениями. Условным называется суждение, имеющее структуру: «Если а, то Ь». Структура чисто условного умозаключения такая:

Если а, то Ь. Если Ь, то с.	Схема: а-^b, Ь-*с
Если а, то с.	а—м:

 

Этот вид умозаключения часто используется в школе, в частности на уроках математики, физики и др.

Приведем пример.

Если у ученика не воспитано уважение к добросовестному труду (а), то у него не выработается потребность трудиться (Ь).

Если у ученика не выработается потребность трудиться (Ь), то он не станет полноценным гражданином (с).

Если у ученика не воспитано уважение к добросовестному труду (а), то он не станет полноценным гражданином (с).

В чисто условном умозаключении существуют его разновидности (модусы). К ним относится, например, такой:

Если а, то Ь. Если не-а, то Ь.	Схема: а^> Ь а-> Ь
Ь	Ь

 

Формула: ((а—> 6) л (а-^Ь)) Ь.

Данная формула является законом логики, т. е. тождественно-ис­тинной формулой.

Примером такого умозаключения является следующее рас­суждение:

Если треугольник является равносторонним, то сумма его внутренних углов равна 180°.

Исли треугольник не является равносторонним, то сумма его внутрен­них углов равна 180°.

Сумма внутренних углов треугольника равна 180°.

Условно-категорические умозаключения

Условно-категорическое умозаключение — это такое дедуктивное умозаключение, в котором одна из посылок — условное суждение, а дру­гая — простое категорическое суждение. Оно имеет два правильных модуса, в которых заключение с необходимостью следует из посылок.

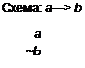I. Утверждающий модус.

Структура его: если а, то Ь.

а
b

Этой схеме соответствует формула (1): ((а -> Ь) л а)     Ь, которая

нвляется законом логики.

Можно строить правильные умозаключения от утверждения ос­нования к утверждению следствия.

Приведем два примера.

Если хочешь наслаждаться искусством, ты должен быть художествен­но образованным человеком.

Ты хочешь наслаждаться искусством.

Гы должен быть художественно образованным человеком.

Для построения другого примера воспользуемся интересным вы- сказыванием великого русского педагога К. Д. Ушинского: «Если человек избавлен от физического труда и не приучен к умственному, зверство овладевает им». Использовав это высказывание, построим условно-категорическое умозаключение.

Если человек избавлен от физического труда и не приучен к умствен­ному, то им овладевает зверство.

)тот человек избавлен от физического труда и не приучен к умственному.

)тим человеком овладевает зверство.

Любое использование правил в русском языке, математике, физи-/ ке, химии и других школьных дисциплинах основано на утверждающем модусе, дающем достоверное заключение, поэтому в практике мышле*- ния он находит самое широкое применение.

Если этот металл свинец, то он тяжелее воды.

Данный металл — свинец.

Данный металл тяжелее воды.

II. Отрицающий модус.

Структура его: если а, то Ь. Схема: а^Ь

He-b                 b

^Не2^а _ а

Формула (2): ((а-^b) лЬ)-ь а — также является законом логики.

Можно строить правильные умозаключения от отрицания след­ствия к отрицанию основания.

Приведем два примера.

Если река выходит из берегов, то вода заливает прилегающие терри­тории.

Вода реки не залила прилегающие территории.

Река не вышла из берегов.

Для построения второго условно-категорического умозаключения воспользуемся следующим высказыванием: «... тот мерзок, кто ярится, если чужой он доблести свидетель» (Данте Алигьери. Божественная комедия).

Умозаключение построено так:

Если человек при виде чужой доблести ярится, то он мерзок.

Этот человек не является мерзким.

Этот человек при виде чужой доблести не ярится.

Условно-категорическое умозаключение может давать не только достоверное заключение, но и вероятное.

Первый вероятный модус

Структура его: если а, то Ь.        Схема: а —> b

b                       b

Вероятно, а > Вероятно, а

Формула (3): ((а -> b) л Ь) -> а — не является законом логики.

Нельзя достоверно умозаключать от утверждения следствия к утверждению основания.

Люди иногда неправильно умозаключают так:

Если бухта замерзла, то суда не могут входить в бухту.

Суда не могут входить в бухту.

Бухта замерзла. (? )

Заключение будет лишь вероятным, т. е. вероятно, бухта замерз­ла; а возможно, дует сильный ветер, или бухта заминирована, или име­ется какая-либо другая причина.

Нельзя и так умозаключать:

Если данное тело — графит, то оно электропроводке.

Данное тело электропроводно.

Данное тело — графит. (? )

Второй вероятный модус

Структура его: если а, то Ь. Схема: а -> b

Не-а                       а

Вероятно, не-b Вероятно, Ъ

Формула (4): ((а -»Ь) л а) —> b — не является законом логики.

Нельзя достоверно умозаключать от отрицания основания к от­рицанию следствия.

Некоторые врачи рассуждают ошибочно:

Если человек имеет повышенную температуру, то он болен. Данный человек не имеет повышенной температуры.

Данный человек не болен.

§ 7. РАЗДЕЛИТЕЛЬНЫЕ УМОЗАКЛЮЧЕНИЯ

Разделительным называется умозаключение, в котором одна или несколько посылок — разделительные (дизъюнктивные) суждения. ( уществуют чисто разделительные и разделительно-категорические умозаключения.

В чисто разделительном умозаключении обе (или все) посылки являются разделительными суждениями.

В традиционной логике принята следующая его структура:

S есть А, или В, или С.                                                                                              / '

А есть или или Л₂.

S есть или Л„ или Л₂, или В, или С.

Пример

По типу силовой установки самолеты бывают или с поршневым двига­телем, или с газотурбинным двигателем.

Самолеты с газотурбинным двигателем имеют или турбовинтовой дви­гатель, или турбореактивный двигатель.

По типу силовой установки самолеты бывают или с поршневым двига- I телем, или с турбовинтовым двигателем, или с турбореактивным дви­гателем.

В разделительно-категорическом умозаключении одна посылка — I разделительное суждение, другая — простое категорическое суждение. Этот вид умозаключения содержит два модуса.

I модус — утверждающе-отрицающий.

Пример

Запоминания бывают произвольными или непроизвольными.

Данное запоминание было непроизвольным.

Данное запоминание не было произвольным.

В этом модусе союз «или» употребляется обязательно в смысле строгой дизъюнкции.

Ошибки происходят из-за смешения в этом модусе строгой и нестрогой дизъюнкции. Нельзя, например, рассуждать таким об- ч разом:

Учащиеся в контрольной работе по математике допускают или вычис­лительные ошибки, или ошибки в эквивалентных преобразованиях, 1 или в применении изученных алгебраических правил.

Учащийся Сидоров допустил в контрольной работе вычислительные ошибки.

Сидоров не допустил в работе ни ошибок в эквивалентных преобра­зованиях, ни ошибок в применении изученных алгебраических пра-; вил.                                              ,

Заключение не является истинным суждением, так как Сидоров мог допустить все три вида ошибок.

II модус — отрицающе-утверждающий.

Приведем примеры.

()тбор в живой природе бывает искусственным или естественным. Данный отбор не является искусственным.

Данный отбор является естественным.

Приведем второй пример рассуждения, построенного по отрица- юще-утверждающему модусу. Для этого воспользуемся рассказом • Пестрая лента» А. Конан Дойля, в котором он описал раскрытие страшного преступления — убийства девушки с помощью ядовитой змеи. III. Холмс рассказал Уотсону; «Вначале я пришел к совершенно неправильным выводам, мой дорогой Уотсон, и это доказывает, как опасно опираться на неточные данные. Присутствие цыган, слово „бан- la" ^[XIV], сказанное несчастной девушкой, — всего этого было достаточно, чтобы навести меня на ложный след. Но когда мне стало ясно, что в ком­нату невозможно проникнуть ни через дверь, ни через окно, что не от­туда грозит опасность обитателю этой комнаты, я сразу понял свою ошибку, и это может послужить мне оправданием. Как я уже говорил нам, внимание мое сразу привлекли вентилятор и шнур от звонка, ви­сящий над кроватью. Когда обнаружилось, что звонок фальшивый, а кровать прикреплена к полу, у меня сразу зародилось подозрение, ч го шнур служит лишь мостом, соединяющим вентилятор с кроватью. Мне сразу пришла мысль о змее, а зная, как доктор любит окружать себя всевозможными индийскими тварями, я понял, что, пожалуй, на­пал на верный след. Именно такому хитрому, жестокому злодею, про­бившему много лет на Востоке, могло прийти в голову употребить яд, который нельзя обнаружить химическим путем».

Разделительно-категорическое умозаключение было построено III. Холмсом таким образом:

(> битателю комнаты грозила опасность проникновения в комнату или через дверь, или через окно, или через вентилятор.

В комнату невозможно проникнуть ни через дверь, ни через окно».

11 комнату можно проникнуть через вентилятор.

В разделительной посылке должны быть предусмотрены все возможУ ные альтернативы, т. е. деление должно быть полным. Это правило обяза­тельно для данного отрицающе-утверждающего модуса, и Ш. Холмс это правило выполнил, сформулировав все возможные способы проникно­вения в комнату.

Приведем другой пример.

Пожар мог произойти или в результате небрежного обращения с ог­нем, или в результате поджога, или по причине неисправной электро­проводки.

Данный пожар не произошел ни в результате небрежного обращения с огнем, ни по причине неисправной электропроводки.

Данный пожар произошел в результате поджога.

Заключение здесь не достоверное, а вероятное, так как в первой разделительной посылке перечислены не все возможные причины воз­никновения пожара (например, в результате взрыва или в результате загорания от молнии и т. д. ).

§ 8. УСЛОВНО-РАЗДЕЛИТЕЛЬНЫЕ (ЛЕММАТИЧЕСКИЕ)
УМОЗАКЛЮЧЕНИЯ

Условно -разделительное умозаключение — это такое дедуктивное умозаключение, в котором одна посылка состоит из двух или более условных суждений, а другая является разделительным суждением. В зависимости от числа членов в разделительной посылке это умоза­ключение может быть дилеммой (если разделительная посылка содер­жит два члена) или вообще полилеммой (если в разделительной по­сылке три и более членов деления).

Дилемма

Дилеммы бывают двух видов: конструктивные и деструктивные; обе формы дилеммы, в свою очередь, могут быть простыми и сложными.

Простая конструктивная дилемма

Состоит из двух посылок. В первой утверждается, что из двух раз» личных оснований вытекает одно и то же следствие. Во второй, которая является дизъюнктивным суждением, утверждается, что одно или дру­гое из этих оснований истинно. В заключении утверждается следствие.

Приведем пример простой конструктивной дилеммы. В роману В. Шукшина «Я пришел дать вам волю» написано так: «Давай думать, как быть. Две дороги домой: Кумой или Волгой. Обои закрыты. Там и тут надо пробиваться силой. Добром нас никакой дурак не пропустит. А раз такое дело, давай решим: где легче? » Простая конструктивная дилем­ма представлена в такой форме:

Нели плыть Кумой (а), то надо пробиваться силой (Ь); если плыть Волгой (с), то надо пробиваться силой (Ь).

Можно плыть Кумой (а), или Волгой (с).

11адо пробиваться силой (Ь).

Малыми буквами а, Ь, с обозначаются простые суждения. Знак • v» обозначает строгую дизъюнкцию, т. е. возможна только одна из двух альтернатив, так как одновременно плыть и Кумой, и Волгой нельзя. Запись а-+Ь обозначает «если а, то Ь». Соединив посылки знаком «л» (конъюнкция, соответствующая союзу «и») и присоединив к ним по­средством знака «—> » заключение, мы получим формулу этого вида ди­леммы:

((а —> Ь) л (с —> Ь) л (a v с)) —> Ь.

Эта формула является законом логики, т. е. тождественно-истин­ной формулой.

Возьмем второй пример. Врач точно не установил, какого рода гравма у больного, поэтому перед ним стоит дилемма:

I ели у больного растяжение (а), то следует назначить парафинную процедуру (Ь); если у больного ушиб (с), то также следует назначить парафинную процедуру (Ь).

У данного больного растяжение связок (а) или ушиб (с).

Данному больному следует назначить парафинную процедуру (Ь).

Запись a v h обозначает «а или Ь» (нестрогую дизъюнкцию), так как и растяжение связок, и ушиб могут быть одновременно.

Формула этой дилеммы: ((а Ь) л (с —> Ь) л (a v с)) Ь.

Сложная конструктивная дилемма

В первой посылке имеются два основания, из которых вытекают соответственно два следствия; во второй посылке, которая представ­ок д собой дизъюнктивное суждение, утверждается истинность одно- |о или другого основания; в заключении утверждается истинность од­ного или другого следствия. Сложная конструктивная дилемма и сличается от простой только тем, что следствия ее условной посылки различны, а не одинаковы.

Этот вид дилеммы значительно чаще встречается в мышлении людей, в сознании литературных героев, исторических деятелей, по­этому мы приведем пример из художественной литературы.

Татьяна Тэсс в рассказе «Поединок в море» (из книги «Неви­димый свидётель») описывает такую ситуацию: «Танкер „Ростов" взял около десяти тысяч тонн автомобильного бензина и уже гото­вился в Туапсе к отплытию... Сейчас танкер должен сняться с яко­ря... Якорь уже вышел из воды... На лапе якоря висит авиабомба, пролежавшая на дне моря двадцать лет. Капитан танкера „Ростов" Александр Котляров думал не только о своем судне, а и о других танкерах, тоже залитых бензином и нефтью, стоящих неподалеку от причалов. „Сколько времени пройдет, пока из Севастополя в Ту­апсе придут минеры? Бомба может взорваться каждую минуту. Двадцать лет она пролежала под водой, а сейчас может взорваться от любой случайности" ».

Перед капитаном встала очень тяжелая дилемма:

Если я оставлю танкер в порту до прибытия минеров, то бомба мо­жет взорваться и повредить много судов; если я уведу танкер в море, то в случае взрыва пострадает только один танкер.

Я могу оставить танкер в порту до прибытия минеров или увести в море.

Может пострадать много судов в порту или в случае взрыва пострада­ет только один танкер.

Капитан принимает такое решение: немедленно, не дожидаясь прибытия из Севастополя минеров, уйти из порта в море. Уйти, чтобы обезопасить другие суда, отплыть на такое расстояние, чтобы в случае взрыва опасность грозила бы только одному его танкеру. Уйти в море и там утопить бомбу. Танкер ушел из порта, и со второй попытки бом­бу удалось утопить в море, а танкер не пострадал.

Формула этой дилеммы такая:

((а-ь b) л (с d) л (av с)) —» (b v d).

Простая деструктивная дилемма

В ней первая (условная) посылка указывает на то, что из одного и того же основания вытекают два различных следствия. Во второй посылке содержится дизъюнкция отрицаний обоих этих следствий. В заключении отрицается основание.

Формула этой дилеммы такая;

((а -» Ь) л (а -» с) л (Ъ v с)) —> а.

Герой романа Т. Драйзера «Американская трагедия» Клайд раз­мышляет, что если он женится на Роберте, то его ждет «скучное, буд­ничное существование в заботах о том, как прожить с нею и с ребенком па скудный заработок», что женитьба для него «означала бы полный крах». Выразим рассуждение Клайда в форме дилеммы:

Рели я женюсь на Роберте, то меня ждет скучное существование и для меня наступит полный крах.

Я не хочу влачить скучное существование или потерпеть полный крах.

Я не женюсь на Роберте.

Сложная деструктивная дилемма

Она отличается от простой только тем, что оба основания ее раз- шчны. Первая посылка содержит два условных суждения с различ­ными основаниями и различными следствиями. Во второй посылке содержится дизъюнкция отрицаний обоих следствий. Заключение яв- шется дизъюнкцией отрицаний обоих оснований.

Формула: ((а Ь) л (с -> d) л (Ъ v d) -> (a v с).

Приведем пример этого вида дилеммы.

I ели человек пунктуален, то он всегда приходит вовремя на встречу । другим человеком; а если человек вежлив, то, опоздав, всегда изви­нится.

Данный человек или не всегда приходит вовремя на встречу с другим человеком, или не извиняется, когда опаздывает.

В другом рассказе Л. Толстого «Акула» речь идет о том, что два мальчика с корабля, стоявшего у берегов Африки, купались в откры­том море. «Вдруг с палубы кто-то крикнул: „Акула! " — и все мы увиде­ли в воде спину морского чудовища. Акула плыла прямо на мальчи­ков». Артиллерист, отец одного из мальчиков, услышав их визг, «сорвался с места и побежал к пушкам. Он повернул хобот, прилег к пушке, прицелился и взял фитиль. Мы все, сколько нас было на ко­рабле, замерли от страха и ждали, что будет. Раздался выстрел, и мы увидели, что артиллерист упал подле пушки и закрыл лицо руками... по волнам колыхалось желтое брюхо мертвой акулы».

Столь же напряженка и драматична ситуация, описанная Л. Тол­стым в рассказе «Прыжок». Мальчик вслед за обезьянкой забрался на мачту, затем «он пустил веревку и ступил на перекладину, покачи­вая руками; все замерли от страха. Стоило ему только оступиться — и он бы вдребезги разбился о палубу... В это время капитан корабля, отец мальчика, вышел из каюты. Он нес ружье, чтобы стрелять чаек. Он увидел сына на мачте и тотчас же прицелился в сына и закричал:

— В воду! Прыгай сейчас в воду! Застрелю!

Мальчик шатался, но не понимал.

— Прыгай или застрелю!

Раз, два... — и как только отец крикнул: „три" — мальчик размах­нулся головой вниз и прыгнул.... Секунд через сорок — они долго по­казались всем — вынырнуло тело мальчика. Его схватили и вытащили на корабль. Через несколько минут у него изо рта и из носа полилась вода, и он стал дышать».

Дилеммы сформулированы и в других рассказах из книг для чте­ния. В рассказе «Честное слово» Л. Пантелеева мальчик в игре дал чест ное слово стоять на посту, а ребята ушли, забыв о нем, и мальчик ока зался поздно вечером один в саду, и только военный смог заставить мальчика «оставить пост». Н. Артюхова в рассказе «Большая береза» описала переживания и поведение матери, увидевшей, какая опасность грозит сыну, взобравшемуся на большую березу: «Она смерила глаза­ми расстояние от его ветки до земли, и лицо у нее стало почти такое же белое, как этот ровный березовый ствол».

Рассказ А. Гайдара «Совесть» начинается так: «Нина Карнаухо­ва не приготовила урока... и решила не идти в школу».

Решение дилемм, т. е. выбор одной из двух стоящих перед челове­ком альтернатив, проходит иногда в острой борьбе, требующей мгно­венной реакции на ситуацию, и всегда связано с моральными качества­ми личности. Детские рассказы, включающие дилеммы, помогают воспитывать такие черты характера, как совесть, ответственность, по­рядочность, обязательность и др. Такова же роль сказок и басен. 11з двух зол выбирай наименьшее, решай дилемму честным способом.

Студентам I курса МП ГУ было предложено найти дилеммы в дет­ской литературе. Студентка Антонова Анна, которая только что окон­чила Московское педучилище № 15, где в течение двух лет изучала курс «/(стекая литература», смогла привести 15 примеров дилемм из дет­ской литературы. Предлагаем читателю самостоятельно найти и сфор­мулировать дилеммы, пользуясь приведенным ниже списком ли- гературы, составленным А. Антоновой.

1. Носов Н. Мишкина каша. М., 1977. С. 3.

2. Андерсен Г. Х. Дикие лебеди // Сборник сказок. Минск, 1986. С. 283.

3. Андерсен Г. Х. Свинопас // Там же. С. 274.

4. Шарль Перро. Рикки с хохолком // Там же. С. 9.

5. Толстой А. Приключения Буратино (две дилеммы) // Луко­морье. Сказки русских писателей. М„ 1969. С. 476, 487.

6. Киплинг Р. Маугли (несколько дилемм) // Сборник сказоч­ных повестей. М., 1985. С. 22, 48.

7. Гайдар А. Чук и Гек. Сочинения. М.; Л., 1948. С. 359.

8. Лагин Л. Старик Хоттабыч. Магадан, 1973. С. ПО.

9. Волков А. Семь подземных королей // Сказочные повести. М., 1992. С. 249.

10. Волков А. Желтый туман // Там же. С. 460.

Студентка I курса Мельникова Лена, только что закончившая музыкально-педагогическое училище, тоже привела много примеров дилемм из детской литературы. Вот несколько книг из тех, что предла- । лет Лена.

1. Андерсен Г. Х. Дюймовочка // Сказки, истории. М., 1973. С. 49.

2. Шварц Н. Сказка о потерянном времени. Цветик-семицветик // < казки советских писателей. М., 1991. С. 184.

3. Милн Алан. Винни-Пух и все-все-все. М., 1985. С. 490.

4. Стивенсон Р. Л. Остров сокровищ. Л., 1977. С. 16.

5. Золушка. Сказки народов Югославии. М., 1991. С. 185.

6. Лагин Л. Старик Хоттабыч. М„ 1973. С. 146.

Трилемма

Трилеммы так же, как и дилеммы, могут быть конструктивными И деструктивными; каждая из них может быть простой или сложной.

В сложной конструктивной трилемме первая посылка состоит и । । рех различных оснований и трех различных вытекающих из них след- । гний, т. е. содержит три условных суждения. Вторая посылка является

дизъюнктивным суждением, в котором утверждаются основания. В за­ключении (дизъюнктивном суждении) утверждаются следствия.

В некоторых сказках говорится о надписях на перекрестках трех дорог, которые содержат в себе, например, такого рода трилемму:

Кто поедет прямо, будет в холоде и голоде; кто поедет направо, тот сам останется цел, а конь будет убит; кто поедет налево, тот сам будет убит, а конь останется цел.

Человек может поехать либо прямо, либо направо, либо налево.

Он или будет в холоде и голоде, или сам останется цел, а конь будет убит, или сам будет убит, а конь останется цел.

Приведем пример трилеммы периода Второй мировой войны.

В своих воспоминаниях «Ладожский экзамен» Л. И. Баркович пи­шет об истории Ладожской дороги, которая свидетельствовала о му­жестве и настойчивости защитников Ленинграда. Ладожская дорога, «Дорога жизни», была фронтом. Направляясь в Ленинград по Ладож­скому озеру, Иван Игнатьевич Баркович, будучи шофером грузовой машины, взял С собой сына Леонида, так как вторую машину — полу­торку — вести было некому. В автоколонне сын двигался за машиной отца. Дорога была опасна. Враг держал ее под огнем, лед расходился, образуя просветы. Вдруг машина отца остановилась — оказалось, кон­чился бензин.

Леонид Баркович рассуждает:

«У моей машины горючее тоже было на исходе. Переливать по­ловину оставшегося бензина в бак отцовского „газика" было глупо — горючее могло кончиться раньше, чем мы добрались бы до берега.

Поехать вперед, сообщить, что тут стоит машина? Но помощь может прийти поздно...

Взять на буксир его машину — лед мог не выдержать». Леони, принял решение: «Давай трос! На буксире у меня пойдешь! » Добра лись благополучно.

Приведенная трилемма военных лет показывает героизм, мужест во, находчивость и преданность защитников Родины.

Найдите примеры дилемм и трилемм в художественной литератур» Опишите ситуацию, в которой происходит действие, затем четко сфо[ мулируйте дилемму (трилемму), проанализируйте, какую из альтерн; тив принял человек и каким оказался результат его решения.

В математике структура трилеммы используется тогда, когда во никают три возможных варианта решения задачи, доказательства те< ремы и предстоит выбор одного из них.

Деструктивные трилеммы так же, как и деструктивные дилем­мы, бывают простыми и сложными. Структура их аналогична струк­туре дилеммы, только предусматриваются не две, а три возможные альтернативы.

§ 9. СУЩНОСТЬ И ВИДЫ ИНДУКЦИИ

Зная, что при соблюдении правил построения дедуктивного умо- 1аключения истинные посылки приводят к истинным результатам, естественно поставить вопрос: «Как убедиться в истинности посы- юк? » Эти посылки могут быть получены с помощью дедуктивных умозаключений из других посылок. А как получены другие посыл­ки? В итоге мы приходим к таким положениям, которые дедуктивно ни из каких иных положений не выводятся. Из каких посылок мож­но вывести, например, такие заключения: «Все тела движутся», • Все тела притягиваются друг к другу» и т. д.? Здесь нужно опирать­ся на факты, приводя примеры движущихся, тяготеющих друг к дру- । у тел. К фактам приходится прибегать и тогда, когда дедуктивный нывод в принципе возможен, но истинность посылок труднее обосно­вать, чем истинность заключения. Например, пусть нам надо дока­зать свое алиби, обосновав положение о том, что в тот день, когда было совершено преступление, мы не выходили из дома. Если при­знать истинным суждение о том, что мы всю неделю не выходили из дома, то отсюда дедуктивно следовало бы, что и во вторник на этой педеле мы не выходили из дома. Однако более общее суждение обосно- пать труднее. Поэтому достаточно сослаться на факты, относящиеся пппь ко вторнику: нам звонили утром, заходили днем, видели в окно вечером и т. д.

Ссылка на факты обычно считается убедительной, но часто приво­дит... к неверным результатам. Любители детективных сюжетов знают, что на первый взгляд бесспорное, казалось бы, обоснованное фактами алиби может быть ложным: преступник успевает совершить преступле­ние за тот маленький отрезок времени, когда за ним никто не наблюда- | | Или другой пример: мы видим много движущихся тел, но еще боль­шее количество мы не видим, а значит, не можем их наблюдать. Правомерно ли в таком случае утверждение: «Все тела движутся? » В этих и подобных случаях, хотя все известные факты достоверны, ошибочный вывод не исключен, потому что мы выходим за пределы све­дений, содержащихся в посылках. Умозаключения, в которых вывод рас­ширяет сферу знания, выраженного в посылках, называются индуктив­ны ни, или просто индукцией.

С точки зрения строгой логической теории дедуктивного вывода индуктивные умозаключения по большей части являются неправиль­ными, поскольку в них не гарантируется достоверность получаемого результата. Однако существует большая разница не только между ис­тинными и ложными суждениями, но и между суждениями более ве­роятными и менее вероятными. Например, возьмем два суждения: «Завтра на улице будет тепло» или «Завтра на улице будет холодно». Оба они проблематические. Кто знает, какая завтра будет погода? Но если сейчас зима, то одно из них — «Завтра на улице будет холод­но» — более вероятно, хотя нет никакой гарантии, что не наступит отте­пель. Поэтому выяснение условий повышения вероятности вывода имеет не меныпес практическое значение, чем формулирование правил, при выполнении которых эти выводы будут безусловно достоверными.

Достоверное заключение дает полная индукция, т. е. умозаключе­ние, в котором общее заключение о некотором классе предметов дела­ется на основании изучения всех предметов этого класса. Так как в пол­ной индукции мы не выходим за рамки того, что было дано в посылках, ее иногда вообще не считают индуктивным умозаключением. Более правильно было бы сказать, что полная индукция является своеобраз­ной комбинацией индуктивного умозаключения (от частного к об­щему) с дедукцией из посылки, в которой утверждается, что исчерпа­ны все частные случаи. Но и здесь мы не застрахованы от ошибки в том случае, если некоторые представители интересующего нас класса про­сто неизвестны. Например, раньше астрономы делали ошибочный вы вод, что все планеты и спутники движутся в одном направлении пото­му, что ученым еще не были известны спутники самых отдаленных от Солнца планет, которые движутся в другом направлении.

Полная индукция часто применяется в математических и других строгих доказательствах. Математическая индукция — метод доказа­тельства математических утверждений, основанный на принципе: утверждение А(х), зависящее от натурального параметра х, считается доказанным, если доказано А(1) и для любого натурального п из пред^[XV] положения, что верно А(п), выведено, что верно также А(п + I)¹.

Кроме полной и математической индукции в науке, обучени и обыденной жизни, мы часто встречаемся с неполной индукцией, К( торая по способам обоснования заключения делится на три вида:

1) индукция через простое перечисление (популярная); 2) инду1 ция через анализ и отбор фактов; 3) научная индукция. Рассмотрим пе| вый и третий вид неполной индукции. К последней относится индукци через перечисление. Суть этого вида индукции заключается в том, что на основании повторяемости одного и того же признака у ряда однород­ных предметов и отсутствия противоречащего случая делается общее заключение, что все предметы этого рода обладают этим признаком. Гак, известно, что люди не бессмертны, они умирают. Но сколько было людей в прошлом и сколько будет в будущем? Кто может ответить па этот вопрос? А сколько всего звезд, молекул, физических тел? Давая ответ, мы ссылаемся на бесконечность, представить которую невозмож­но. И тем не менее это не мешает нам верить в то, что все тела притяги­ваются друг к другу. Но даже и в этом случае можно сформулировать условия, при выполнении которых вывод, полученный индуктивным пу­тем, будет более правдоподобным.

1. Число случаев, зарегистрированных в посылках, должно быть возможно большим. Однако это условие само по себе не всегда сущест­венно. Существует рассказ о мореплавателе, который говорил королю Сиама невероятные глупости о своей стране, и король всему верил. 11о когда мореплаватель впервые сказал правду, что зимой у них вода । гановится твердой и по ней можно ходить и ездить, король обвинил его во лжи. Дело в том, что король исходил из своих наблюдений, наблюдений своих подданных и жителей соседних стран. Поскольку никто из них не видел, чтобы вода становилась твердой, они не могли поверить мореплавателю. Мы видим, что причина заключается не в не­достаточном количестве фактов, а в том, что все они носят однотип­ный характер. Таким образом, нарушено второе, более существенное, чем первое, условие правдоподобия индуктивного вывода.

2. Факты, на основе которых делается вывод, должны быть как можно более разнообразными. Падение яблока на землю и движение Луны вокруг Земли настолько разнородные явления, что до Ньюто­на никому не приходило в голову их объединить для получения вы­вода: «Все тела притягиваются друг к другу». Именно разнородность н их фактов обеспечивала высокую степень достоверности получен­ного вывода. Способность увидеть связь разнообразных фактов, вый- | -| за рамки привычного стереотипа, — вот признак творческого мыш- Н’НИЯ.

3. Рассматриваемые факты должны быть типичными, существен­ными. Например, желая доказать, что вода в море соленая, нельзя про­бовать ее в Рижское заливе и в Черном море около Одессы весной, потому что вода там не обладает существенным, типичным признаком морской воды — соленостью. Балтийское море — бывшее пресновод­ное озеро, а в Одесском заливе вода весной опресняется за счет павод- h. i рек, таких, как Днепр и Дунай.

Необходимо отметить, что между третьим и вторым условиями существует некоторое противоречие. Нужно исходить из компромис­са между обоими требованиями: стараться брать разнообразные при­меры, где бы содержались типичные, существенные признаки рассмат­риваемых явлений.

Научная индукция на основе установления причинной связи

Научной индукцией называется такое умозаключение, в котором на основании познания необходимой связи признаков части предметов класса делается общее заключение обо всех предметах этого класса. На­учная индукция так же, как полная индукция и математическая индук­ция, дает достоверное заключение. Достоверность (а не вероятность) за­ключений научной индукции, хотя она охватывает и не все предметы изучаемого класса, а лишь их часть (и притом небольшую), объясняется тем, что учитывается важнейшая из необходимых связей — причинная. С помощью научной индукции делается заключение: «Всем людям для их жизнедеятельности необходима влага». В частности, Ю. С. Николаев и Е. И. Нилов в книге «Голодание ради здоровья» пишут, что человек без пищи (при полном голодании) может прожить 30—40 дней, а воду он дол­жен пить ежедневно: без воды человек не может жить, ибо процесс обеэ! воживания организма ведет к нарушению внутриклеточного обмена ве­ществ, что приводит к гибели человека. Голодание же, наоборот, при многих заболеваниях (например, хроническом нефрите, гипертонической болезни, стенокардии, атеросклерозе, нейродермите, бронхиальной астме, общем ожирении и многих других) способствует выздоровлению, в частя ности при одноразовом или повторном длительном голодании. Этот вы­вод был тоже получен путем научной индукции.

Причиной йзлечивания этих болезней при длительном голодании является изумительная саморегуляция организма во время полного лечебного голода, когда осуществляется общебиологическая пере­стройка организма больного. Обычное переедание, которое ежеднев| но задает о

⇐ Предыдущая567891011121314Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: