§ 4 выражение логических связок (логических постоянных)

§ 4 ВЫРАЖЕНИЕ ЛОГИЧЕСКИХ СВЯЗОК (ЛОГИЧЕСКИХ ПОСТОЯННЫХ)

В ЕСТЕСТВЕННОМ ЯЗЫКЕ

Логические связки в естественном языке (русском) выражаются различным образом.

Конъюнкция (знак «л») выражается союзами «и», «а», «но», «да», ♦ хотя», «который», «зато», «однако», «не только..., но и» и др. В логике высказываний знак «л» соединяет простые суждения, образуя из них (•ложные. В естественном языке союз «и» и другие слова, соответству­ющие конъюнкции, могут соединять существительные, глаголы, наре­чия, прилагательные и другие части речи. Например: «В корзине у деда чежали подберезовики и маслята» (а л Ь); «Интересная и красиво оформленная книга лежит на столе». Последнее суждение нельзя раз­бить на два простых, соединенных конъюнкцией: «Интересная книга «ежит на столе» и «Красиво оформленная книга лежит на столе», так как создается впечатление, что на столе лежат две книги, а не одна. Тогда это одно простое суждение.

В логике высказываний действует затон коммутативности конъ юнкции (а л Ь) = (Ь л а). В естественном русском языке такого закона нет, так как действует фактор времени. Поэтому не будут эквивалент ными, например, такие два суждения:

1. «Прицепили паровоз, и поезд тронулся» и 2) «Поезд тронулся и прицепили паровоз».

В естественном языке конъюнкция может быть выражена не толь ко словами, но и знаками препинания: запятой, точкой с запятой, тире

В естественном (русском) языке дизъюнкция (обозначенная av b и a v Ь) выражается союзами «или», «либо», «то ли... то ли» и др. На пример: «Вечером я пойду в кино или в библиотеку»; «... Через несколь ко дней мы окажемся перед хорошеньким выбором: либо придется от править на виселицу ни в чем не повинного человека, либо Британска империя полетит в преисподнюю» (Г. К. Честертон).

Приведем логические схемы и соответствующие им примеры иллюстрирующие разнообразные способы выражения импликации.

2. Если А, то В.

Если поставщики вовремя доставят детали, завод выполнит сво производственный план.

3. Коль скоро А, то В.

Коль скоро приложенные силы снимаются, то сжатая пружина возвращается к своей первоначальной форме.

4. Когда А, имеет место В.

Когда наступает плохая погода, имеет место повышение числ сердечно-сосудистых заболеваний у людей.

5. Для В достаточно А.

Для того чтобы газы расширились, достаточно их нагреть.

6. Для А необходимо В.

Для сохранения мира на земле необходимо объединить усили всех государств в борьбе за мир.

7. А, только если В.

Старшеклассники этого класса не приходили на занятия, тольк если они были больны.

8. В, если А.

«Империи обращались в прах, если в них начинала рушиться се мья... » (В. Астафьев).

Приведем логические схемы и соответствующие им примеры раз нообразных способов выражения эквиваленции.

1. А, если и только если В.

Иванов не закончит cbqh эксперименты к сроку, если и тольк если ему не помогут сотрудники.

2. Если Л, то В, и наоборот.

Если при равномерном движении скорость увеличивается в два раза, то за то же время движения пройденный путь удваивается, и на­оборот.

3. А, если В, и В, если А.

Многоугольник является вписанным в круг, если его вершины к'жат на окружности, и вершины многоугольника лежат на окружно­сти, если этот многоугольник является вписанным в круг.

4. Для А необходимо и достаточно В.

Для того чтобы число без остатка делилось на 3, необходимо и до­статочно, чтобы сумма цифр этого числа делилась без остатка на 3.

5. А равносильно В (иногда).

То, что площадь правильного многоугольника равна произ­ведению полупериметра на апофему, равносильно тому, что площадь правильного многоугольника равна произведению периметра на по­ловину апофемы.

6. Атогда и только тогда, когда В.

Фирма будет согласна принять предложение о покупке товара тогда и только тогда, когда цена этого товара будет снижена на 18%.

Из приведенных выше схем и соответствующих им высказываний । конкретным разнообразным содержанием становится ясно, насколь­ко многогранны в естественном языке (в частности, в русском) сред- । тиа выражения импликации, эквиваленции и других логических свя-.! < ж (логических терминов). Это можно сказать и о других естественных языках^[VIII].

Импликация (а —> Ь) не совсем соответствует по смыслу союзу ■ ■ если... то» естественного языка, так как в ней может отсутствовать содержательная связь между суждениями а'и Ь.

Кроме логических связок, для выражения общих и частных суж­дений в логике используются квантор общности и квантор существо­вания. Запись с квантором общности Х/хР(х)обычно читается так: «Все । (из некоторой области объектов) обладают свойством Р», а запись । квантором существования ЗхР(х) читается: «Существуют такие х (и данной области), которые обладают свойством Р». Например, Зх(х > 100) читается как «Существуют такие х, которые больше 100», где иод х подразумеваются числа. В русском языке квантор общности выражается словами: «все», «всякий», «каждый», «ни один» и др. Кван-

тор существования выражается словами: «некоторые», «существуют» «только некоторые», «не все», «немногие» и др.

В практике математических и иных рассуждений имеются поня тия «необходимое условие» и «достаточное условие». Условие назы вается необходимым, если оно вытекает из заключения (следствия)

Условие называется достаточным, если из него вытекает заключение (следствие). В импликации а —> b переменная а называется основани ем, или антецедентом. Переменная b — следствием, или консеквентом Ниже предлагаются задачи, требующие в каждом из следующих предложений вместо многоточия поставить слова: «необходимо» или «достаточно» либо «необходимо и достаточно».

1. Для того чтобы сумма двух целых чисел была четным числом.. чтобы каждое слагаемое было четным.

2. Для того чтобы число делилось на 15... чтобы оно делилось на 5

3. Для того чтобы произведение (х - 3) (х + 2) (х - 5) было равно 0... чтобы х = 3.

4. Для того чтобы четырехугольник был прямоугольником... что бы все его углы были равны.

§ 5. ОТНОШЕНИЯ МЕЖДУ СУЖДЕНИЯМИ
ПО ЗНАЧЕНИЯМ ИСТИННОСТИ

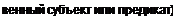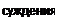Суждения, как и понятия, делятся на сравнимые (имеют тождест­делятся на совместимые и несовместимые.

В математической логике два простых высказывания р и q назы­ваются несовместимыми, если из истинности одного из них необходи мо следует ложность другого (т. е. р и q не могут оказаться одновре­менно истинными).

Простые совместимые суждения выражают одну и ту же мысл] полностью или лишь в некоторой части. Отношения совместимости эквивалентность, логическое подчинение, частичное совпадение (суб­контрарность ).

Простые эквивалентные суждения выражают одну и ту же мысл! в различной форме («Юрий Гагарин — первый космонавт» и «Юриг Гагарин первым полетел в космос»). Субъект здесь один и тот же, а пре­дикаты — тождественные понятия. Если два суждения эквивалентны то невозможно, чтобы одно из них было истинным, а другое ложным.

Простые совместимые суждения, находящиеся в отношении ло­гического подчинения, имеют общий предикат;, понятия, выражающие субъекты двух таких суждений, могут находиться в отношении логи-

веского подчинения или быть тождественными понятиями. Отноше­ния между суждениями по истинности принято схематически изобра­жать в виде «логического квадрата».

Противоположность

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: