Решение. Пример 1.2. Вычислить разность двух комплексных чисел: . Пример 1.2. Вычислить разность двух комплексных чисел:

Решение.

Из приведенных примеров видно, что формулы (1. 1) и (1. 2. ) помнить необязательно. Сложение и умножение комплексных чисел можно выполнять по правилам сложения и умножения двучленов.

Разность двух комплексных чисел – операция обратная сложению и может быть выполнена по формуле:            (1. 3).

Пример 1. 2. Вычислить разность двух комплексных чисел:

Решение

Из приведенного примера видно, что формулу (1. 3) помнить необязательно. Вычитание комплексных чисел можно выполнять по правилам вычитания двучленов

Число 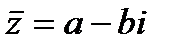 называется комплексно-сопряженным с комп­лексным числом . Понятие комплексной сопряженности взаимно.

Сумма и произведение комплексно-сопряженных чисел со­ответственно равны 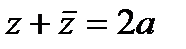 и .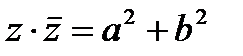

Частное от деления одного комплексного числа на второе – операция обратная умножению и может быть выполнена по формуле:

      (1. 4)

 Эту формулу можно не запоминать, а руководствоваться следующим правилом:  для того, чтобы разделить одно комплексное число на другое, надо записать их в виде дроби, в числителе которой – делимое, а в знаменателе – делитель, а затем числитель и знаменатель умножить на число, сопряженное со знаменателем.

Покажем справедливость этого правила:

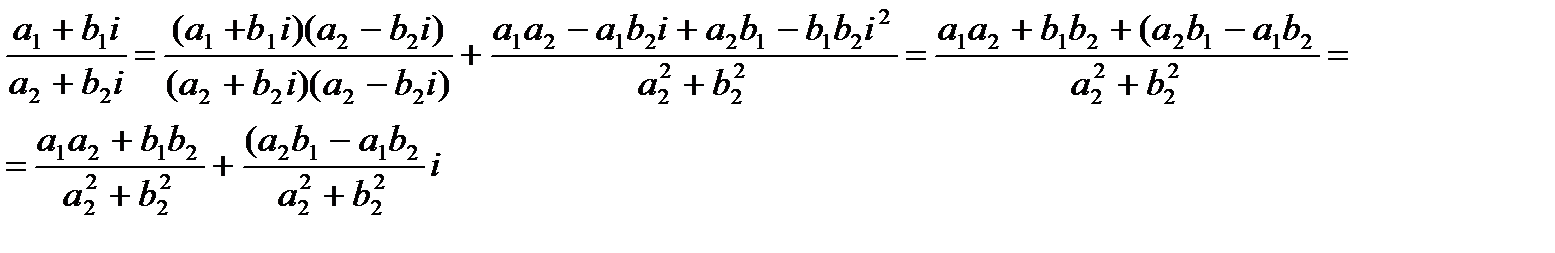
Как можно увидеть, получившееся в результате использования приведенного выше правила деления комплексных чисел совпадает с правой частью формулы (1. 4), что свидетельствует о справедливости этого правила.

Пример 1. 3.

Вычислить частное от деления комплексного числа на комплексное число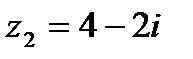

Решение

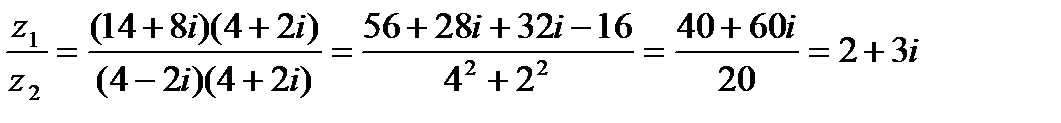
В этом примере использованы по сути те же данные, что и во втором из примеров 1. 1. В данном случае делимое – результат перемножения комплексных чисел примера 1. 1. Делитель – второй из сомножителей упомянутого примера. Частное от деления в текущем примере совпало с первым сомножителем примера 1. 1., что подтверждает правильность выполненной нами операции деления.

Комплексное число равно нулю тогда и только тогда, ког­да.

Для комплексных чисел, так же, как и для векторов, нет по­нятия больше и меньше.

Покажем, как в множестве комплексных чисел решаются квадратные уравнения, дискриминанты которых меньше нуля.

Пусть, например, нужно решить уравнение 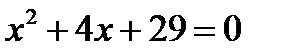. Легко подсчитать, что

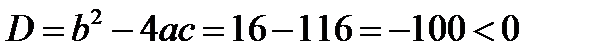
Сле­довательно,

.

Поэтому

То есть, квадратное уравнение с действительными ко­эффициентами и отрицательным дискриминантом имеет два комплексно-сопряженных корня.

Операция возведения в степень комплексного числа рассмат­ривается как частный случай произведения одного и того же со­множителя.

Степени мнимой единицы даются формулой

Например,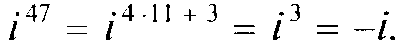  

Пример 1. 4. Найти действительные числа х и yиз уравнения

Решение. Используем условия равенства двух комплексных чисел  и .

Пользуясь определени­ем суммы, получаем 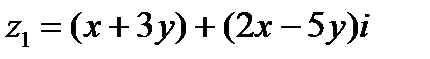 Сравнивая действите­льные и мнимые части чисел z₁ и z₂, получим систему двух урав­нений относительно х и у , решением которой будет .

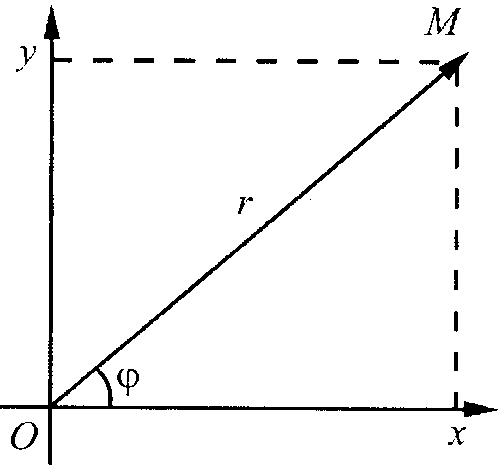
1. 2. Геометрическая интерпретация комплексных чисел

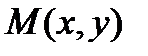На координатной плоскости Оху любая точка М задается абс­циссой х и ординатой у: . Но эта же точка, если она отлична от начала координат, может быть задана и полярными ко­ординатами  и . Декартовы координаты могут быть вычислены через полярные координаты следующим образом:

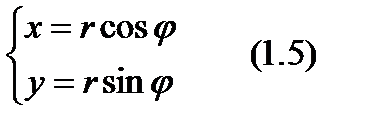
По Декартовым координатам можно вычислить полярные координаты точки:

Точке М(0; 0) соответствует r = 0;  не определен.

Пример 1. 5. В полярной системе координат постройте точки: .

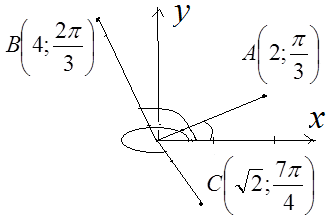Решение.

Пример 1. 6.  Найдите полярные координаты точек, симметричных с точками

а) относительно полюса б) относительно полярной оси.

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: