 |
2.3.Участки выпуклости и вогнутости кривой. Общая схема исследование функции и построения ее графика
|
|
|
|
2. 3. Участки выпуклости и вогнутости кривой. Общая схема исследование функции и построения ее графика
л Построение графика
Непрерывная линия называется выпуклой или обращенной выпуклостью вверх на отрезке [а, b], если все точки этой линии лежат выше хорды, соединяющей любые две ее точки.
Вогнутой (обращенной выпуклостью вниз) называется линия, проходящая ниже своих хорд.
Замечание. В некоторых руководствах выпуклость и вогнутость иногда определяются противоположным образом.
Точки, отделяющие выпуклые участки линии от вогнутых (и наоборот), называются точками перегиба.

|
Теорема. Если вторая производная функции 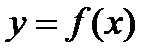 в данном промежутке значений х положительна:
в данном промежутке значений х положительна:
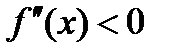 (2. 10),
(2. 10),
то кривая вогнута в этом промежутке, а если отрицательна:
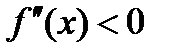 (2. 11),
(2. 11),
то кривая в этом промежутке выпукла.
Точками перегиба являются те точки, при переходе через которые вторая производная меняет знак.
Линия является выпуклой (или вогнутой ) в точке, если значение ее второй производной в данной точке меньше (или больше) нуля.
Пример. 2. 9. Выяснить, выпуклая или вогнутая линия  при
при 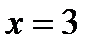 .
.
Решение. Находим производные  . В точке
. В точке 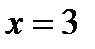 имеем:
имеем:  . Значит, в точке
. Значит, в точке  данная линия вогнута.
данная линия вогнута.
Нахождение точки перегиба. Чтобы исследовать функцию на вогнутость, необходимо определить знак второй производной. Если на данном промежутке f" (х) < 0 для всех х, то линия вогнута, если f" (х) > 0 для всех х, то линия выпукла. Выпуклую часть кривой от вогнутой отделяет точка перегиба.
|
|
|
Чтобы найти точку перегиба линии  :
:
1. Найти вторую производную функции  .
.
2. Приравняв ее к нулю, решить полученное уравнение.
3. Расположив корни второй производной  . в порядке возрастания, подставить в выражение для второй производной сначала любое число, меньшее
. в порядке возрастания, подставить в выражение для второй производной сначала любое число, меньшее  , затем - любое число
, затем - любое число 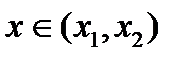 ; если получатся разные знаки, то при
; если получатся разные знаки, то при 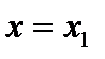 имеется точка перегиба; если же одинаковые, то точки перегиба нет; далее аналогично поступить с числами
имеется точка перегиба; если же одинаковые, то точки перегиба нет; далее аналогично поступить с числами  .
.
4. Найти ординаты точек перегиба, т. е. найти значения функции в соответствующих точках.
Пример 2. 10. Найти точки перегиба линии  .
.
Решение . Находим: 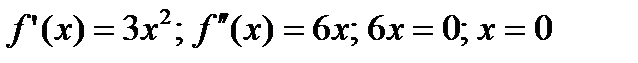 .
.
Разобьем числовую прямую на интервалы: 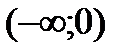 ;
; 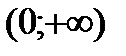 .
.
Определим знак второй производной в каждом из интервалов.
| x | 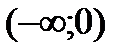
| 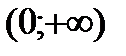
|

| - | + |
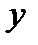
| выпуклая | вогнутая |
При переходе через 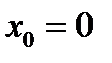 вторая производная меняет знак на противоположный, следовательно, при
вторая производная меняет знак на противоположный, следовательно, при  линия имеет перегиб.
линия имеет перегиб.
Ординату точки перегиба определим, подставив 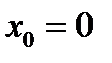 в уравнение линии:
в уравнение линии:  Следовательно,
Следовательно, 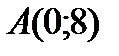 - точка перегиба.
- точка перегиба.
Пример 2. 11. Найти точки перегиба линии  .
.
Решение. 
То есть, вторую производную можно разложить на множители:

Разобьем числовую прямую на интервалы:
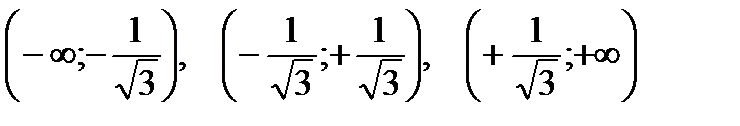 ;
;
Определим знак второй производной в каждом из интервалов. В результате определим участки выпуклости-вогнутости функции.
| x | 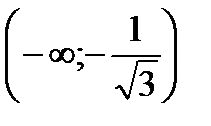
| 
| 
|

| + | - | + |
| y | вогнутая | выпуклая | вогнутая |
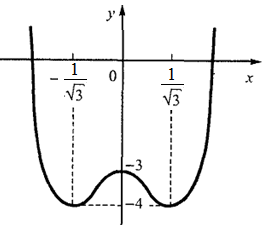 При
При 
 и
и 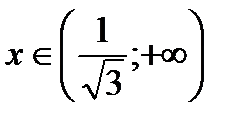 имеем
имеем  - линия вогнута;
- линия вогнута;
при  имеем
имеем 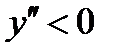 - линия выпукла.
- линия выпукла.
Точки 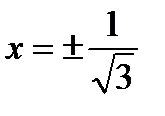 являются точками перегиба (см. рис. )
являются точками перегиба (см. рис. )
Рассмотрим последовательность выполнения операций при исследовании функции и построении ее графика на следующем примере.
Пример 2. 12. Исследуйте функцию и постройте ее график 
Решение.
1) Область определения 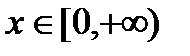
2) Функция не периодическая
3) Функция общего свойства, то есть не относится ни к четным, ни к нечетным.
3) Области возрастания-убывания.
|
|
|
 - функция возрастает;
- функция возрастает;
 - функция убывает.
- функция убывает.
4) Точки экстремумов: 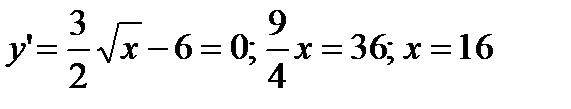

При  имеем минимум. Для определения значения этого минимума подставим
имеем минимум. Для определения значения этого минимума подставим  в уравнение кривой:
в уравнение кривой:  Таким образом, у графика функции имеется точка минимума с координатами (16; -32).
Таким образом, у графика функции имеется точка минимума с координатами (16; -32).
5) Точки пересечения с осями координат.
Для определения ординаты точки пересечения с осью  подставим в уравнение кривой
подставим в уравнение кривой 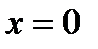 . В результате получим:
. В результате получим: 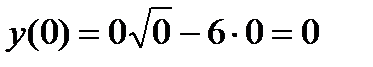 .
.
Таким образом, график функции пересекает ось  при
при 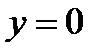 .
.
Для определения абсциссы точки пересечения с осью  подставим в уравнение кривой
подставим в уравнение кривой 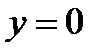 . В результате получим:
. В результате получим:

Таким образом, график функции пересекает ось  в двух точках: при
в двух точках: при  и
и  .
.
6) Области выпуклости-вогнутости.
Для определения участков вогнутости решаем неравенство:  . Оно справедливо для любого
. Оно справедливо для любого 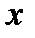 из области определения. Следовательно, график функции всюду вогнут.
из области определения. Следовательно, график функции всюду вогнут.
Для определения участков выпуклости решаем неравенство: 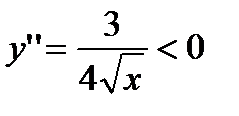 . Оно не имеет решения. Следовательно, график функции не имеет участков выпуклости.
. Оно не имеет решения. Следовательно, график функции не имеет участков выпуклости.
7) Точки перегиба:
Для определения точек перегиба решаем уравнение: 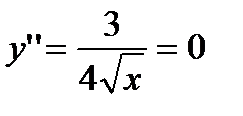 . Оно не имеет решения. Следовательно, график функции не имеет точек перегиба.
. Оно не имеет решения. Следовательно, график функции не имеет точек перегиба.
8) Для построения графика функции начертим оси координат и отметим выявленные нами точки: минимума (16; -32) и пересечения с осями координат (0; 0) и (36; 0), а также области возрастания-убывания функции и ее вогнутости. В р 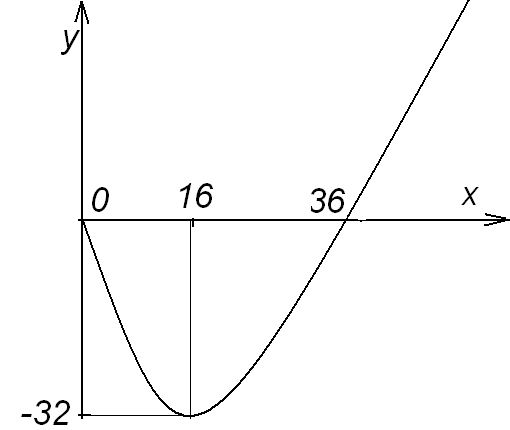 езультате получим график, изображённый на рисунке.
езультате получим график, изображённый на рисунке.
|
|
|


