 |
1.3. Тригонометрическая форма комплексных чисел
|
|
|
|
Решение.
а) Центральной симметрией относительно точки A называют преобразование пространства, переводящее точку X в такую точку X′ , что A — середина отрезка XX′ (см. рис. ).
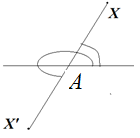Поэтому, в каждой из приведенных точек величина радиус-вектора r останется прежней, а угол 
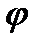изменится на величину 
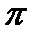. Таким образом, координаты точек, симметричных с указанными точками относительно начала координат, будут: 
б) Для того, чтобы построить на плоскости точку 
, симметричную точке 
относительно прямой l, необходимо от этой точки провести перпендикуляр к прямой и отложить на продолжении этого перпендикуляра точку на расстоянии, равном расстоянию от точки до прямой (см. рис. ).
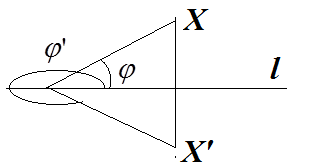Из приеденного рисунка видно, что в точке 
, симметричной точке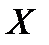 
, радиус-вектор равен радиус - вектору точки , а угол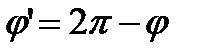 
.
Таким образом, координаты точек, симметричных с указанными точками относительно оси 
, будут: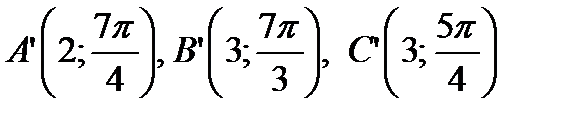 
Пример 1. 7. Определите полярные координаты точек 
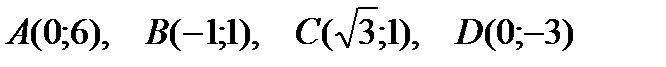
Решение:
Точка A: 
;
Точка B: 
;
Точка C: 
;
Точка D: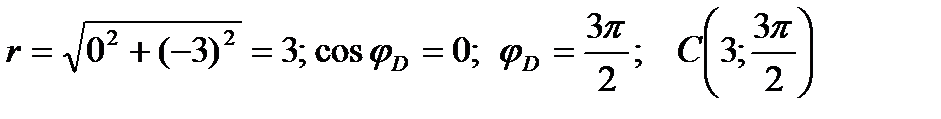 
Аналогично тому, как на числовой прямой откладываются точки с декартовыми координатами, на плоскости можно откладывать точки, соответствующие комплексным числам.
Пусть дано множество комплексных чисел C и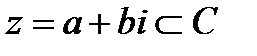 
- произвольное комплексное число.
За единицу на оси Ox примем действительное число 1, а на оси Оу - мнимую единицу 
. Такая плоскость называется комплексной плоскостью.
Пример 1. 7. Данные числа изобразите на комплексной плоскости
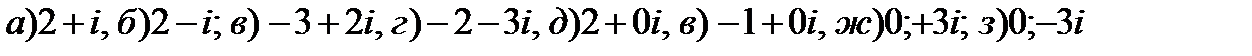Решение
1. 3. Тригонометрическая форма комплексных чисел
Если на плоскости выбрать прямоугольную систему координат Оху, то каждое комплексное число можно изобразить точкой с координатами а и b. Всякое комплексное число z может быть представлено в тригонометрической форме 
.
|
|
|
Число r является модулем, а угол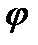 
- аргументом комплексного числа z.
Если 
, то 
. (1. 7).
Модуль комплексного числа z обозначается еще |z|, а аргумент – arg z. Для модулей двух произвольных комплексных чисел справедливы неравенства
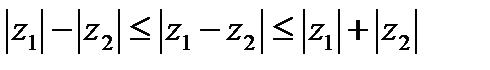
Комплексные числа 
и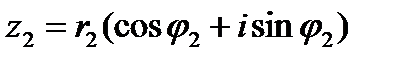 
(заданные в тригонометрической форме) умножаются и делятся соответственно по формулам
Возведение комплексного числа в целую положительную степень осуществляется по формуле:
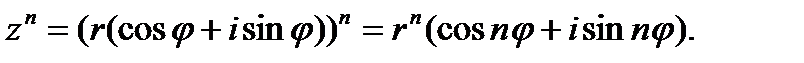(1. 10).
Равенство 
называется формулой Муавра.
Извлечение корня n-й степени из комплексного числа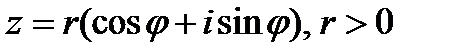 
, дает n различных значений, которые можно найти по формуле
, (1. 11)
где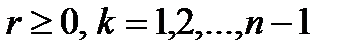 
.
В частности, 
, 
.
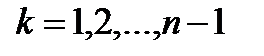На комплексной плоскости эти точки находятся в вершинах правильного многоугольника, с центром в точке (0; 0), одна из вершин этого многоугольника находится в точке (1; 0).
Пример 1. 8. Записать комплексное число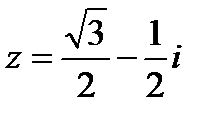 
в тригонометрической форме.
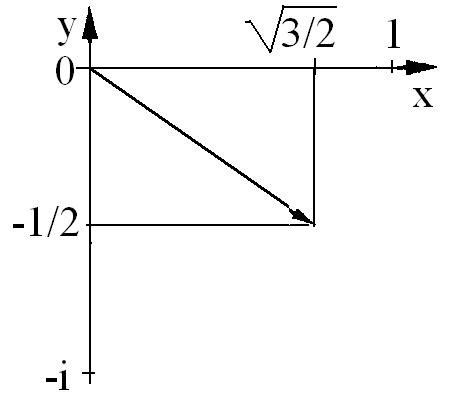Решение. Построим данное число на комплексной плоскости (см. рис. ).
Модуль (радиус-вектор) комплексного числа:
Его аргумент (угол наклона радиус-вектора к оси x)равен:
.
Знак «минус» обусловлен тем, что конец радиус-вектора находится в четвертой четверти комплексной плоскости.
В тригонометрической форме комплексное число записывается в виде:
.
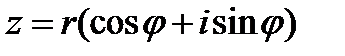Следовательно, заданное число запишется в виде
.
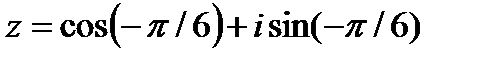Пример 1. 9. Даны два комплексных числа в тригонометрической форме: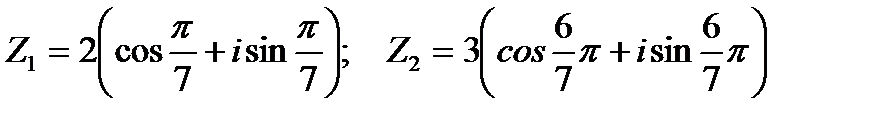 
. Записать их произведение и частное от деления первого числа на второе.
Решение.
Пример 1. 10. Дано комплексное число в алгебраической форме: 
а) перевестиего в тригонометрическую форму;
б) возвести в четвертую степень;
в) извлечь корень третьей степени.
|
|
|
