 |
2.4. Дифференциал функции. Пример 2.13. Рассмотрим геометрический смысл дифференциала функции.. Понятие дифференциала часто применяется при выполнении приближенных вычислений.
|
|
|
|
2. 4. Дифференциал функции.
Пусть функция у=ƒ (х) имеет в точке х отличную от нуля производную 
. Тогда, по теореме о связи функции, ее предела и бесконечно малой функции, можно записать
, (2. 12)
где α → 0 при ∆ х→ 0.
Таким образом, приращение функции ∆ у представляет собой сумму двух слагаемых: 
и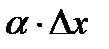 
, являющихся бесконечно малыми при ∆ x→ 0. При этом первое слагаемое есть бесконечно малая функция одного порядка с ∆ х, так как а второе слагаемое есть бесконечно малая функция более высокого порядка, чем ∆ х:
. (2. 13)
Поэтому первое слагаемое 
называют главной частью приращения функции ∆ y. Дифференциалом функции 
в точке х называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается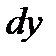 
(или 
):
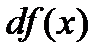(2. 14)
Дифференциал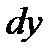 
называют также дифференциалом первого порядка. Найдем дифференциал независимой переменной х, т. е. дифференциал функции 
.
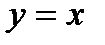Так как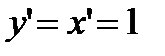 
, то, согласно формуле (2. 1), имеем 
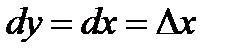, т. е. дифференциал независимой переменной равен приращению этой переменной:
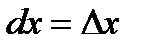. (2. 15)
Поэтому формулу (2. 14) можно записать так:
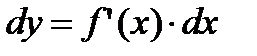, (2. 16)
иными словами, дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной.
Из формулы (2. 16) следует равенство
. (2. 17)
Теперь обозначение производной 
можно рассматривать как отношение дифференциалов 
и 
.
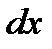Пример 2. 13
Найти дифференциал функции 
.
Решение:
По формуле 
находим 
Пример 2. 14. Найти дифференциал функции 
. Вычислить 
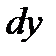при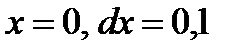 
.
Решение: 
.
Подставив 
и 
, получим 
.
Рассмотрим геометрический смысл дифференциала функции.
|
|
|
Для этого 
проведем к графику функции у=ƒ (х) в точке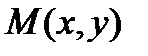 
касательную МТ и рассмотрим ординату этой касательной для точки х+∆ х. На рис. 
. Из прямоуг. 
ка МАВ имеем:
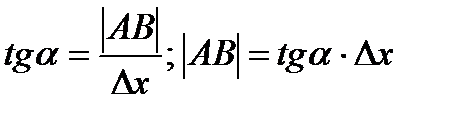. (2. 18)
Сравнивая полученный результат с формулой , получаем 
, т. е. дифференциал функции 
в точке х равен приращению ординаты касательной к графику функции в этой точке, когда х получит приращение ∆ х.
Основные теоремы и формулы дифференцирования легко получить, используя связь дифференциала и производной функции 
.
Понятие дифференциала часто применяется при выполнении приближенных вычислений.
Приращение 
функции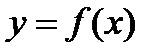 
в точке х можно представить в виде:
, (2. 19)
где 
при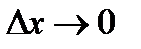 
, или:
. (2. 20)
Отбрасывая бесконечно малую 
более высокого порядка, чем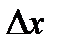 
, получаем приближенное равенство:
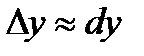, (2. 21)
причем это равенство тем точнее, чем меньше 
.
Это равенство позволяет с большой точностью вычислить приближенно приращение любой дифференцируемой функции.
Дифференциал находится значительно проще, чем приращение функции, поэтому формула 
широко применяется в вычислительной практике.
Пример 2. 15. Найти приближенное значение приращения функции 
при 
и 
.
Решение: Применяем формулу 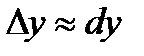, получим:
Итак,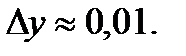 
Посмотрим, какую погрешность допустили, вычислив дифференциал функции вместо ее приращения. Для этого найдем ∆ у:
Абсолютная погрешность приближения равна
Подставляя в равенство 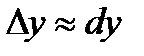значения 
и 
, получим 
или 
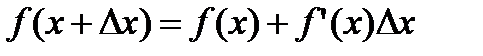. (1)
Формула (1) используется для вычислений приближенных значений функций.
Пример 2. 16. Вычислить приближенно 
Решение: Рассмотрим функцию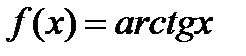 
. По формуле (2. 19) имеем: 
,
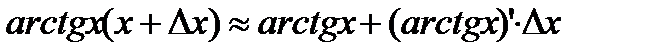т. е. 
.
Так как 
, то при 
и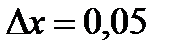 
получаем:
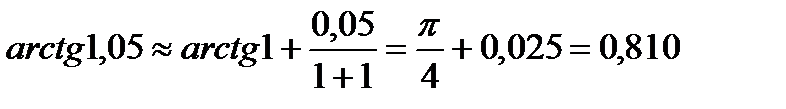
Можно показать, что абсолютная погрешность формулы (1) не превышает величины 
, где М - наибольшее значение 
х)| на сегменте 
.
|
|
|
Пример 2. 17. Какой путь пройдет тело при свободном падении на Луне за 10, 04 с. от начала падения. Уравнение свободного падения тела 
.
Решение: Требуется найти 
. Воспользуемся приближенной формулой 
.
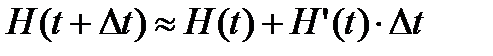. При 
и 
, 
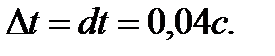, находим
Задача (для самостоятельного решения). Тело массой m=20 кг движется со скоростью ν =10, 02 м/с. Вычислить приближенно кинетическую энергию тела
|
|
|
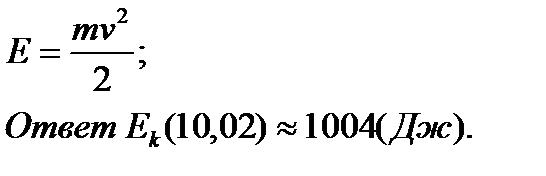
