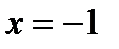 |
1.4. Показательная форма комплексных чисел
|
|
|
|
Решение.
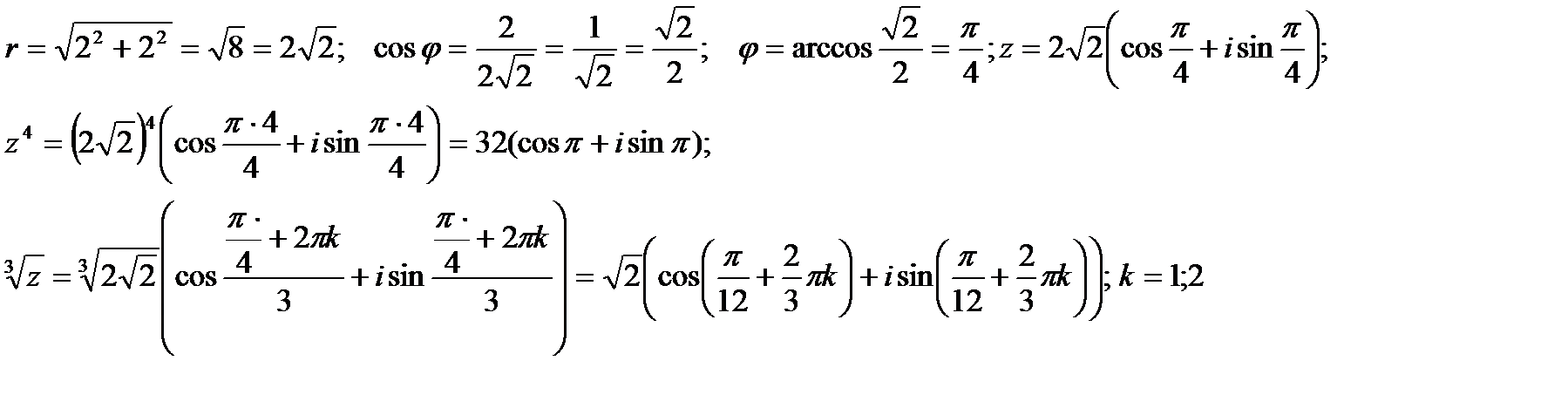
1. 4. Показательная форма комплексных чисел
Комплексное число z может быть представлено и в показательной форме: 
.
В частности: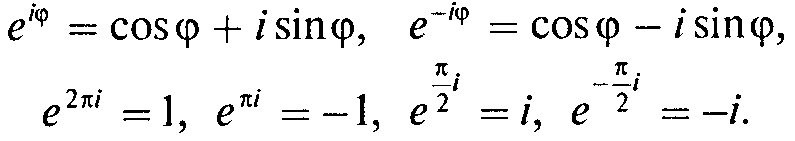 
Для показательной формы комплексных чисел справедливы формулы Эйлера
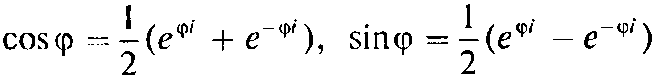
В показательной форме комплексные числа умножаются, делятся и возводятся в степень соответственно по формулам
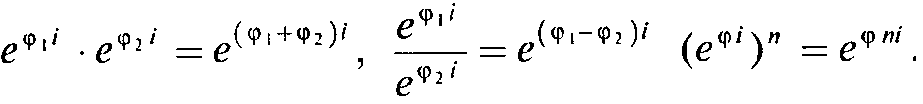
Пример 1. 11. Записать комплексное число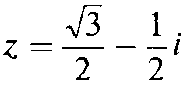 
в показательной форме.
Решение.
Модуль (радиус-вектор) комплексного числа:
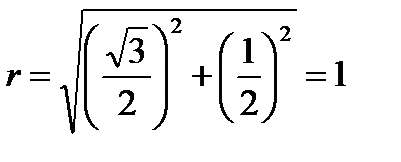
Его аргумент (угол наклона радиус-вектора к оси x)равен:
. Знак «минус» обусловлен тем, что конец радиус-вектора находится в четвертой четверти комплексной плоскости.
В показательной форме комплексное число записывается в виде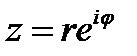 
, поэтому в нашем случае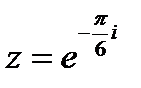 
Пример 1. 12. Даны два комплексных числа в показательной форме: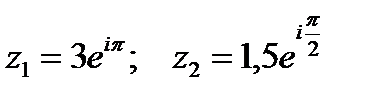 
. Найти а) 
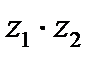; б) 
Решение
а) 
;
б) 
2. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
2. 1. Определение производной и ее свойства
Определим скорость изменения функции 
на проме жутке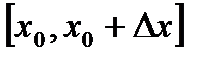 
.
Пусть в точке 
значение функции будет 
. В точке 
оно станет равным 
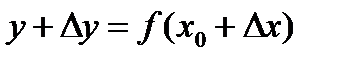. Отношение 
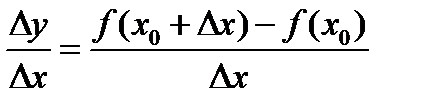будет задавать среднюю скорость изменения функции на промежутке 
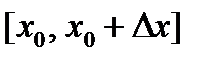, а предел 
, если он существует) - мгновенную скорость изменения функции (или производную функции в точке хо).
Производной функции в точке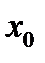 
называется предел отношения приращения 
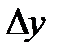функции в точке 
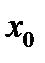к приращению 
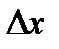аргумента при стремлении приращения аргумента к нулю:
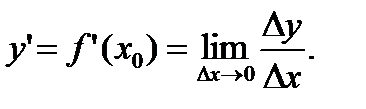(2. 1)
Производная функции 
в точке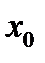 
обозначается одним из символов 
Мы будем пользоваться всеми этими обозначениями по мере необходимости.
Производные элементарных функций
| 
| 
| 
| 
|
| 
| 
| 
| 
|
| 
| 
| 
| 
|
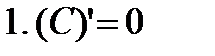
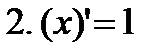
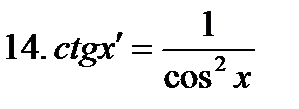
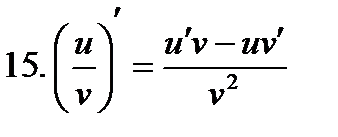
Теорема 1 (производная суммы функций). Если в точке х функци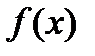и 
и 
имеют производные, то производная от суммы (разности) этих функций в точке х существует и равна сумме (разности) производных этих функций:
|
|
|
(2. 2)
Пример 2. 1. Найти у', если 
.
Решение. 
Теорема 2 (производная произведения функций). Если в точке х функции 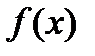и 
имеют производные, то в точке х произведение этих функций имеет производную, которая равна сумме произведений одной из данных функций и производной другой
(2. 3)
Пример 2. 2. Найти у', если 
.
Решение. Обозначив 
и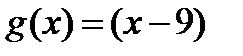 
будем иметь 
Следствие. Постоянный множитель можно выносить за знак производной: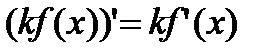 
(2. 4)
Теорема 3 (производная частного двух функций). Если в точке х функции 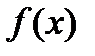и 
имеют производные, причем в точке х функция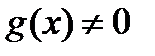 
, то частное этих функций имеет в точке х производную, которая вычисляется по формуле
(2. 5)
Пример 2. 3. Найти у', если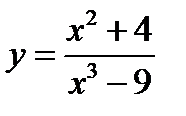 
.
Решение. Обозначив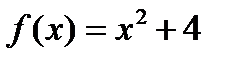 
и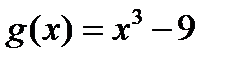 
будем иметь
Теорема 5 (производная сложной функции). Если в точке х функция имеет производную 
, а в точке 
функция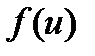 
имеет производную 
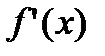, то производная от сложной функции 
в точке х существует и определяется по формуле:
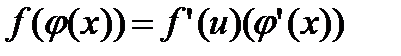, (2. 6)
где 
.
Пример 2. 4. Найти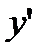 
, если 
Решение. Функция 
- сложная. Во-первых, она – степенная, во вторых – тригонометрическая. Поэтому 
Пример 2. 5. Найти 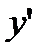, если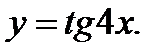 
Решение. 
Пример 2. 6. Найти 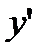, если 
Решение. 
2. 2. Возрастание и убывание функции, ее экстремумы
Рассмотрим функцию 
, непрерывную вместе со своей производной на некотором промежутке. Геометрический смысл производной заключается в том, что 
, где 
-угол наклона касательной к положительному направлению оси Oх.
 
|
). Касательные, проведенные к кривой в любой точке этого промежутка, образуют с осью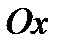 
тупой угол, тангенс которого отрицателен, т. е. для 
величина 
. Значит, если функция убывает на некотором промежутке, то ее производная на этом промежутке отрицательна. |
|
|
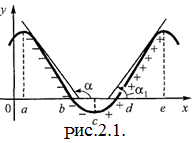
Если с возрастанием значения аргумента х значение функции yвозрастает, то функция является возрастающей (на рис. в интервале 
). Касательные, проведенные к кривой у = f(х) в любой точке этого промежутка, образуют с осью Ох острый угол, тангенс которого положителен, т. е. для 
величина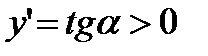 
. Значит, если функция возрастает на некотором промежутке, то ее производная на этом промежутке положительна.
Теорема. Если функция f(x) имеет положительную производную в каждой точке интервала l, то эта функция возрастает на этом интервале. Если функция f(x) имеет отрицательную производную в каждой точке интервала l, то эта функция убывает на этом интервале.
Замечание. Интервалы, в которых функция возрастает или убывает, называются интервалами монотонного изменения функции.
Мы предположили, что наша функция и ее производная непрерывны, а значит они меняют знаки с «-» на «+» или с «+» на «-» только при переходе через нуль, т. е. в тех точках, в которых интервал убывания сменяется интервалом возрастания, (в которых у' = 0). В этих точках мгновенная скорость изменения функции равна нулю. Точки области определения функции, в которых производная функции равна нулю, бесконечности или не существует, называются критическими. На рис. 2. 1. имеются три критические точки а, с, е.
Пример. 2. 7. Найти интервалы монотонного изменения функции
Решение. Найдем производную: 
.
Эта функция непрерывна. Чтобы найти критические точки, приравняем производную нулю и найдем корни полученного уравнения:
Разобьем числовую прямую на интервалы: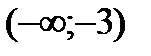 
; 
; 
.
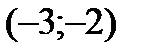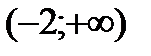Определим знак производной в каждом из интервалов. В результате определим участки возрастания-убывания функции.
| x |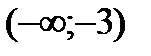
|
|
|
| + | - | + |
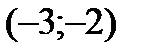
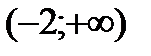
| y | возрастает | убывает | возрастает |
Таким образом, пр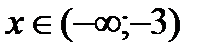и 
и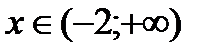 
функция возрастает, при 
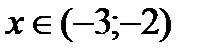- убывает.
Наименьшее значение функции в окрестности некоторой точки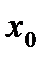 
называют минимальным значением (min), а наибольшее ее значение - максимальным (max). Дадим строгое определение этим понятиям.
|
|
|
Точка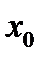 
из области определения функции f называется точкой минимума этой функции, если у этой точки есть окрестность 
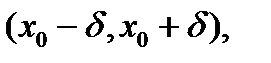во всех точках которой, не совпадающих с точкой ,
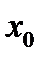(2. 7)
Точка 
из области определения функции f называется точкой максимума этой функции, если у этой точки есть окрестность 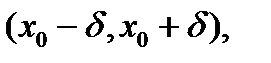во всех точках которой, не совпадающих с точкой ,
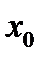(2. 8)
Максимумы и минимумы называются экстремумами функции.
Замечание. Так как речь идет об экстремальных значениях функции в окрестностях некоторых точек, то иногда определенные нами экстремумы называются локальными экстремумами.
У непрерывной функции точки минимума и максимума обязательно чередуются.
Рассмотрим необходимое условие существования экстремума.
Теорема Ферма. Если внутренняя точка xо из области определения непрерывной функции f(х) является точкой экстремума и в этой точке существует производная, то она равна нулю, т. е.
(2. 9)
Пример. 2. 8. Исследовать на экстремум функцию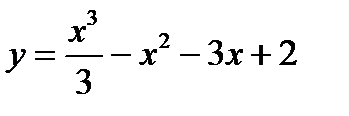 
.
Решение. Функция 
точек разрыва не имеет. Область определения – вся числовая ось. Исследуем данную функцию на экстремум. Определим критические точки. Для этого находим первую производную данной функции и приравниваем ее к нулю: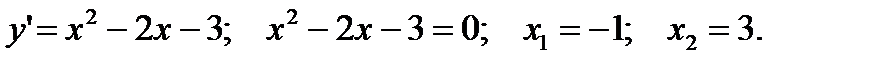 
Разобьем числовую прямую на интервалы: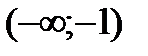 
; 
; 
.
Определим знак производной в каждом из интервалов. В результате определим участки возрастания-убывания функции.
| x |
|
|
| |||
|
| + | - | + | |||
| y | max при | min при | ||||
При 
производная меняет знак с «плюса» на «минус», то есть в этой точке функция имеет максимум. Для определения значения этого минимума подставим в первоначальное выражение функции , в результате получим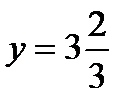 
.
При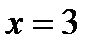 
производная меняет знак с «минуса» на «плюс», то есть в этой точке функция имеет минимум. Для определения значения этого максимума подставим в первоначальное выражение функции 
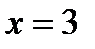, в результате получим 
.
|
|
|
Таким образом, функция 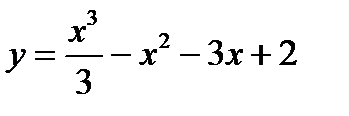имеет две точки экстремума:
- максимум;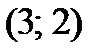 
- минимум.
|
|
|
