 |
3.4. Площади плоских фигур и объемы тел вращения
|
|
|
|
Решение
Так как плотность распределена неравномерно, то для наиболее точного ее нахождения разобьем весь стержень точками на 
достаточно малых частей (см. рис. )
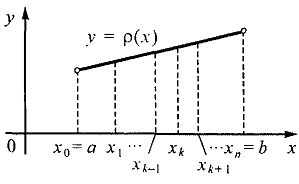Обозначим длину отрезка 
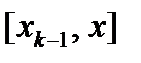через 
. В силу того, что длины отрезков малы, в границах каждого из них плотность стержня можно считать постоянной и равной 
, где 
- одна из точек k-го отрезка 
. Тогда масса этого отрезка стержня равна 
. Масса всего стержня приближенно равна:
.
При стремлении 
к нулю, эта сумма становится равной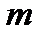 
, то есть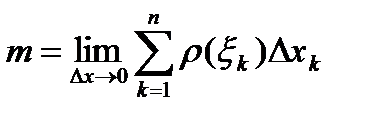 
Задача о площади криволинейной трапеции. Дана плоская фигура, ограниченная графиком функции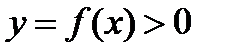 
и отрезками прямых 
. Функция 
определена, непрерывна и неотрицательна в промежутке [а, b]. Вычислить площадь S полученной фигуры (аАВb), называемой криволинейной трапецией.
Решение. Для того чтобы вычислить искомую площадь, разобьем промежуток [а, b] на nпроизвольных частей: 
, длины которых обозначим соответственно 
. Через каждую точку деления проведем прямую, параллельную оси ординат. Эти прямые разделят данную фигуру на nполос. Заменим каждую из этих полос прямоугольником, основание которого то же, что у полосы, а высота совпадает с одной из ординат точек графика функции в этой полосе.
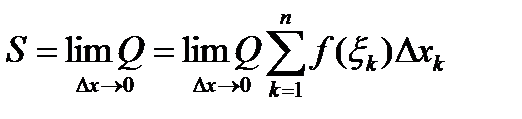
Обобщим рассуждения, проведенные при решении двух предыдущих задач о массе прямолинейного стержня и о площади криволинейной трапеции. Пусть некоторая функция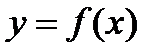 
задана на промежутке [а, b] и непрерывна. При разбиении промежутка [а, b] на n частей, таким образом, что максимальная длина отрезков разбиения стремится к нулю 
при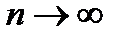 
) обе задачи свелись к составлению суммы 
, где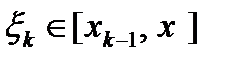 
, число слагаемых которой неограниченно растет, а каждое слагаемое стремится к нулю. Эта сумма называется интегральной суммой.
|
|
|
Определение. Предел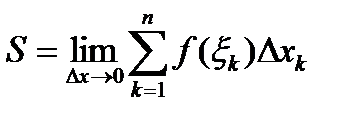 
называют определенным интегралом от функции 
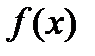на промежутке [а, b] и обозначают 
т. е.
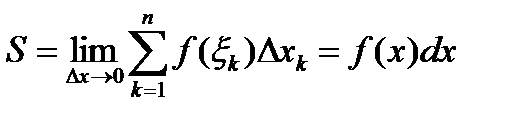(3. 7)
Число 
называется нижним пределом интеграла, b - верхним.
Промежуток [а, b] называется промежутком интегрирования, х - переменной интегрирования.
Теорема. Определенный интеграл функции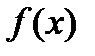 
, непрерывной на промежутке [а, b], равен разности значений любой ее первообразной в точках b и а
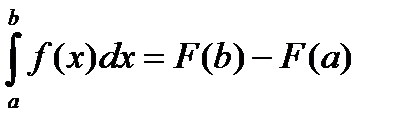(3. 8)
: Правая часть формулы часто записывается как 
Формула (3. 8) получила название формулы Ньютона-Лейбница.
Чтобы вычислить определенный интеграл, достаточно найти неопределенный интеграл и в полученное выражение подставить вместо переменной x; сначала верхний предел b, а затем нижний а и из первого результата вычесть второй.
Пример 3. 10. Вычислить 
Решение. Находим неопределенный интеграл: 
Найдя значение 
сначала при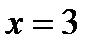 
, а затем при 
, вычислим разность:
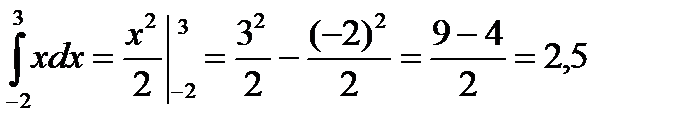
Пример 3. 11. Вычислить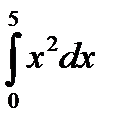 
Решение.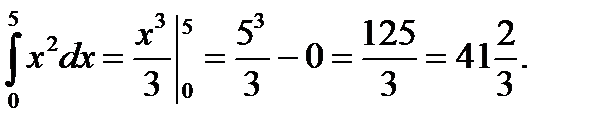 
При формулировке свойств определенных интегралов использовали источник [5] и исходили из предположения, что функции заданы и дифференцируемы на промежутке [a, b]
1) 
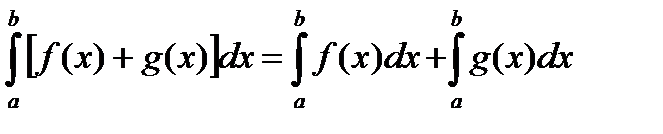, (3. 9)
т. е. интеграл суммы равен сумме интегралов слагаемых.
2) 
, (3. 10)
где 
– константа; т. е. постоянный множитель можно выносить за знак интеграл.
3) Пусть f(x) непрерывна на промежутке [a, b]. Если этот промежуток точкой c разложен на части [a, c] и [c, b], то интеграл по всему промежутку оказывается равным сумме интегралов по его частям, т. е.
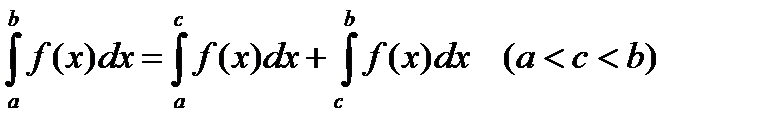(3. 11),
4) Если f(x) - любая функция, то: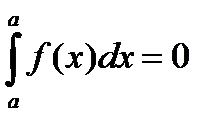 
, (3. 12)
т. е. интеграл с совпадающими нижним и верхним пределами равен нулю.
5) 
, (3. 13)
то есть перемена мест пределов интегрирования приводит к изменению знака интеграла на противоположный.
|
|
|
6) Если f(x) - непрерывная функция, заданная на промежутке [a, b], то существует такая точка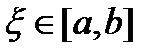 
, что 
(3. 14)
7) Если f(x) - неотрицательная непрерывная функция и нижний предел интеграла не больше верхнего, то и сам интеграл будет числом неотрицательным
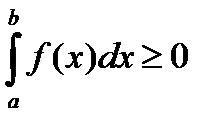. (3. 15)
9) Если a ≤ b, а f(x) и u·g(x) - две непрерывные функции, которые на [a, b] удовлетворяют условию f(x) ≤ g(x), то
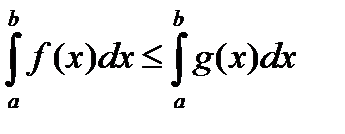(3. 16)
3. 4. Площади плоских фигур и объемы тел вращения
Если непрерывная линия задана уравнением 
то площадь криволинейной трапеции, ограниченной этой линией, двумя прямым 
отрезком оси абсцисс а < х < b, вычисляется по формуле
(3. 17)
Пример 3. 12. Вычислить площадь, ограниченную графиками функций: 
Решение. Построим графики данных функций, найдя предварительно точки их пересечения путем решения системы: 
. Решив эту систему, получим точки O(0; 0) и A(1; 1).
|
предполагает вычисление площади, ограниченной графиком функции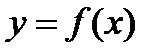 
, осью х и прямыми . В данной задаче, взяв 
, мы вычислим площадь треугольника ОАВ, а взяв 
, вычислим площадь криволинейного треугольника 
Затем из первого результата вычтем второй. Итак,
и 
Следовательно, площадь S фигуры, ограниченная заданными линиями
кв. ед.
Пример 3. 13. Вычислить площадь, ограниченную линией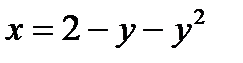 
и осью ординат.
Решение. В этом примере искомая площадь ограничена линией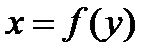 
и может 
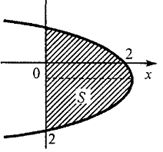быть вычислена с помощью интеграла 
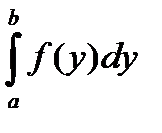, где а и b -ординаты точек пересечения данной кривой с осью ординат. Найдем эти ординаты из системы:
Следовательно, 
(кв. ед. ).
Пример 3. 14. На схеме, в системе координат Оху, излучина реки образует кривую 
. По оси 
проходит шоссе. Найдите координаты пересечения реки и шоссе и вычислите, какую площадь занимает пашня между рекой и линией шоссе.
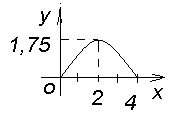Решение. Определим координаты точек пересечения кривой и оси 
из системы уравнений: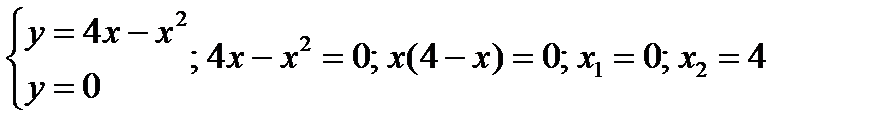 
(см. рис. ).
Пример 3. 15. Вычислите площадь фигуры, ограниченной линиями: 
Решение. 
Если криволинейная трапеция, ограниченная линией 
и прямыми 
, вращается вокруг оси х, то объем тела вращения вычисляется по формуле: 
(3. 18)
Если фигура, ограниченная линиями 
и 
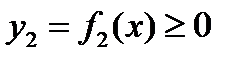
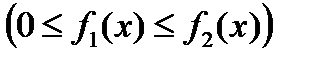прямыми 
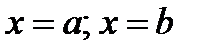, вращается вокруг оси Oх, то объем тела вращения вычисляется по формуле: 
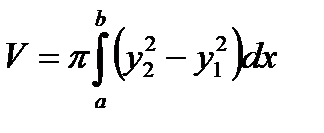(3. 19)
|
|
|
Пример 3. 16 Найдите объем шара, полученного при вращении полукруга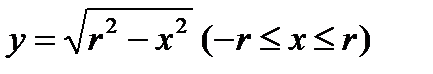 
вокруг оси Ох.
Решение. По формуле (3. 18) имеем:
Пример 3. 17. Найдите объем тел, образованных вращением вокруг оси Ох фигур, ограниченных линиями: 
Решение. Определим координаты точки пересечения этих линий из системы: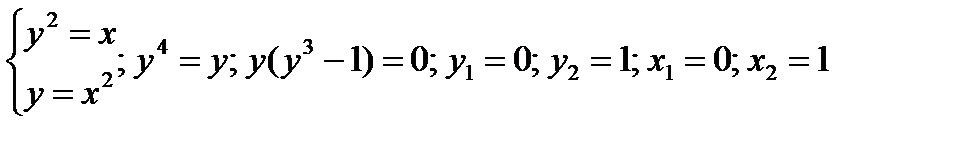 
Таким образом, имеем две точки пересечения линий: 
. По формуле (3. 19) имеем:
|
|
|
