 |
Решение. 3. Интегральное исчисление. 3. 1. Первообразная. Неопределенный интеграл и его свойства. Пример 3. 1. Найти первообразную для функции.
|
|
|
|
Решение.
Находим скорость
Находим ускорение
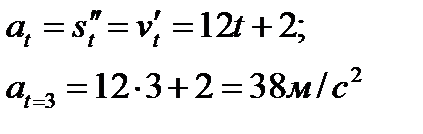
3. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
3. 1. Первообразная. Неопределенный интеграл и его свойства
Функция F называется первообразной для функции f на некотором промежутке, если для всех х из этого промежутка существует производная F'(х) , равная 
, т. е. 
. (3. 1)
Пример 3. 1. Найти первообразную для функции.
Решение. Функция 
есть первообразная для функции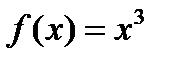 
на промежутке 
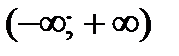, так как 
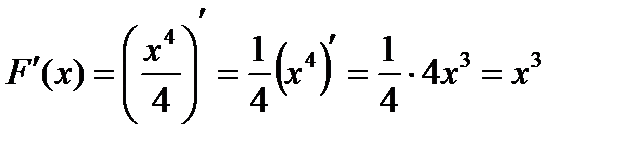для всех 
.
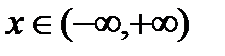Но функции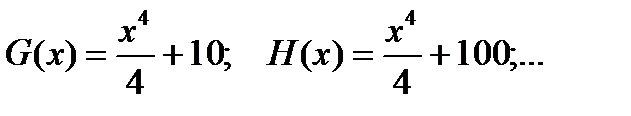 
также имеют производную, равную 
поэтому и все эти функции являются первообразными для функции 
на множестве R.
К выражению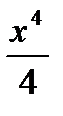 
можно прибавить любую постоянную С. Поэтому решение задачи нахождения первообразной не единственно и, если решения существуют, то их бесконечно много.
Множество первообразных для данной функции 
называется неопределенным интегралом и обозначается 
, (3. 2).
где - подынтегральная функция; 
- подынтегральное выражение; 
- переменная интегрирования; С - константа.
Пример 3. 2. Найти неопределенный интеграл 
.
Решение 
Интегрирование есть действие, обратное дифференцированию.
Неопределенные интегралы элементарных функций
|  
| 
|
| 
| 
|
| 
| 
|
| 
| 
|
|
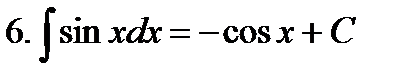
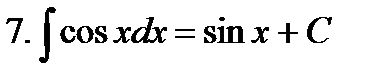
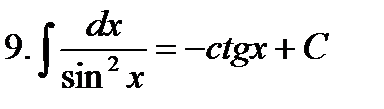
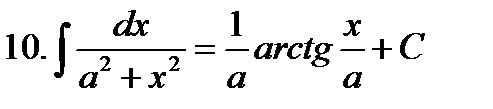
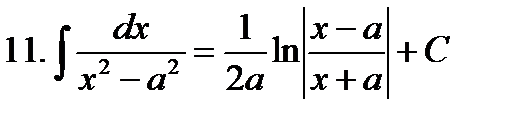
Свойства неопределенных интегралов:
1. Постоянный множитель можно вынести за знак интеграла:
(3. 3)
2. Интеграл алгебраической суммы равен алгебраической сумме интегралов:
(3. 4)
3. Вид интеграла не зависит от вида переменной интегрирования:
|
|
|
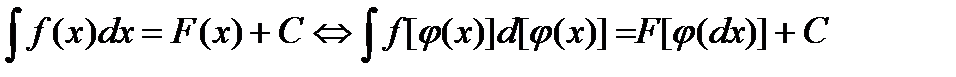. (3. 5)
или, что тоже самое,
,
где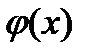 
- функция, непрерывная вместе со своей производной.
4. Имеет место следующее равенство:
(3. 6)
3. 2. Методы интегрирования
I. Непосредственное интегрирование.
Этот способ интегрирования предполагает такое преобразование подынтегральной функции, которое позволило бы использовать для решения табличные интегралы.
Пример 3. 3. Найти 
Решение. Воспользуемся свойством 2. интеграла: интеграл от суммы (разности) функций равен сумме (разности) интегралов от этих же функций.
Пример 3. 4. Найти 
Решение. Приведем интеграл к табличному виду. Для этого раскроем скобки в числителе и разделим почленно числитель на знаменатель.
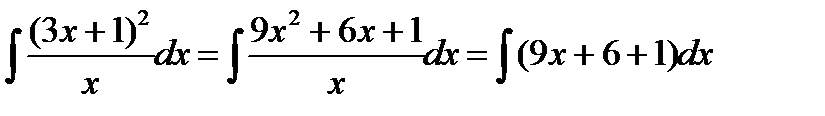
Затем воспользуемся указанным выше свойством интеграла суммы (разности) функций: 
II. Метод подстановки.
Этот метод называют также методом замены переменной. Использование этого метода основано на свойстве 3 интеграла.
Пример 3. 5. Найти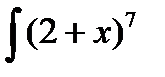 
Решение. Введем новую переменную: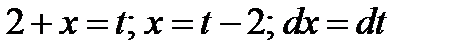 
.
Найдем интеграл: 
Выразим результат через первоначальный аргумент: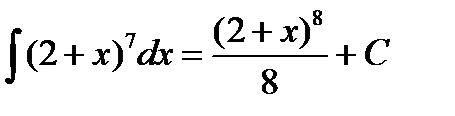 
Пример 3. 6. Найти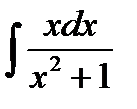 
Решение. Сделаем подстановку 
Надо определить, чему равен dx. Для этого продифференцируем выражение 
, в результате чего получим 
.
Подставим все это в первоначальный интеграл, в результате чего будем иметь:
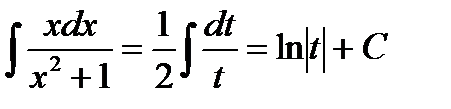
Выразим результат через первоначальный аргумент: 
Этот пример дает возможность сделать следующий общий вывод: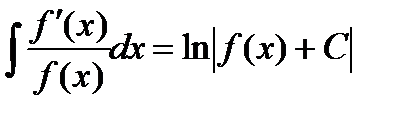 
.
III. Метод интегрирования по частям.
Использование этого метода основано на свойстве (4) интеграла: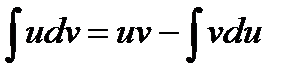 
Пример 3. 7. Найти 
.
Решение. Обозначим 
.
Подставим полученные данные в первоначальное выражение:
Пример 3. 8. Найти 
.
Решение. Интегрируем по частям
Тогда 
Пример 3. 9. Найти 
Решение. Интегрируем по частям
|
|
|
Тогда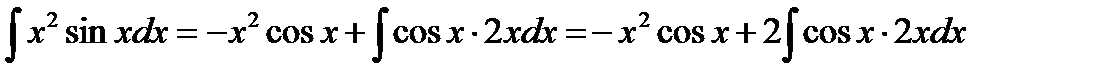 
.
Подставим значение интеграла из примера 3. 8, получим
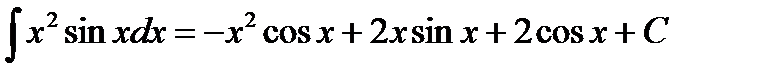
3. 3 Определенный интеграл и его свойства
Многие задачи естествознания и техники получили решение благодаря одному из основных понятий математического анализа - определенному интегралу. Нахождение площадей, ограниченных кривыми, длин дуг, объемов, работы, пути, скорости, моментов инерции и т. д., сводится к его вычислению. Рассмотрим задачи, приводящие к понятию определенного интеграла.
Задача о массе прямолинейного стержня. Дан тонкий стержень длины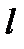 
, его масса распределена неравномерно с плотностью 
. Найти массу всего стержня.
Решение. Разберем условие задачи. Под тонким стержнем мы будем понимать отрезок прямой, ограниченный точкам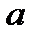и 
и 
числовой оси 
. Плотность вещества стержня в данной точке есть предел средней плотности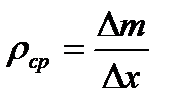 
, где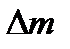 
- масса отрезка 
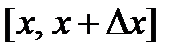, при стремлении 
к нулю.
Требуется найти массу стержня.
|
|
|
