 |
Слушатель: 1/2 + 1/4. Слушатель: Ноль. Другой слушатель: Единицу. Слушатель: Да.
|
|
|
|
Слушатель: 1/2 + 1/4.
А. С.: А если я проделаю это бесконечное количество раз? Тогда что я получу?
– + – + – Н h =1
4 816
Слушатель: Ноль.
Другой слушатель: Единицу.
А. С.: Я получу число один, причем в точности число 1.
Почему в точности? Потому что каждый раз число получалось
не больше единицы, это очевидно. Значит, мы не можем получить
число больше единицы. Но какое бы маленькое число мы не взяли, 1
в конце концов – станет меньше его. На самом деле у нас в знаменателе вместо п стоят степени двойки: 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, 8192...
Они очень быстро растут, поэтому – – очень быстро уменьшается. И в итоге очередное расстояние до числа «1» станет меньше любого наперед заданного числа. То есть они уходят в ноль. Получается, что наша сумма неограниченно приближается к единице, и вот тогда математик говорит: «Следовательно, она равна единице». Всё. Вот он, предельный переход. Это то, что учат в матанализе на любом факультете любого вуза. Больше ничего в нём нет11.
Слушатель: А если здесь просто включить житейскую мудрость и подумать, что мы отрезали от одного целого яблока?
А. С.: Да. В данном случае можно. Но житейская мудрость – она такая штука, что она иногда не работает. Давайте решим такую задачу.
Кузнечик сначала прыгает на один метр, а потом на ^ метра,
111 а потом – на тг, а потом – на т, а потом – на „. и так далее...
о 4 о
Вот он прыгает и прыгает. Есть ли предел того, куда он может
допрыгать?

Слушатель: Да.
А. С.: При наивном подходе кажется, что есть, потому что «шажки все меньше и меньше». Но тем не менее, друзья мои, вы будете смеяться, или удивляться, или поражаться, или возмущаться, но
|
|
|
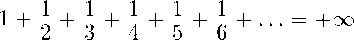
(т. е. эта сумма равна бесконечности).
Нет никакого предела тому, куда может дойти этот кузнечик. Никакого. Он может дойти до Луны, может дойти до Солнца, и далее, прямо в Космос!
В прошлом примере у нас шажки были всё меньше и меньше, они стремились к нулю, но в сумме получилось число, равное единице. А эти шажки, хотя и тоже всё меньше и меньше, но уйти этими шажками можно до бесконечности, вот такая загадка природы. Хотите, покажу, почему?
Слушатели: Да.
А. С.: Вот смотрите, сейчас я с кузнечиком сделаю страшную штуку, я сейчас его заменю на кузнечика, который шагает еще медленнее. А именно: кузнечик этот будет шагать следующим образом.
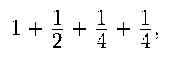
то есть вместо одной трети, он шагает на одну четверть. Не правда ли, такой кузнечик будет отставать от первого?
Слушатель: Да.
А. С.: А теперь вместо одной пятой я сразу одну восьмую поставлю. То есть первый кузнечик на одну пятую шагает, а мой, второй – он сразу прямо раз – и «скис» – только на одну восьмую. И так 4 раза по одной восьмой:
1+1+1 1 1+1+1+1
4 4 8 8 8 8
А вместо одной девятой я напишу что?
Слушатели: Одну шестнадцатую?
А. С.: Правильно. Одну шестнадцатую, и так повторим эту добавку 8 раз. А дальше я что напишу? Вместо одной семнадцатой? Слушатель: Одна тридцать вторая.
А. С.: Одну тридцать вторую. Отлично. И повторим ее 16 раз!
1+1+I+I+I+1+I+1+
4 4 8 8 8 8
‑ I–=–I–=–I–=–I–=–I–=–I–=–I–=–I–=–I–=–I‑
16 16 16 16 16 16 16 32
Похоже, что второй кузнечик всё время отстает от первого. Небось, он совсем отстанет от него: ведь первый, как мы утверждаем, ускачет на бесконечное расстояние. Нет, самое страшное здесь вот
что. Хоть второй и отстает, но он ТОЖЕ ускачет на бесконечное
1 1
расстояние. Чему равна сумма ‑ j‑ + ‑ j‑ (двух равных слагаемых)?
Слушатель:
А. С.: Отлично. А такая:
1+1 + 1 + 1?
8 8 8 8
Слушатель: Одна вторая.
А. С.: Тоже одна вторая! А для шестнадцатых долей? Слушатель: Тоже одна вторая.
|
|
|
А. С.: Теперь вы поняли, почему он дойдет до бесконечности? Слушатель: Нет.
А. С.: Потому что мы каждый раз, в каждой очередной группе шагов, будем получать в сумме Значит, он всё снова и снова отходит на 0, 5. А таких «одних вторых »‑ то бесконечное количество штук. Вот он и уйдет на бесконечность.
1 + 1 = 1 4 4 2’
|
|
|


