Слушатели: Да.

А. С.: Теорема Пифагора говорит, что квадрат гипотенузы ра­вен сумме квадратов катетов16. Давайте я покажу доказательство этого без единой формулы. Теорему Пифагора не нужно доказы­вать формулами, ее нужно просто узреть, увидеть, она видна. Вот смотрите, я беру вот такое равенство: а ²  + Ь² = с².

 

щади и из площади второго квадрата те же 4 площади. Значит, площади оставшегося должны быть одинаковыми. В одном случае остается с², а в другом – сумма а ²  + Ь². Значит,

 

2, 1, 2 2 а + о = с.

Теорема Пифагора доказана. Но это было небольшое отступление. Я хотел сказать, что диагональ квадрата со стороной 1 по теореме Пифагора равна корню из двух, согласно тому, что я нарисовал, она и в самом деле ему равна. Древние ничего не могли с этим числом поделать. Потому что, если отложить отрезок, равный на­шей диагонали, от нуля, то вы попадете в точку, которая заведомо не равна никакому числу вида Щ. Ни при каких тип. Вы пере­берете все целые числа, и в числителе, и в знаменателе, и никогда не получите число, которое в точности совпадет с корнем из двух.

Есть очень много разных доказательств этого факта, и одно из них совершенно геометрическое. Мы разберем ниже два разных доказательства.

Мы сейчас придумаем некую процедуру, которую мы приме­ним к любому рациональному числу, и она всегда будет конечной. А дальше, я вам покажу, что та же самая процедура для числа «корень из двух» никогда не прекращается, тем самым это чи­сло не может быть рациональным

Слушатель: То есть это несуществующее число?

А. С.: Существующее, но не в этом круге подозреваемых лиц. Это число существует, и оно очень нервировало греков, они не хо­тели допустить, что оно существует. Однако они отлично знали, что оно нужно для вычислений, но не выражается в виде отноше­ния целых чисел. Они не понимали, что с ним делать. Вроде чи­сло не существует, а оно‑ таки есть. Оно не должно существовать, но оно существует. Числа, которые не представляются в виде Щ, называются иррациональными.

Что такое вообще «иррациональность»? Нелогичность. Нера­зумность. Иррациональное поведение, например. Но в математике, в отличие от философии, есть совершенно конкретные объекты, иррациональные числа. Это такие числа которые не представля­ются в виде Щ‑. Тем не менее, они вполне себе логичные и очень даже разумные.

Слушатель: А числа тип, они целые?

А. С.: Целые. Непременно целые числа. Иррациональные чи­сла – это числа, которые не являются отношением двух целых чисел. Рациональное число – это отношение двух целых.

Есть еще одно труднопроизносимое слово, оно тоже в философ­ском смысле кое‑ что означает. Слово «трансцендентно». Что же оно означает в житейском (не математическом) смысле?

Слушатель: Находится за пределами.

А. С.: За пределами чего бы то ни было.

Слушатель: То есть иррациональное поведение – это поведе­ние странное, но всё же в каких‑ то рамках. А трансцендентное – это что‑ то за пределами понимания окружающих.

А. С.: В математике трансцендентные числа – это тоже опре­деленный термин. Им противопоставляются алгебраические числа. Согласно строгому математическому определению, алгебраическое число – это корень многочлена с целыми коэффициентами. Транс­цендентным числом называется такое число, что ни один много­член с целыми коэффициентами не обнуляется при подстановке вместо переменной х этого числа.

Внутри множества алгебраических чисел живут как все раци­ональные, так и корни любой степени и много, много чего еще. Очень много разных чисел. И вот трансцендентные – это те чи­сла, которые не являются алгебраическими. Выдумать неалгебра­ическое число достаточно трудно. Сначала думали, что все чи­сла алгебраические. А в XIX веке произошел взрыв в математи­ке, было обнаружено огромное количество неалгебраических чи­сел – но это было только в XIX веке. Примером трансцендент­ного числа является знаменитое число «пи» – длина окружно­сти с диаметром, равным 1. Доказательство трансцендентности одного‑ единственного числа «пи» занимает 10 лекций на 4‑ м кур­се мехмата МГУ. Очень мало людей на Земле, которые знают это

целой части дробная часть не окажется равна нулю. Если этого никогда не случится, то исходное число окажется разложенным в бесконечную цепную дробь.

 

Итак, продолжим разложение числа – в цепную дробь:

 

Стоп, машина. После выделения целой части из числа 2 дробная

 

часть равна нулю. Значит, числу ^ «суждено» разлагаться в ко­нечную цепную дробь. Если кто не верит, можете упростить эту «6­этажную» дробь, сделав из нее обыкновенную. Конечно, она будет 21

равна 7^7.

Эту операцию придумал Евклид. Называется она – разложе­ние числа в «цепную дробь». Обратите внимание. На последнем

шаге мы попали в целое число 2 при переворачивании дроби На этом всё заканчивается, так как из целого числа не удастся выудить дробную часть.

Другой пример:

1? ^{= 1 +} Ж ^{= 1 +} ^ ^{= 1 +} 77Т‑ ‑

„ 3 1 + 1

 

Опять пришли к целому числу. Ура. Закончили.

Евклид утверждал, что для любой дроби за конечное число ша­гов мы придем к целому числу. Попробую это пояснить «без фор­т, . . 17284 мул». Вы берете какую‑ то очень большую дробь, например, ·

Что происходит в процессе, предложенном Евклидом? Мы про­сто несколько раз делим с остатком, и всё. На каждом шагу мы получаем «нечто» плюс что‑ то меньшее, чем то, на что мы делим. Идея в том, что на каждом шагу числа будут уменьшаться. Числи­тель и знаменатель целые положительные числа, и они будут уменьшаться. Но целое число, любое положительное целое число, не может бесконечно долго уменьшаться, оно в конце концов «за­кончится». Оно придет к нулю за конечное число шагов.

То есть любое рациональное число непременно порождает ко­нечную цепную дробь. А теперь я возьму и покажу, что корень из двух порождает бесконечную цепную дробь.

Вот этот фокус‑ покус. Если «корень из двух» рациональ­ное число, то процедура, которую я только что проводил, должна закончиться. Берем корень из двух. Между какими целыми чи­слами он расположен? Вспомним, что, согласно теореме Пифагора, корень из двух это длина диагонали квадрата с единичной сто­роной. Поэтому он расположен между 1 и 2 (см. рис. 65).

 

Значит, корень из двух = 1 + дробная часть (она примерно равна 1, 4142 ‑ 1 = 0, 4142).

Что я сделал? Прибавил единицу и отнял единицу. Больше ни­чего не делал. То есть я выделил целую часть из «корня из двух» (дробная же часть записана в скобках; она равна примерно 0, 414).

 

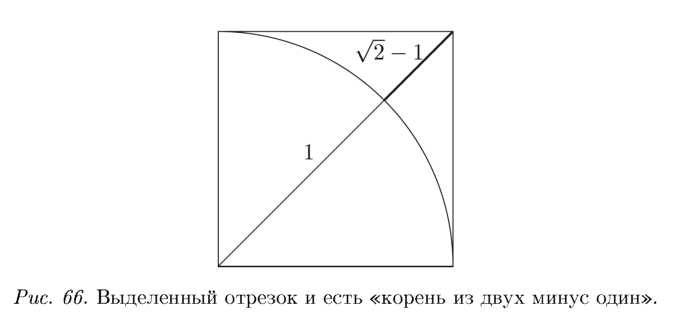
Для получения дробной части я взял окружность радиуса 1, провел ее до пересечения с диагональю, и всё (см. рис. 66). Эта часть, без сомнения, меньше единицы. Далее для краткости обо­значим «корень из двух» через К. А выражение К – 1 обозначим за С. Значит, С 1. Поэтому будем эту часть «переворачивать»:

С =   А‑ =   ¹ 1 К + 1'

С

Поясню, почему – превратилось в К + 1.

О

Я возьму числитель и знаменатель и домножу на одно и то же число (это не изменит значения дроби). Я числитель и знаменатель умножу вот на такое число: К + 1. Помним, что К · К = 2. Начинаем открывать скобки:

1 (к +1)· 1 _ к + 1 _k + i__fm С “ (К + 1)‑ (К‑ 1) K‑ K^l“2^1^{_K + i}‑

А теперь, по общему правилу, выделяем целую часть.

Между каким двумя целыми числами находится \/2 + 1? Слушатель: Между двойкой и тройкой.

А. С.: Конечно. Поэтому, если я по правилу Евклида выделяю из него целую часть, то она равна?

 

⇐ Предыдущая13141516171819202122Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: