Слушатель: 2.

Не правда ли, мы уже сталкивались выше с такой дробной частью? Слушатель: И так до бесконечности будет повторяться?

А. С.: И так до бесконечности. Значит, исходное число – не ра­циональное.

Мы получим бесконечную цепную дробь:

 

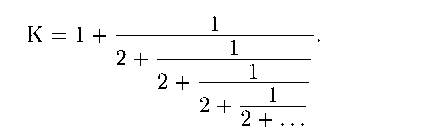
Только бесконечное число шагов приведет вас к числу, равно­му К*. Но не конечное – а значит, число К иррационально, что и требовалось доказать. Теперь вы знаете, что есть такие числа, страшные числа, которые не представляются в виде «количество яблок поделить на количество гостей».

Мы еще вернемся к цепным дробям, ибо в них прячется истин­ная бесконечность.

Пока что дадим стандартное книжное доказательство того, что корень из двух – число не рациональное. Проводится оно от про­тивного.

Предположим, что из них точно будет нечетным. Потому что если оба четные, значит, можно было еще раз сократить на 2.

Рассмотрим квадрат равенства (3):

 

Получим т ²  = 2п ² .

Это значит, что если на сетке нарисован квадратик с целочи­сленной стороной, то в нём количество единичных квадратиков такое же, как удвоенное количество квадратиков какого‑ то друго­го квадрата с целочисленной стороной (рис. 67).

 

Рис. 67. Что‑ то но получается нарисовать два таких квадрата. II это неспроста!

Значит, если К рациональное число, то т   ²   = 2 п   ²   верное равенство. Тогда т число четное, потому что оно делится на 2. Но если т делится на 2. то это значит, что т = 2к для некоторого целого числа к. Тогда т ²  = 4к ² .

Подставим в т ²  = 2п ²  значение для т ² . Получим 4к ²  = 2п ² .

Сократим на 2. получится 2fc² = п   ²   .  

Но тогда п тоже делится на 2. А значит, мы в начале этого про­цесса недосократили. Но мы же договорились досократить всё. что возможно. В этом и заключается противоречие с тем фактом.

что в выражении ‑ \/2 = Щ‑ можно добиться того, что хотя бы одно из чисел т, п будет нечетным.

То, что л/2 никогда не представляется в виде Щ, на самом деле означает то же самое, что равенство т ²  = 2п ²  всегда неверно. Никогда не получится взять один квадрат с целыми сторонами, умножить его площадь на два и получить другой квадрат с целыми сторонами (удвоенной площади). Ни для каких целых чисел.

Попробуем копнуть этот вопрос поглубже.

А может ли быть так, что они почти будут равны, например, т ² = 2n² ± 1?

Вдруг мы сможем взять какие‑ нибудь огромные числа, возве­сти их в квадрат, умножить одно из них на 2 и выяснить, что ре­зультаты отличаются на 1. Может ли такое быть или нет? И если может быть, то насколько часто такое бывает? И можно ли полно­стью описать все пары целых чисел (т, п), которые удовлетворяют уравнению т ²  = 2п ²  ±1? Вопрос, который ставился еще древни­ми – он называется «решение Диофантовых уравнений в целых числах».

Диофант жил в Александрии в III веке нашей эры. Он оставил после себя 13 томов математических изысканий, 6 из них худо­бедно, но дошли до нас, 7 – полностью и безвозвратно потеряны. 6 томов его изысканий до сих пор питают умы математиков. Дио­фант писал всё словесно. Примерно так: «Может ли быть такое, что одно число, будучи взятое то же самое число раз (то есть п · п ) и еще столько же раз (то есть 2п · п), отличалось бы от другого числа, взятого другое же число раз (то есть т ■ т) всего лишь на единицу? » Так он записывал уравнение

2п ²  = т ²  ± 1.

Можно ли такое уравнение решить в целых числах или нет? Мы пишем символами, поэтому далеко продвинулись в математике. Но все идеи буквально, буквально все подряд были в этих шести томах. Если чего‑ то в них не было, то, видимо, оно было в пропав­ших. Но мы уже не узнаем этого.

Диофант – человек, оставивший фантастическое наследие. В 1651 году Пьер Ферма читал книгу Диофанта по целочисленной арифметике. Читал и комментировал ее на полях. А сын Ферма издал книгу с комментариями своего отца. На полях был кладезь математических сокровищ. В частности, в одном месте было обна­ружено следующее. У Диофанта решалось в целых числах урав­нение а ²  + Ь² = с². То есть он пытался выяснить, может ли быть так, что все числа целые? Древним было хорошо известно, что та­кое может быть. Например, числа (3, 4, 5), и много‑ много других примеров.

Первое решение, возможно, даже имело практическое примене­ние 2, 5 тысячи лет назад. Берем веревку, делим ее на 12 равных частей, завязываем узелки в местах деления. После чего связы­ваем веревку в кольцо и делаем из нее треугольник так, чтобы на одной стороне было 5 узелков, на другой 4, а на третьей – 3.

И вот вы получили прямой угол кустарными средствами. Это очень важно.

Землемеру этого хватит. Всё. У него веревка с 12 узлами есть, и отлично. Но математик всегда хочет пойти до конца. Все ва­рианты найти, все целые а, Ь, с – такие, что получается прямо­угольный треугольник. Задача древнейшая. Ответ был известен еще древним индусам. «Пифагоровы тройки» – вот как называ­ются эти решения. Интересно то, что в этом месте слева на полях было написано рукой Ферма приблизительно следующее: «Вместе с тем, невозможно разложить никакой куб в сумму двух кубов, ни­какую четвертую степень в сумму двух четвертых степеней и во­обще никакую произвольную степень числа в сумму двух таких же степеней. Я нашел этому факту поистине удивительное дока­зательство, но на полях оно не поместится». Это – начало истории величайшей загадки математики – великой теоремы Ферма.

Ферма утверждает, что при п большем, чем 2, уравнение

 

х^п + у^п = zⁿ

не имеет решения в целых числах. То есть, конечно, можно взять х = у = z = 0. Или, если мы поставим х = 0, тогда у и z могут быть любыми одинаковыми. Но это всё неинтересно. А вот если ноль запретить, то если мы ищем среди положительных целых чисел х, у, z решения этого уравнения, то их нет, вообще нет. Ни одного, ни одной тройки (ж, у, z), ни для какого п, большего чем 2, то есть ни при п = 3, ни при п = 4, ни при каком п.

Эта загадка была страшно популярной среди широких масс на­селения – уж больно просто формулируется эта теорема (да еще какой‑ то чудак завещал крупную сумму тому, кто справится с до­казательством теоремы Ферма). Но и опытные математики были озадачены. Дело в том, что все утверждения, которые Ферма оста­вил без доказательства, оказались правильными (их все доказали после его смерти), а с этим творилось черт знает что: начали все сходить с ума, потому что всё кажется просто, и хочется взять ручку и начать писать. Вот вы мне не поверите, но когда мне было 10 лет, я этим занимался, честно. Но всё это безумие продолжалось только до 1994 года.

В 1994 году она была полностью доказана нашим с вами со­временником математиком Эндрю Уайлзом. На самом деле ему предшествовали 30 разных имен, которые долго в разных местах подстраивали большое здание. А он просто понял, в каком месте нужно сшить то, что уже известно. В частности, безусловную важ­ность здесь сыграла московская школа алгебраической геометрии. Последним был Уайлз, но в принципе это – всемирное творение.

Сейчас доказательство великой (или, как еще говорят, послед­ней) теоремы Ферма входит в книгу А. А. Панчишкина, Ю. И. Ма‑ нина «Введение в современную теорию чисел». Толстенная слож­нейшая книга по теории чисел, 7‑ я глава целиком посвящена тео­реме Ферма.

Ну а теперь фокус‑ покус, ладно? А то лекция уже кончается.

Берем нашу цепную дробь для «корня из двух»:

 

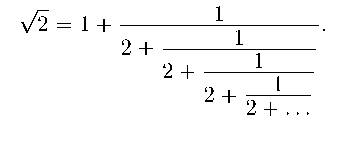
Обрубаем, получаем приближенное значение для корня из двух:

 

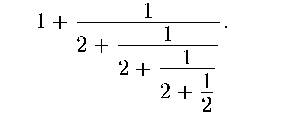
Такую дробь можно превратить в некоторое рациональное число, то есть в некоторое отношение двух целых чисел. Сейчас превра‑

не могу, так как квадрат; 5, 6, 7, 8 – могу, 9 – не могу, 10, 11, 12, 13, 14, 15 – могу, 16 – не могу, и так далее. Уравнение такого вида (см. подробнее об этом в следующей лекции) носит назва­ние уравнение Пелля. И, как обычно это бывает, Пелль не имеет к нему никакого отношения. В математике очень много фактов на­звано именами людей, которые никакого отношения к этому факту не имели. Шутки ради это явление математики тоже назвали «те­оремой». Вот, получилось так, что эту теорему назвали теоремой Арнольда. Она самоприменимая (то есть Арнольд не является ав­тором этой теоремы). Шутливую «Теорему Арнольда» придумал, вроде бы, Николай Николаевич Константинов и назвал теоремой Арнольда специально для того, чтобы она была самоприменимой, чтобы она тоже называлась не именем человека, который ее вы­думал, а другим. Математики мыслят логически, даже когда они шутят!

Давайте все‑ таки, чтобы вас убедить, пообрубаем эту дробь в разных местах. Смотрите. 1 – это ведь «1 разделить на 1». Если подставить в уравнение (4) т = n = 1, то что получится?

I² = 2 · I² ‑ 1

(то есть (4) выполняется).

Обрубаем дальше. Будет

Подставляем: 9 = 2 · 4 + 1.

Обрубаем еще раз. Получаем Подставляем.

49 = 2‑ 25 ‑ 1.

Вы видите, что теорема верна.

Гуманитарию уже не надо доказывать теорему, он уже «видит», что она верна. Но математику нужно ее доказать, нужно устано­вить, что это действительно всегда будет так. Мало того, оказыва­ется, что все такие обрубания дадут вам решения этого уравнения, и других решений в задаче нет. Вообще никаких.

Слушатель: Ну, или мы просто не нашли?

А. С.: Нет. Доказали, что больше не существует.

Ну, последний фокус‑ покус. Но берегитесь, он страшный. Знае­те ли вы, что такое бином Ньютона? Это – правило, по которому раскладываются выражения, в которых вы много раз умножили одну скобку на себя. В школе проходят (а + b)(a + b ) = а² + 2аЪ + Ь ² . Еще проходят: (а + Ъ)(а + Ь)(а + Ь) = а³ + 3а ² Ь + 3ab ²  + Ь³. Но есть некая формула, которая верна всегда, для любого количества ско­бок. Считается, что ее придумал Ньютон, но на самом деле ее, ско­рее всего, знали и до него. Просто он ее огласил. Так вот, бином Ньютона тоже помогает искать решения уравнения т ²  – 2п ²  = ±1. Ниже мы снова за К обозначим корень из двух.

Возьму (1 + К)² = 1 + 2К + 2 = 3 + 2К. Решением будет пара (т = 3, п = 2), и мы уже выше встречались с ним. Но, может, это случайно так совпало?

Возведение в куб вас должно уже убедить. Имеем:

(1 + К)³ = 1 + ЗК + 6 + 2К = 7 + 5К.

Не правда ли, это следующее решение нашего уравнения? Здесь т = 7, п = 5.

Возведем в четвертую степень. А это всё равно, что возвести два раза во вторую, один раз в нее мы уже возводили.

(1 + К)⁴ = (3 + 2К)² = 9 + 12К + 8 = 17 + 12К.

Проверяем:

17² = 289,

12² = 144,

144 · 2 = 288.

Получается: 289 = 288 + 1.

Это работает!

До встречи на лекции 4.

 

⇐ Предыдущая14151617181920212223Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: