Слушатели: 50 на 50.

А. С.: Да, правильно, девушки дорогие! Вот это вы правильно говорите. Либо встретите, либо не встретите. Правда? Значит, но­мер b либо принадлежит подмножеству В, либо не принадлежит. Сейчас я докажу, что не может быть ни того, ни другого. То есть сейчас я докажу, что вы не можете ни встретить крокодила, ни не встретить. Ни то, ни другое не может произойти. И это бу­дет то самое противоречие, которое будет устанавливать тот факт, что соответствия между множеством и множеством его подмно­жеств не бывает. Потому что оно выведено, исходя из того, что мы смогли устроить такое соответствие.

Поехали. Я утверждаю, что «инвентарный» номер подмноже­ства, которое состоит из таких натуральных чисел, что их соб­ственное подмножество их не содержит, не может ни содержаться в В, ни не содержаться в В. Предположим, что номер b содержится в В. Это значит, что он не может входить в множество тех чисел, которые в своих множествах не содержатся.

Слушатель: И значит, он не содержится в множестве В.

А. С.: И значит, он не содержится в В. А теперь представьте себе, что он не содержится в В.

Слушатель: Но тогда он должен содержаться, потому что он элемент В по определению множества В.

А. С.: Да. Тогда он должен содержаться в В. То есть если он со­держится, то он не содержится, а если он не содержится, то содер­жится. Теорема доказана методом «от противного», ибо мы при­шли к чисто логическому противоречию.

Вот она, математическая логика. Добро пожаловать! Каждый

й логик, как говорят, сходит с ума. Это мне говорил мой учитель, он тоже математический логик, но не шестой.

Делаем дальнейший вывод – это множество подмножеств больше, чем само множество. (Подсказка: во множестве всех под­множеств находятся все одноэлементные подмножества. ) Заманчи­вой является мысль, что это не только для подмножеств натураль­ного ряда чисел справедливо, но и вообще для подмножеств ЛЮ­БОГО множества. Но понятие «любое множество» так вдохновило некоторых математиков, что в ход пошли совершенно ужасающие множества типа «множество всех мыслимых множеств». (Или, на­пример, множество плохо совместимых слов «огород», «бузина», «Киев», «дядька» из известной поговорки. ) И возникли крупные математические проблемы с такими множествами. Но теория Кан­тора выдержала это нашествие «безумных множеств». Просто при­шлось внести необходимые уточнения в некоторые исходные поня­тия.

Вот еще один яркий образчик «безумных математических объ­ектов». Рассмотрим некоторый шар. Например, футбольный мяч. Есть способ разбить этот шар на конечное число кусков, из ко­торых потом можно будет составить ровно два шара такого же размера. То есть вы берете футбольный мяч, берете ножницы, раз­резаете мяч на несколько кусков, они совершенно безумно устро­енные, но все‑ таки куски. Потом кххх... и у вас два футбольных мяча. Всё. Математики – такие вот фокусники.

Слушатель: Такого же размера?

А. С.: Абсолютно такого же размера.

Другой Слушатель: Но это в теории возможно?

Слушатель: Только в теории и возможно. А на практике?

А. С.: А на практике ножницы должны быть устроены «неизме­римым образом», так сказать. Эти куски не имеют объема. Пред­ставление обычного человека о том, что любая объемная фигура имеет объем, не соответствует реальности. Далеко не у любой про­странственной фигуры можно посчитать объем. Далеко не у любой плоской фигуры можно вычислить площадь. Но вы не можете се­бе представить такую фигуру. Их выдумали математики. Фигуры эти страшные, и они никогда не возникнут ни в какой реально­сти. Но в теоретических построениях они есть, и без них вот нику­да. (А в процессе обучения такие «безумные» примеры позволяют лучше понять, как устроены окружающие нас РЕАЛЬНЫЕ пред­меты. ) На прямой, например, есть объекты, у которых нет длины. У каждой физической теории есть ареал, в котором она примени­ма. Механика применима для размеров порядка нас с вами, но она неприменима для размеров порядка атома, там она не работает. Там совершенно другая физика. В экономике макросистемы, ко­торые генерируют такие вещи как инфляция, безработица и так далее, они абсурдны для множества из двух, трех человек. И мое философское мнение, может быть, оно совершенно дилетантское, что у математики тоже есть ареал, но он находится в мозгу чело­века. Там вселенная совершенно другая, там нет воздуха, привыч­ной атмосферы нет. Математика тоже ограниченно применима, она не универсальна, она совершенно в другой области живет, поэтому в другой области нужно искать ограничения.

Слушатель: Как называется направление в математике, где можно разрезать шары таким невероятным образом?

А. С.: Теория меры. То, что мы называем площадью и объемом, математики называют мерой. Совершенно страшные объекты по­лучают меру, а некоторые не получают. Это очень существенно. Не любое множество можно измерить. В этом кроются границы того, что подсказывает нам наша интуиция. Она говорит про очень простые вещи, про многоугольники, многогранники, сферы, шары. Про что‑ то, достаточно просто устроенное. У чего всегда можно из­мерить объем, площадь. Если разрезать футбольный мяч на нор­мальные «человеческие» куски нормальным «человеческим» но­жом, то вы, конечно, никогда не получите двух футбольных мя­чей, просто из соображений объема. То есть идея в том, что объ­ема у тех кусков, которые участвуют в теореме, нет. Никакого. Ни нулевого, ни положительного, никакого нет. Но когда куски эти сложат вместе, у полученного мяча может быть вполне опре­деленный объем. («Объединение двух неизмеримых кусков может быть измеримым». )

А теперь я все‑ таки расскажу вам про алгоритм Евклида в гео‑

Q

метрических терминах. Давайте возьмем дробь j‑ j и превратим ее

 

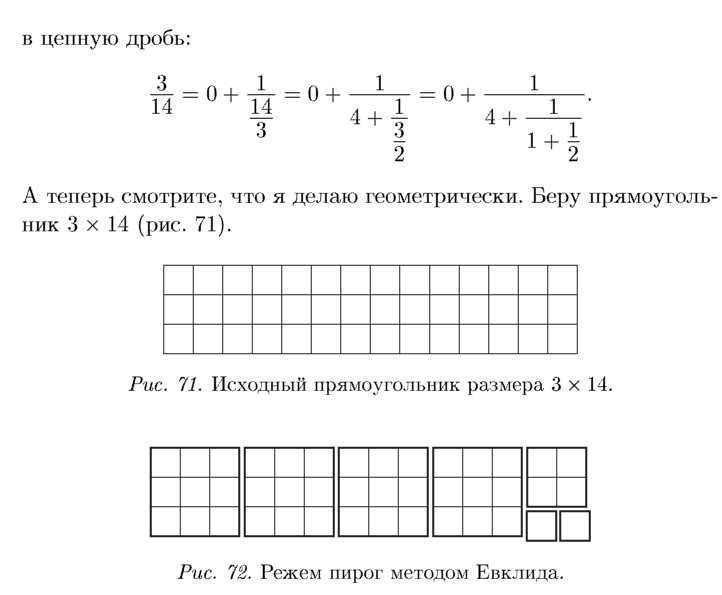
Отрезаю от прямоугольника квадраты (рис. 72). Остается пря­моугольник 2 на 3. Отрезаю от него квадрат. Остается 2 клетки. Вот они и есть наши целые части. 4 больших, 1 поменьше и 2 совсем маленьких.

Это и есть алгоритм Евклида. Такой красивый, геометрический способ.

Как показать на картинке, что рациональное число обязательно раскладывается в конечную цепную дробь? Рациональное число это как бы прямоугольник на клетчатой сетке. Потому, что у него

верх и низ целые.

10 Ч

Вот, скажем, это прямоугольник 105 в ширину и 13 в вы­

соту. 105 и 13 это целые числа, то есть у нас целое количество квадратиков. Теперь мы начинаем наш геометрический алгоритм Евклида. Отрезаем, пока можем, огромные квадраты 13 х 13, про‑

водим здесь границу это наша целая часть. Граница идет но це­лым клеткам, потому что отрезали целое количество квадратиков. Оставшаяся фигура целочисленный прямоугольник. Отрезаем квадраты от нее. Остается еще меньший прямоугольник. Понятно, что за конечное время всё будет вырезано. Каждый раз минимум один квадратик удаляется. Поэтому в какой‑ то момент квадрати­ки закончатся. Теперь вспомним фокус‑ покус, который я провел выше с числом «корень из двух» (точнее, с числом л/2 + 1, см. рис. 73).

 

Рис. 73. Прямоугольники, да по то... Стороны их несоизмеримы.

Начинаем делать ровно то же самое. Отрезаем квадратик (рис. 74). Потому что мы ищем, сколько раз единица укладыва­ется в «корне из двух плюс один». Она укладывается ровно два раза. Какие оказываются у этой конфигурации стороны? 1 и у/2–1. Тогда прямоугольник ABCD подобен BCD' А'.

 

Рис. 74‑ На горизонтальном прямоугольнике выделены два квадрата, остался кусочек, подобный исходному прямоугольнику.

То есть если мы перевернем и увеличим BCD' А' в некоторое количество раз, то получим ABCD. Доказательство нужно? Сей­час будет. Что такое подобие? Это «сильная похожесть» фигур. Углы у прямоугольников одинаковые, не хватает лишь пропорци‑ оналъности сторон. Анализируем, есть ли она. 1: (К + 1) равно ли (К – 1): 1? «Напоминаем, что К это корень из двух».

В прошлый раз мы доказывали, что это одно и то же. Подобие имеет место. Что же произойдет дальше? Если мы начнем даль­ше отрезать квадратики, мы опять получим подобие, и так будет до бесконечности (рис. 75).

 

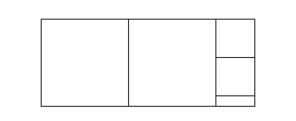
Рис. 75. «У попа была собака, он оо любил. Она съола кусок мяса, он оо убил в землю закопал, камень положил. На камне написал: “У попа была собака... ” и так далее до бесконечности».

Теорема доказана. Из‑ за подобия мы будем эту операцию бес­конечное количество раз проделывать, а значит, ни на какой сетке наш прямоугольник размеров (у/2   + 1) х 1 не может лежать и. следовательно, у/2   + 1 не будет рациональным числом.

Что‑ то это мне напоминает... В детстве у меня была книга. Она называется «Вот так история! ». Там был мальчик. Он ужасно себя вел. Все были воспитанные, а он был невоспитанный. И вот этого мальчика отправили в невоспитанный город, где у него сразу ста­рик отнял кровать, выгнал его. стал спать в этой кровати. Потом на его подушке выросло невоспитанное дерево, мальчика разбуди­ло. Его все стали обижать, на улице все толкались, и он попросился обратно. Просто детский триллер, да и только. На обложке этой книги, однако, была изображена нетривиальная картина.

Я на нее гляжу, гляжу... Это был момент, когда мой папа по­нял. что я математик. Я сам тогда ничего не понял, я был совсем маленьким. Я просто посмотрел на картину, на которой сидит де­душка и читает внуку эту книгу. А теперь представьте на секунду, что это означает? Это значит, что на маленькой книжке на кар­тинке изображены дедушка и внук, и у дедушки в руках та же книга, на которой изображены дедушка и внук. Я говорю: «Папа.

 

Рис. 76. На обложке книги сидел дед. Рядом сидели внуки. Дед держал такую же книгу, как исходная, но поменьше. А на ее обложке сидел дед (поменьше), внуки (поменьше), дед держал книгу (еще меньше). А на об­ложке дед (еще меньше... ). и так далее.

так это... Это же до бесконечности повторяется! Это же повтор, а значит, это должно быть до бесконечности, да? » В прямоуголь­никах (рис. 75) то же самое.

С этим связана еще одна интересная задача. Есть две карты города, разного масштаба. Одна карманная, другая большая настенная карта. Предположим, что кто‑ то взял, сорвал со сте­ны большую карту и кинул на нее маленькую. (Карты подобны по форме) (см. рис. 77).

Доказать, что можно взять иголку и проткнуть эти две карты в одной и той же точке изображаемого ими города.

Это вроде как игра. Я беру вот эти две карты и думаю, как бы мне положить верхнюю на нижшою. а вы приходите и иглой про­тыкаете. где захотите; если вы проткнули иглой одну и ту же точку (дом 37 по улице Профсоюзной), значит, вы выиграли, а если нет. то выиграл я. Теорема утверждает, что в этой игре проигрывает тот. кто кладет карту. То есть, как бы ни положить карты, всегда можно указать нужную точку.

Доказательство в одну строчку. Методом «взгляни и пой­мешь».

Рис. 11. Ничто по предвещало появления Ее величества Бесконечно­сти. ..

 

Нарисуем на маленькой карте ту территорию местности, кото­рую на большой карте закрыла маленькая карта.

Теперь нарисуем на нарисованной карте ту территорию, кото­рую она занимает на маленькой (рис. 78).

 

Рис. 18. II завертелись карты города аж до бесконечности!

Дальше они будут вертеться до бесконечности, но в пересечении всех этих карт будет точка. В нее и надо воткнуть иголку.

А теперь немножко сложнее: я беру две абсолютно одинако­вые карты города. Верхнюю снимаю, сжимаю, комкаю, склады­ваю. но не рву. Теперь кидаю на оставшуюся лежать карту так. чтобы верхняя не вылезла за пределы нижней (рис. 79).

 

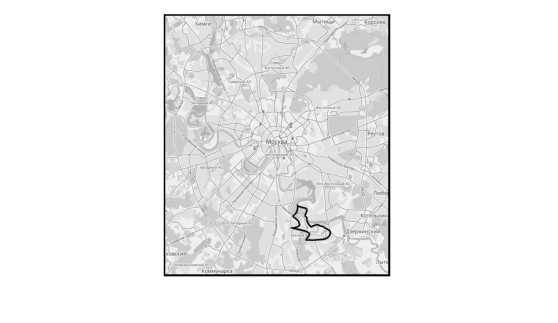
Рис. 79. Иллюстрация к теореме Брауэра.

Теорема. Всё равно можно проткнуть иголкой эти две карты в одном место. Всегда, что бы вы ни делали (единственное толь­ко нельзя резать и рвать). Если вы карту порвали, то можно добиться того, чтобы проткнуть было негде. А вот если мы не рва­ли. то всегда найдется общая точка, иногда их будет несколько, но одна найдется обязательно. При условии, что смятая до неузна­ваемости (и сплющенная) верхняя карта целиком лежит на ниж­ней. Эта теорема очень эффектна. На самом деле, она утверждает нечто про произвольное непрерывное отображение объекта в себя. Эта теорема не очень простая, я ее рассказываю на курсе «ма­тематика для экономистов» и в школе анализа данных Яндекса. Называется она Теорема Брауэра.

На самом деле, пока она не была доказана, в нее не очень вери­ли. Любое непрерывное отображение (разрешено всё. кроме раз­рывания) замкнутого выпуклого объекта (в теореме Брауэра го­ворится о замкнутом шаре) в себя всегда обладает неподвижной точкой. То есть точкой, которая никуда ни сдвинулась. Вы что‑ то растягиваете, что‑ то сжимаете, что‑ то складываете, но вы никогда, никогда не добьетесь того, чтобы все точки изменили свое поло­жение. Этого нельзя сделать. Этому есть математическое препят­ствие. и оно называется «теорема Брауэра о неподвижной точке».

* *

Вернемся к задаче, которой мы закончили предыдущую лек­цию.

(1 + х/2)², (1 + %/2)³, ... (1 + %/2)"

эти вот выражения почему‑ то тоже помогали нам решать урав­нение Пелля.

Сейчас как раз самое время открыть секрет. Заодно получим еще одно оправдание изучению уравнения Пелля:

ж² _ 2у ²  = 1.

Греки мыслили геометрическими образами. Старались увидеть чи­сло, увидеть теорему Пифагора. У них были «квадратные» и «тре­угольные» числа.

Например, 4 или 9 это квадратные числа (рис. 80).

ОО ООО ОО ООО ООО

Рис. 80. Из 4 или из 9 кружков можно сложить квадрат.

Что такое треугольное число? Это когда из такого количества кружочков можно треугольник собрать. 3, 6, 10 числа треуголь­ные (см. рис. 81).

_п О ° по ⁰⁰⁰⁰ ООО ООО О О О О

Рис. 81. Пород началом партии в биллиард шары укладывают в «тре­угольник».

Следующее 15, потом 21. Каждый раз прибавляем на 1 больше, чем в предыдущий раз.

Сам собой возникает вопрос: бывает ли так, что одно и то же число и квадратное, и треугольное? То есть количество фишек таково, что можно собрать из них квадратик, а можно перемешать и собрать треугольник.

Слушатель: Число 1 и такое, и такое.

А. С.: Безусловно. Человек, который говорит «число 1», облада­ет математическим мышлением. Не пропустить даже простейшего случая. Это очень важно.

Однажды я ехал в поезде из Иркутска в город Тулуп. И со мной в плацкарте ехала женщина с дочкой лет пяти. Мама явно не ма­тематик, но при этом хочет дочку чему‑ то научить. И она спраши­вает: «Вот, смотри. У тебя пять кукол. Как их можно разложить?

и 2». «Ну, да». «А еще можно как‑ нибудь? » Я с интересом наблюдаю. Тут дочка и говорит: «Можно 5 + О».

Я вскакиваю с полки, спускаюсь и говорю: «Ваша дочь имеет нетривиальные, очень хорошие математические способности».

Мама немножко помолчала, а потом согласилась. Но она не по­няла. Ведь назвать 5 + 0 может только человек, у которого четко развита логика, другой человек не назовет, это нетривиальный ва­риант.

 

Вернемся к треугольным и квадратным числам. Какое следую­щее, после 1? Следующее «и такое, и такое» число это 36 (см. рис. 82).

О

 

⇐ Предыдущая17181920212223242526Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: