Врезка 6. О бессилии «наблюдения» без «доказатель­ства»

Лекция 4

А. С.: На прошлой лекции я сказал кое‑ что про решение урав­нения вида х ²  – 2у ²  = ±1. Тогда обозначения были другие. Но на то это и математика, что «хоть горшком назови». В этой лек­ции переменные, значения которых мы ищем, будут обозначаться «ж» и «у». Теперь кое‑ что уточним. Можно взять вместо числа

любое натуральное число т и записать аналогичное уравнение: х ²  – ту ²  = ±1.

В принципе, почти ничего не изменится в общем ходе решения. Единственный вариант, при котором будут различия, это когда т представляется в виде квадрата натурального числа (4, 9, 16, 25... ), – тогда такое уравнение по неким очевидным причинам никаких решений, кроме ж = ±1, а у = О, не имеет.

В самом деле, попробуем найти нетривиальные решения урав­нения х ² ^9у ²  = ±1, то есть ж‑ ж = (3у)‑ (3у)±1. При «у», не равном нулю, получается, что квадраты двух целых чисел «ж» и «3у» от­личаются на единицу. Так мало они отличаться НЕ МОГУТ. Даже квадраты соседних целых ненулевых чисел (скажем, М и М + 1) отличаются больше, чем на 1, а именно: отличие их равно 2М + 1, причем М не равно 0.

Для всех остальных т прием, которым мы пользовались ранее при решении этой задачи, срабатывает. А прием этот был такой: нужно корень из т разложить в цепную дробь. То есть выделяем целую часть, потом «переворачиваем» оставшуюся дробную часть, получаем число, большее единицы, в нём опять выделяем целую часть, и так далее:

 

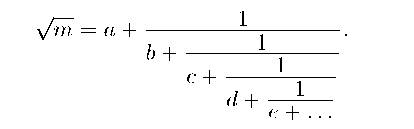
Я сказал в лекции 3, что для получения решения уравнения мы можем обрубить дробь в любом месте, привести к виду «це­лое число разделить на целое», и числа, которые получатся в чи‑

слителе и знаменателе, будут нашими решениями. И для т = 2 это действительно можно делать на любом месте. Но если это утверждение применить для других значений т, то получится, что я немного обманул вас. Есть теорема, доказанная Ж. JI. Лагран‑ жем, которая утверждает, что если мы разложим корень из числа, не являющегося квадратом, в цепную дробь, то цепная дробь на­чиная с некоторого места начнет повторяться. Появится период.

 

Врезка 6. О бессилии «наблюдения» без «доказатель­ства»

Понятие периода последовательности не такое простое, как хо­телось бы думать. Более того, это понятие демонстрирует бессилие прикладной математики для установления фактов чистой мате­матики. Например, допустим, что прикладной математик изуча­ет поведение следующей последовательности десятичных цифр: 2223222322232223. .. Что скажет при этом «совсем простой наблю­датель»? То, что имеется период «2223», состоящий из 4 цифр. Бо­лее «утонченный наблюдатель» возразит: не будем спешить, пона­блюдаем дальше за поведением этих цифр хотя бы до 34‑ го места. Сказано‑ сделано: получили

22232223222322237 22232223222322237...

Что, убедились?! Период‑ то имеет длину не четыре, а семнадцать! Но обиженный «простой наблюдатель» возразит: погодите радо­ваться. Понаблюдаем теперь хотя бы до сотого места. И увидели, что на 69‑ м месте (после семерки на 68‑ м месте) стоит не цифра 2 (как они оба ожидали), а цифра 0. Вот тут‑ то они призадумались... А есть ли вообще период у этой последовательности? И может ли «простое наблюдение» дать обоснованный ответ на этот вопрос? КОНЕЧНО, НЕТ! – скажет им чистый математик. Если у нас в ре­зультате наблюдения появилась гипотеза, что период равен 2223, то надо остановиться, проверить, есть ли научные предпосылки для доказательства этого (либо для опровержения этого), и про­должать исследование дальше. И если возможную длину периода не удалось определить или ограничить сверху никакими «наблю­дениями», это вовсе не означает, что последовательность неперио­дическая! Это означает, что пока что чистому математику не уда­лось решить эту проблему (может, потому, что он плохо ее решал).

Это, конечно, не означает, будто бы мы не доказали, что для разложения «корня из двух» период начинается сразу, и длина его равна единице, а сам период равен «2». В данном случае не про­сто повторяются числа 2222..., начиная со второго места, а повто­ряются условия   для повторения этого числа. Ниже мы не будем углубляться в эту философскую проблему, а просто предположим, что уже «кем‑ то» доказано наличие именно периода такой длины, и именно из таких чисел.

Мы раскладывали для самого простого случая, и в нём сразу пошел период: целые части со второго места равны 2, 2, 2, и т. д. Если бы я обрубал цепную дробь в любом месте для любого т, я совершил бы ошибку. А на самом деле обрубать нужно ровно в конце периода, то есть в том месте, где начинается повторение. Начало периода – это как раз самое большое число. В этом месте и нужно обрубать, игнорируя весь последний отрезок дроби, начиная с самого большого числа. Например, в идущем ниже примере мы доходим до 4 и обрубаем. В следующий раз можем обрубить перед второй четверкой, и т. д.

 

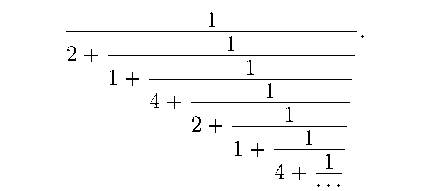
Но это был модельный пример, не относящийся ни к какому т.

Например, бывает, что повторение начнется на 7 или 8 ступень­ке дроби, или еще дальше. Число 61, среди первых 100 чисел, самое неприятное в нашем смысле. Ибо ‑ \/б1 очень долго раскладывается

в цепную дробь, пока не повторятся условия, обеспечивающие ци­клическое повторение всех выделяемых далее целых частей. И по­этому самые маленькие решения уравнения ж² – 61 у² = ±1 будут больше миллиарда.

В костромской области каждые полгода проводится школа для сильных школьников. Вот они у нас где‑ то за часик этот корень из 61 раскладывали. Потом еще минут десять сворачивали дробь, и на выходе получали два числа порядка миллиарда. Которые, если подставить в наше уравнение, чудесным образом дают реше­ние уравнения Пелля.

Цепная дробь (или алгоритм Евклида, который ее породил) мо­жет быть изложена геометрическим образом. Полезно знать, какая геометрия за этим стоит. Ниже я ее изображу.

Немного уточню теорему Лагранжа, что приблизит нас к тер­мину алгебраические числа. Что такое рациональное число? Мы договорились, что это «целое делить на целое» (то есть Щ ). Мож­но написать и по‑ другому. Рациональное число – это корень (то есть решение) уравнения т ^ пх = 0.

Например, ‑ g‑ – корень уравнения 17 – 5ж = 0. Подставьте

х = ‑ g‑ и проверьте это.

К чему мы приходим? К более широкому подходу. Рациональ­ные числа – это корни вот таких линейных уравнений, то есть уравнений первой степени с целыми коэффициентами.

Корнем какого уравнения является число «корень из двух» (обозначим его просто К)? Нужно написать выражение с иксом, у которого целые коэффициенты, такое, что при подстановке по­лучится 0. Вот оно: ж² – 2 = 0.

Оно 2‑ й степени. Вот я и говорю поэтому: К – число не рацио­нальное. Ведь это уравнение нелинейное, оно второй степени.

А если я напишу: ж¹⁰ ^3 = 0?

Что я получу на выходе? Корень 10‑ й степени из 3. Число не ра­циональное, удовлетворяющее уравнению, где слева стоит много­член с целыми коэффициентами.

Напишем произвольное уравнение 2‑ й степени: ах ² + Ьх + с = О (тут, конечно, «а» не равно нулю).

Такое уравнение вы, без сомнения, изучали в школе. Но вы из­учали его для произвольных а, Ь, с. А мы будем рассматривать только целые. То есть многочлен, в котором целое число раз взя­та единица (либо минус единица) – получилось «с», потом целое число раз взят х (с тем или иным знаком) – это будет «Ь», и це­лое число раз взят ж² (это – «а»). Решаем квадратное уравнение по известной формуле:

_ ± л/6² – 4ас ^Х  ~ 2а '

Мы получили выражение, использующее при своем построении операцию извлечения квадратного корня один раз. Так вот, теоре­ма Лагранжа звучит так: если х является решением уравнения

ах ² + Ьх + с = О

с целыми коэффициентами, то тогда его цепная дробь будет ли­бо конечной (если вдруг решение окажется рациональным), либо периодической. Верно также обратное утверждение. Если цепная дробь устроена так, что у нее, начиная с некоторого места, возника­ет периодическое повторение целых частей, то она удовлетворяет такому уравнению с целыми коэффициентами.

А вот теперь, опираясь на эту теорему, я могу вам дать основное определение. Число называется алгебраическим, если оно является корнем хотя бы одного уравнения с целыми коэффициентами про­извольной длины. Не обязательно квадратного, как у нас, а про­извольного (многочлен любой степени).

А трансцендентное число – это число, которое не является алгебраическим. С этим связана долгая история. Стоял вопрос, существуют ли трансцендентные числа вообще. Древним грекам было известно, что длина диагонали квадрата не является рацио­нальным числом. Это было очень неудобно древним. Но, с другой стороны, она удовлетворяет элементарному квадратному уравне­нию, то есть является алгебраическим числом. Возникает вопрос: все ли числа алгебраические? Ответ – нет. Математик Ж. Ли‑ увилль, живший в середине XIX века, просто выписал конкретное число и доказал, что оно не является алгебраическим. С этого всё и началось. На самом деле алгебраических чисел неизмеримо меньше, чем не алгебраических, то есть трансцендентных.

Грубо говоря, если вы возьмете вещественную ось и случайно воткнете в нее булавочку нулевой толщины, вы практически на­верняка попадете в неалгебраическое число.

Мы с вами на 3 лекции какую‑ то задачу решали с какой‑ то железкой (помните? – которую надо куда‑ то отправить, чтобы она встала в вертикальное положение). Если вы эту железку на­угад взяли где‑ то, со свалки, установили на шарнир и стали отпра­влять ровно с той силой, чтобы она за бесконечное время встала в вертикальное положение, то сила, наугад взятая, будет транс­цендентная. На самом деле сама железка тоже будет трансцен­дентной по своей длине. Есть самая большая загадка, которая обычно совершенно не понятна людям, не занимающимся мате­матикой. Как это – бесконечности могут быть разные? Вот как можно представить, что бесконечности разные? Вроде бесконеч­ность, она и есть бесконечность. Они все одинаковые. Это один наивный взгляд. Другой наивный взгляд на вещи состоит в том, что, наоборот, почти все бесконечности разные. Вот, скажем, возь­мем множество всех натуральных чисел и множество всех целых чисел. Каких больше?

 

⇐ Предыдущая15161718192021222324Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: