Теперь разберем задачу про футбол (рис. 87).

С каким минимальным количеством баллов можно выйти из группы в следующий раунд? Ниже приведен пример, когда это ко­личество равно четырем (рис. 87, справа).

 

Рис. 87. Слова: Матчи команд самих с собой но имеют смысла. Справа: финальные счета в матчах, где А всех победил, в то время как прочие игры сыграны вничыо.

Итак. «А» выигрывает все игры. Все остальные матчи сыграны вничыо. (Напомним, что за победу дается 3 очка, за ничью 1 очко, за поражение 0. )

Получается, что выходит из группы в следующий раунд лучшая команда «А» и еще одна из команд с 4 баллами. Я не знаю, было ли такое в лиге чемпионов, но с 6 баллами точно выходили.

Встает другой вопрос. Как доказать, что с 3 баллами выйти не­льзя! Конечно, можно было бы перебрать все З¹² вариантов розы­грышей матчей (ибо имеется 12 незаполненных мест, и на каждом месте может быть 3 различных исхода). Но хотелось бы этого из­бежать. Давайте попробуем формально рассуждать. Как мы будем это делать? От противного. Предположим, что какая‑ то команда вышла с 3 баллами. Какие в этом случае количества баллов мо­гут быть у всех команд? Вышеуказанный вариант для команд А,

В, С, D был 18, 4, 4, 4. Если какая‑ то команда вышла в следующий раунд с 3 баллами, значит, как минимум у двух команд должно быть тоже не больше 3 баллов. Потому что иначе наша команда не вышла бы из группы. Раз она вышла, следовательно, у двух других команд баллов меньше или равно 3.

Вопрос: сколько баллов у команды, которая больше всех на­брала?

В каждом матче разыгрывается суммарно или 2, или 3 балла (ничья дает 1 + 1, победа дает 3 + 0). Поэтому за все матчи все ко­манды могут набрать минимум 2 · 12 = 24 балла, если все сыграли вничью, максимум – 3 · 12 = 36, если каждый матч был выигран.

В нашей ситуации три команды набрали не более, чем по 3 бал­ла, в сумме 9, значит у четвертой команды не меньше 21 – 9 = 15 баллов.

Значит, она выиграла почти все матчи.

Давайте уточним, как команда могла набрать 3 балла. Она либо три раза сыграла вничью, либо один раз выиграла. Больше спосо­бов нет. Одна победа и 5 проигрышей, либо 3 ничьих и 3 проигрыша. Обозначим это так:

Вариант 1. Н

либо

Вариант 2. 0 0 0

Слушатель: Это значит, что 18 очков в розыгрыше.

А. С.: Рассмотрим вариант 1. В 6 матчах было разыграно 18 оч­ков, значит, в оставшихся 6 матчах будет не менее 12 баллов, так как в каждом матче разыгрывается не менее 2 баллов. Значит, в сумме получается не меньше 30 баллов. Значит, у четвертой ко­манды не менее 30^9 = 21, чего быть не может, так как максималь­ный результат любой команды равен 18, то есть все выигранные матчи.

Итак, вариант с одним выигрышем отпадает. Рассмотрим дру­гой вариант: три ничьи.

Вариант 2. Четвертая команда набрала не меньше 15 баллов (минимальное количество 24, три команды набрали в сумме 9, получаем 21 – 9 = 15). Значит, она одержала минимум 5 побед. (Меньше не может быть, так как всего 6 матчей. Даже если 4 по­беды и 2 ничьи, получится 4 · 3 + 2 15).

Получается минимум, который команды могли набрать вместе: не 24, а 29 (ибо пять матчей с победами принесли 15 очков, а остальные 7 матчей – не меньше 14 очков). Значит у четвертой ко­манды минимум 29^9 = 20 баллов. 20 18, где 18 – максимально возможное количество баллов. Противоречие.

Другой вопрос, так сказать, «обратный» к первому. С каким максимальным количеством очков можно не выйти из группы в следующий раунд?

Слушатель: 12.

А. С.: Да. И как должна быть устроена таблица? Одна команда (скажем, команда D) всем проиграла – 0 очков. Остальные 3 ко­манды выигрывали по кругу: А у В, В у С, С у А. Тогда у трех команд будет по 12 очков. И одна из них должна будет покинуть чемпионат.

Почему нельзя не выйти в следующий этап с 13 очками? Пред­положим, что вы набрали 13 или больше очков, почему вы точно знаете, что вы вышли в следующий этап?

Подсказка. Если бы кто‑ то с 13 баллами не вышел, то две ко­манды, которые вышли, имели бы не меньше, чем 13.

Теперь поговорим о том, с какой горы на сколько кило­метров видно.

Я залез на Хибинские горы, могу ли я видеть Мурманск, ко­торый находится на расстоянии 100 км от гор? Ответ: на самом горизонте – смогу (если сопки около Мурманска не помешают).

Сейчас мы получим точную формулу для максимальной види­мости.

Уже первые шаги вверх от земли сразу дают очень большую видимость.

С поверхности ничего не видно. Ноль, он и есть ноль. Горизонт стянулся в точку. Чуть‑ чуть выше нуля поднялись, на 10 санти­метров, и сразу видно примерно на километр (это если Земля – идеальный шар). Обозначим высоту горы за h. Расстояние до цен­тра земли обозначим за R и 6400 км. Эта числовая величина нам также пригодится, когда мы будем решать задачу про Алису.

Посмотрим на рис. 88. Я хочу знать, чему равно L, то есть на сколько километров видно? Здесь есть одна тонкость.

 

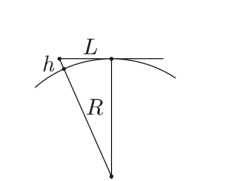
Рис. 88. Земля в разрезе. Расстояние от центра до вершины горы R + /;. расстояние от центра до точки касания R. Через L обозначено расстояние от вершины до точки касания.

Вдали будет горизонт. А вот если с другой стороны (за горизон­том) имеется такая же гора высоты h. то ее видно вдвое дальше. А если там гора высоты ^ то всё равно гораздо дальше, чем просто до горизонта (рис. 89).

 

Один раз при мио па Байкале видный ученый совершил детскую ошибку. Он сказал: «Мы никак не можем видеть горы, которые на­ходятся в районе Улан‑ Удэ. Не можем, потому что... » и даль­ше привел вычисления по формуле, которую мы сейчас выведем. Я говорю: «Ты не учитываешь, что мы сами сейчас не на Байкале, а на сильном возвышении». «О... ». говорит: «Конечно, это всё удваивает». На Байкале очень здорово наблюдать, что Земля круглая. Племена, которые жили на Байкале, наверняка издавна знали, что Земля круглая.

Помните теорему Пифагора? У нас образуется прямоугольный треугольник с гипотенузой R + h и катетами R и L. Значит.

(R + /г)² = R ²  + L ² .

 

R² + 2 Rh + К² = R² + L².

Страшная величина (квадрат радиуса Земли) сокращается, и оста­ется:

 

I² = h² + 2 Rh.

Здесь нужно быть не только математиком, но и физиком для то­го, чтобы сказать, что К ², в общем‑ то, равно нулю.

Потому что по сравнению с двойным радиусом земли Н ²  очень маленькое число. Это вещи несопоставимые, в том смы­сле, что первая подавляюще больше, чем вторая. Поэтому, чтобы без лишних усилий оценить, на сколько километров видно, доста­точно положить Н ²  = 0 и написать:

 

l = Vmh.

Что здесь важно понимать? Что 2R величина постоянная, ко­рень из нее равен 113. А если совсем грубо то просто 100.

Есть такая оценочная формула:

= mVh,

\fh эта функция, которая сначала очень быстро возрастает, а по­сле отхода от нуля увеличивается медленно (см. рис. 90).

 

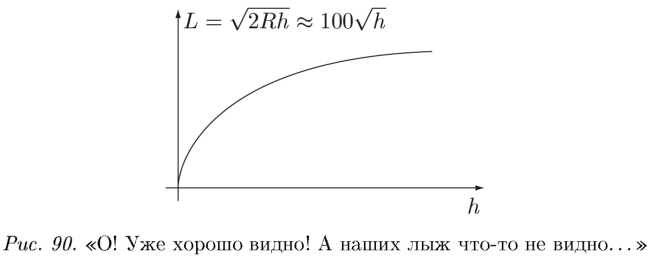
Чуть‑ чуть h отлично от нуля, прямо самую малость, а корень уже очень большой. Поэтому и получается, что вы чуть‑ чуть под­няли голову от Земли и: «О! Уже хорошо видно! » Давайте немного покрутим эту формулу.

Вот при h = 1 км с Хибин видно на 100 км, а более точный результат – действительно – на 113 километров. 113 километров вполне достаточно, чтобы увидеть Мурманск с Хибинских гор.

Слушатель: То есть на один градус, а точнее, на 1, 0128 гра­дуса.

А. С.: Да, на один градус. С километра видно на 1 градус.

 

⇐ Предыдущая19202122232425262728Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: