равновесие, центр тяжести этой системы должен лежать ниже точки опоры.

А теперь рассмотрим ситуацию, когда у качелей вместо спинок есть держалки для ног (рис. 100).

Пусть опять подул ветерок, и качели наклонились. Опять изме­нились плечи, только увеличилось то плечо, которое сверху. По­этому качели потянет вниз, обратно к горизонтальному состоянию равновесия. А дело в том. что теперь центр тяжести НИЖЕ точки опоры (сами поймите, почему).

Но самое интересное, почему качели без спинки и подножки всё равно находятся в наклоненном виде? Здесь и без теоремы ясно.

Дело в том. что у доски есть толщина. И когда качели наклоня­ются. одно плечо получается на маленький треугольничек больше, чем другое (см. рис. 101).

Он‑ то и перевешивает качели в сторону.

* *

А теперь нерешенные проблемы школьной математи­ки. Но прежде я хочу рассказать о том. как мыслят математики.

как они решают задачи. Есть такой английский принцип: «Think out of the box», то есть «Подумай, не выглянуть ли за пределы исходного ящика». Давайте посмотрим, как он работает.

Задача:

На плоскости даны три различные по радиусам окружности, не пересекающиеся друг с другом. К каждой паре окружностей проведена пара внешних касательных, и отмечена точка их пере­сечения (см. рис. 102). Лежат ли три отмеченных точки на одной прямой?

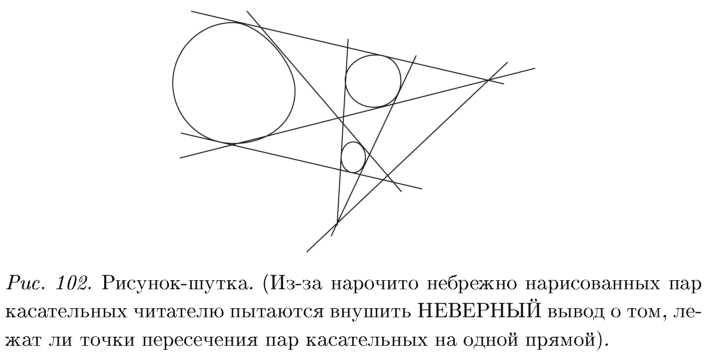
ОТВЕТ: : точки пересечения касательных лежат на одной пря­мой.

А как же быть с рис. 102? Он что. нас обманывает? Да!!! С ри­сунками это часто бывает. Поэтому делать выводы надо не после беглого взгляда на рисунок, а после строгого математического до­казательства (или строгого опровержения).

Доказательство состоит в следующем. Рассмотрим три полу­сферы. которые пересекаются нашей плоскостью по своим боль­шим окружностям. Представьте себе 3 сферических купола боль­шого. среднего и малого радиуса.

Эти 3 сферы сверху накрываются постепенно опускающейся вниз горизонтальной плоскостью, пока не произойдет касание са‑

мого большого купола. (Такая плоскость ровно одна. ) Теперь (гля­дя на рис. 102 и мысленно выходя за пределы исходной плоскости) будем «вертеть» получившуюся плоскость до тех пор, пока она, оставаясь касательной к большому куполу, не коснется среднего купола; затем вертим ее дальше (не теряя точек касания с боль­шим и средним куполом), пока она не коснется малого купола. Та­кая «трижды касательная плоскость» уже ровно одна (здесь надо предполагать, что центры окружностей не лежат на одной прямой). Так вот. После очень простых соображений становится очевидно, что наши отмеченные точки лежат в этой новой плоскости.

(ПОЯСНЕНИЕ. Считая, что рис. 102 нарисован не на плоскости, а в пространстве, содержащем исходную плоскость, представьте себе, что вместо пары внешних касательных мы нарисовали конус, внутри которого «спрятались» касающиеся этого конуса сферы. Таких конусов будет ТРИ. Вершина каждого из них находится (как нам подсказывает «пространственное воображение») как раз там, где находятся отмеченные в условии задачи точки. )

Но отмеченные точки также лежат и в исходной плоскости. Зна­чит, они лежат на прямой пересечения этих плоскостей. Теорема доказана.

Я сейчас пояснил, как думают математики. Это задача никаким простым методом не решается без выхода в пространство. Выход в пространство решает ее в один ход. Так происходит с математи­кой. Идея – выйти за пределы того, что у вас дано. Математи­ка – это выход за пределы. Все великие открытия, все великие доказательства связаны с покиданием пределов изученного, пре­делов данного и требуемого в задаче.