Основная теорема о построениях циркулем и линейкой

‑ 0, 5 0, 5 1, 5 2, 5

 

‑ 10 12 3

А если я еще раз разделю пополам? Я могу нарисовать, где жи­вут числа, полученные из целых делением на 3, на 5, на 1000 и т. д. Но удивительным фактом, который был известен уже древним, является то, что не все числа можно представить в виде дроби. Например, я построю квадрат со стороной 1 и возьму его диаго­наль. Ни одна обыкновенная дробь не равна длине диагонали ква­драта. Заметьте, что число, равное диагонали квадрата, строится циркулем и линейкой (так как сам квадрат циркулем и линейкой мы построить можем).

Но оно не является рациональным числом. Это было помещено в первой части книги. То есть мы умеем теперь строить квадратные корни, потому что диагональ квадрата выражается квадратным корнем.

Любое рациональное число можно построить циркулем и линей‑

кой. Давайте, например, построим –Знак минус просто означа­ет. что число надо откладывать не вправо от нуля, а влево. Чтобы

1 построить достаточно построить ^ и отложить этот отрезок

раз. А чтобы построить у. придется использовать очень удоб­ную: теорему Фалеса (которая изучается в школе). Сейчас мы ею воспользуемся.

 

Теорема Фалеса (в простейшей формулировке). Если на одной из двух прямых в плоскости отложить последователь­но несколько равных отрезков и через их концы провести парал­лельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные отрезки (рис. 117).

 

Рис. 117. Дво прямые (горизонтальная и наклонная) выходят из начала координат и поросочоны системой параллельных прямых. Если на одной из прямых мы отсекли равные отрезки, то на другой прямой отрезки тоже будут равны между собой (Теорема Фалеса).

Мне дан единичный отрезок. Отложу его по горизонтальной оси от начала координат и проведу произвольную наклонную прямую (тоже из начала координат) (рис. 117).

На этой прямой отложу от начала семь равных отрезков (не­важно. какой длины) и конец последнего отрезка соединю с концом единичного (горизонтального) отрезка.

После этого провожу прямые, параллельные той. что соединила концы горизонтального (единичного) отрезка и наклонного отрез­ка. и проходящие через конец предпоследнего из семи отрезков; затем через конец пред‑ предпоследнего. и так далее.

По теореме Фалеса получается, что все получившиеся на гори­зонтальном единичном отрезке кусочки равны друг другу то

есть мы получили

Корень строится немножко сложнее. Беру произвольное число

а, которое я уже построил циркулем и линейкой и из которого

 

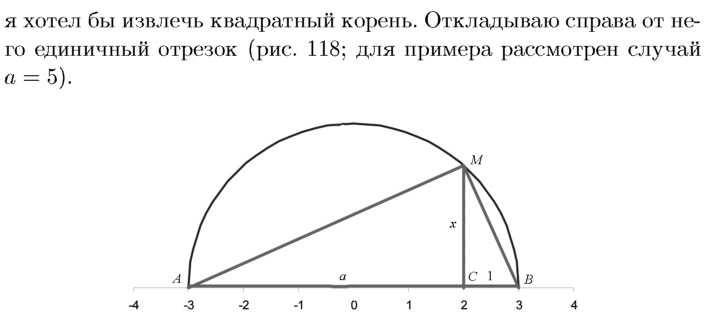
Рис. 118. Отрезок и = 5 отложен между х = –3 и х = 2; единичный отре­зок между х = 2 и х = 3. Строим полуокружность радиуса 3. Проводим перпендикуляр из точки х = 2 до точки пересечения с окружностью. Это и есть отрезок длины \/5. Все три треугольника прямоугольные, и все они подобны друг другу.

Теперь я рассматриваю новый отрезок длины а + 1 как диаметр окружности. Делю его пополам (это мы делать умеем) и строю верхнюю полуокружность.

Из точки х = 2 (отделяющей отрезок «а» от отрезка 1) восста­навливаю перпендикуляр. Получаю отрезок с концами на окруж­ности и отрезке.

 

Теорема: длина полученного отрезка равна \/5.

Доказательство. Обозначим за А и В концы диаметра, за М и С концы проведенного нами перпендикуляра (С ниже, чем М). Треугольник АВМ подобен треугольнику AM С, так как у них острые углы совпадают, а один из углов прямой. (Угол АМВ прямой, как и любой угол, вписанный в полуокружность. ) Значит, и третьи углы равны. По той же причине и треугольник АВМ подобен треугольнику МВС. Значит, можно записать отношение катетов малых треугольников

_ х

 

х а

(где «ж» – длина проведенного нами перпендикуляра); ж² = а, ж = л/а, что и требовалось доказать.

Теперь мы умеем строить всякие страшные «многоэтажные че­моданы». Любое выражение, которое является результатом конеч­ного числа операций плюс, минус, умножить, делить и взять ква­дратный корень, можно построить циркулем и линейкой. Напри­мер,

 

Основная теорема о построениях циркулем и линейкой

утверждает, что верно и обратное: то есть если какую‑ то точку удалось построить циркулем и линейкой, то координаты этой точ­ки должны быть получены с помощью конечного числа опера­ций плюс, минус, умножить, разделить и взять корень. Но есть точки на прямой, которые таким образом не выражаются, а зна­чит, и не строятся при помощи циркуля и линейки. Так, число ж не является результатом конечного числа таких операций (ни мил­лиона, ни миллиарда! ), и, следовательно, построить его невозмож­но. Доказательство этого факта придумали только в конце XIX ве­ка.

Более чем полвека назад, в начале XIX века придумали до­казательство задачи о невозможности трисекции угла с помощью циркуля и линейки. Идея его такая. Если можно разделить любой угол на три части, то мы могли бы построить угол в десять граду­сов (так как угол в 30 градусов мы построить можем). Но тогда, конечно, мы могли бы построить отрезок, длина которого равна sin 10°.

Рис. 119. sin 10° построить нельзя. Это вам но какой‑ нибудь sin 72°!

 

Но доказано, что это число построить нельзя. (Если выразить sin 10° через sin 30°. то получится кубическое уравнение, а для по­строения его решения необходимо уметь строить кубический ко­рень. К сожалению, с помощью циркуля и линейки этого сделать нельзя. ) Мы пришли к противоречию, значит, задачу о трисекции угла решить невозможно.

Третья великая задача древности удвоение куба. Вам дан кубик. Нужно построить кубик вдвое большего объема.

Если у исходного куба сторона равна единице, то какая сторона у удвоенного куба? Объем исходного куба равен 1. значит, у удво­енного он равен 2. По формуле V = а: ³  получаем, что сторона куба должна быть v^2. Поэтому задача, на самом деле, очень просто формулируется. Построить корень кубический из двух.

Сделать это циркулем и линейкой невозможно. По тем же со­ображениям. почему нельзя произвести трисекцию угла. (Как ни странно, число \/2 циркулем и линейкой построить можно! Уга­дайте. как? ) Лет сто назад еще так мало было известно о числах, что математики не имели ответа на самые очевидные вопросы:

например, иррационально ли число \/2^? 25 Приходилось чуть ли не по отдельности перебирать такие числа и разбираться с ними.

Весьма трудным оказалось и число 7г, потому что до конца XIX века не было понятно, как оно устроено.

У четвертой великой проблемы, которая была оставлена древними, особенно интересная судьба. Какие правильные много­угольники строятся циркулем и линейкой? Про нее мы говорили чуть раньше и сейчас еще немного поговорим. Древние умели стро­ить правильные треугольники, четырехугольники, пятиугольники, шестиугольники и их «производные». Например, десятиугольник или двенадцатиугольник. А вот семнадцатиугольник не умели. Его построил в 1796 году 19‑ летний (обратите внимание! ) Карл Фрид­рих Гаусс. Процедура достаточно сложная. Не буду скрывать. Не­который секрет состоит в том, что построение нельзя придумать, не зная, что такое комплексные числа. Комплексные числа – это такая волшебная палочка. У шаманов есть бубны, а у математи­ков – комплексные числа. Это такая числовая структура, кото­рая помогает на ура решать задачи, кажущиеся нерешаемыми. Ну, при чем здесь комплексные числа, когда мы говорим о семнадца‑ тиугольнике? Тем не менее семнадцатиугольник строится толь­ко с применением комплексных чисел. Впоследствии (в 1836 г. ) Пьер‑ Лоран Ванцель выявил критерий возможности построения правильного многоугольника. Оказывается, строятся только такие правильные р‑ угольники (где р  – простое число, то есть делится только на единицу и на себя), для которых «р» может быть запи­сано в виде

2²’* + 1 (где к = 0, 1, 2, 3,... ).

Например, простое число 17 удовлетворяет этой формуле, если взять к = 2.

В заключение дам вам простую задачу. Докажите, что если есть некоторое простое число р и простое число q, и можно построить р‑ угольник и q‑ угольник, то можно построить и pq‑ угольник.

Наконец, вот третий сюжет, который мы рассмотрим: постро­ение одной линейкой. Циркуль отменяется. Есть только линейка. Здесь всё еще веселее. Казалось бы, с линейкой многого не достиг­нешь: она может лишь соединять две уже данные точки прямой!

А водь ость небезынтересные задачки. Например: на плоскости да­на неравнобочная трапеция. С номощыо одной линейки разделить пополам верхнее и нижнее основание этой трапеции. Здесь, кажет­ся. совсем не за что ухватиться. Ну. проведем две диагонали в этой трапеции. Ну. продолжим боковые стороны трапеции до пересече­ния. Получили две новых точки. Ну. соединим их тоже. А даль­ше что?

Оказывается, больше ничего. Последняя из построенных пря­мых аккуратно делит оба основания пополам. Да только как это доказать?

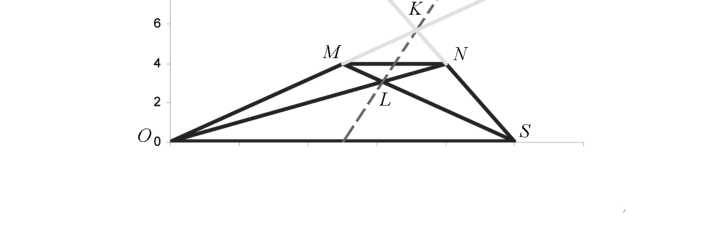
Докажем это «методом Декарта». Разместим эту трапецию в до­статочно удобной системе координат на плоскости (рис. 120).

ю

8.

 

О 2 4 6 8 10 12

Рис. 120. Для решения задачи проведены 5 очевидных прямых, послед­няя из которых (пунктирная) как раз и разделит оба основания пополам.

Как следует понимать выражение «удобная система»? Ну. на­пример. такая: весь объект целиком лежит в первой четверти, как можно больше вершин лежат на оси иксов, а одна из них является точкой (0. 0). Сам объект задан при этом несколькими параметра­ми. через которые легко выразить различные части объекта, а так­же можно отразить некоторые особенности расположения частей объекта.

при подстановке у = 4 и у = 0 даст абсциссы построенных то­чек. Они окажутся равными 6. 5 и 5 соответственно и разделят оба основания нашей трапеции аккурат пополам!

Разобранная выше задача когда‑ то давалась на школьных олимпиадах примерно для 7 класса. Но когда «широкие массы абитуриентов и репетиторов» познакомились с методом ее реше­ния, кто‑ то додумался, как ее «слегка изменить» и дать для 10 класса.

Задача. Дана неравнобочная трапеция. С помощью одной ли­нейки разделить нижнее основание на 41 равную часть.

Решение этой задачи тесно опирается на решение предыдущей и вполне может быть найдено школьником 7 класса. Делим оба основания пополам, затем тем же методом – на 4 равные части. А потом на 8 равных частей, и т. д., пока не получим 64 равных части (и на верхнем, и на нижнем основании). После чего дела­ем замечательный трюк: на верхнем основании отсчитываем ров­но 41 часть из 64 и проводим линейкой НОВУЮ БОКОВУЮ ЛИ­НИЮ. Получилась новая трапеция, у которой верхнее основание аккуратно разделено на 41 равную часть. Соединяем точки деле­ния верхнего основания с точкой пересечения боковых сторон но­вой трапеции. Получится 40 прямых линий, продолжения которых аккуратно делят на 41 равную часть нижнее основание.

Видите, какие «волчьи ямы» нам готовят на олимпиадах. Но мне досталась еще более плохая. В ней даже не было точек, через которые можно провести прямые. Прямые надо было проводить наобум, но ответ при этом получить не «наобумный», а вполне конкретный.

Расскажу про эту очень красивую задачу. Я получил ее на экза­мене по геометрии в 11 классе школы № 57. Мой учитель дал мне эту задачу: нарисована окружность и дана точка вне этой окружности (рис. 121).

Построить с помощью линейки касательную к окружности, проходящую через данную точку. Дальше случилось следующее: я нарисовал, как это делать, но, по некоторой причине, доказать

 

Рис. 121. Води прямые «туда, но знаю куда» и построй касательную.

по смог. (О причине я вам скажу позже, это будет детективная история. ) Я получаю за экзамен три балла, а учитель алгебры говорит: «Нет. наверное, у Савватеева было помрачение... давайте четыре поставим».

Давайте посмотрим.

Дана линейка, окружность и точка. Что делать? Можно про­вести несколько прямых, «секущих» окружность. Я провел три прямые «почти наобум» и получил шесть точек на окружности. Затем их накрест соединил и получил еще две точки (рис. 122).

 

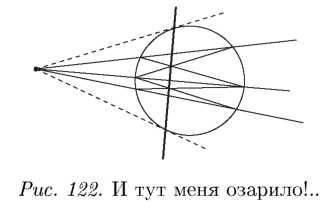
Дальше я соединил эти точки, и мне «внутренний голос» под­сказывает. что точки, которые получились на окружности, как раз и есть точки касания.

Да. говорит мне экзаменатор. это правильная конструк­ция. Докажи. Докажи, что это точки касания.

Что такое касание в терминах геометрии? Касание прямой и окружности в терминах школьной геометрии означает, что пря­мая и (полная) окружность пересекаются в одной точке. Имеют одну общую точку. Как же это можно доказать? Сейчас я вам по­кажу такое доказательство, что у вас от него пойдут по коже му­рашки. Но. во‑ первых, на экзамене я его не дал; а во‑ вторых, надо

сделать предварительные пояснения, что такое «проективные пре­образования» (не входящие в общеобразовательный курс обычной средней школы). Ну и, кстати, это же обоснование можно было сде­лать обычным «методом Декарта» (то есть, рассмотрев некоторую систему прямоугольных координат). Правда, при этом останется «за кормой» истинная красота решения этой задачи.

Врезка 10. Проективная геометрия – новый мир мате­матики

Что такое «проекция», знают многие. Это – тень, которая от­брасывается на плоскость предметом, освещаемым точечным ис­точником света – либо находящимся недалеко (и тогда лучи све­та, исходящие из него, расходятся), либо лежащим на бесконечном расстоянии (тогда лучи света параллельны). Пример для первого случая – свет небольшой настольной лампы. Для второго – сол­нечный свет. Однако тень от непрозрачного предмета может при­вести к заблуждению. Например, можно изготовить такой пред­мет, от которого тень, отбрасываемая вдоль оси X, имеет форму квадрата, вдоль оси Y – форму круга, а вдоль оси Z – равно­бедренного треугольника. Чтобы изготовить такой предмет, возь­мите деревянный цилиндр (с высотой, равной диаметру) и акку­ратно стешите топором с двух сторон дерево так, чтобы снизу остался круг, а сверху он превратился бы в отрезок, по длине равный диаметру круга. Поэтому при практическом применении проективной геометрии возникает проблема, как рисовать пунк­тирные линии, чтобы лучше понять структуру изучаемого пред­мета и в то же время не сильно загромоздить чертеж этими лини­ями.

Когда математики попытались дать себе более ясное предста­вление о том, что же такое есть «проекция», они ужаснулись. Оказалось, что тенью от окружности может служить не окруж­ность, а эллипс («сплющенная окружность») и даже просто отре­зок. И длина этого отрезка может быть больше диаметра окруж­ности. Но это были еще только цветочки. Оказалось, что проекци­ей эллипса может оказаться... бесконечная кривая, называемая «ветвь гиперболы». Таким образом, понятие проекции неизбежно включало в себя бесконечно удаленные точки (и они спокойно мо­гли переходить в обычные точки, и наоборот). Но тогда возник во­прос – в каком же «мире» мы изучаем проективную геометрию: на прямой, на плоскости, в пространстве? Ответ: не на прямой, а на проективной прямой. Она получается из обычной прямой до­бавлением одной новой точки: бесконечно удаленной. Казалось бы, от этого добавления прямая оказалась «еще более бесконечной» (ведь она была бесконечной и без добавления новой точки). Но, как выяснили топологи, полученный объект по своим свойствам совпадает с обычной окружностью. А ведь ее мы не считаем бес­конечной!

Второй вопрос: а как теперь быть с плоскостью? ОТВЕТ: не с плоскостью, а с проективной плоскостью. Она получается из обычной плоскости «подклеиванием» к ней «бесконечно удален­ной прямой», составленной из различных бесконечно удаленных точек. Так она, наверное, бесконечная? Нет, не бесконечная. Но очень необычная. Гуляя по проективной плоскости, можно совер­шенно незаметно перейти с одной стороны плоскости на другую. Точнее говоря, на ней НЕТ «одной» и «другой стороны» – сторона у нее только одна. Подумайте над этим! Допустим, гуляли по этой плоскости два совершенно одинаковых близнеца: Alexey Savvateev и Алексей Савватеев. Кто‑ то из них остался стоять на месте, а дру­гой тем временем быстро пробежался по проективной плоскости и оказался с другой стороны – как раз под первым из близнецов. Представляете, как они жестоко поспорили – кто из них стоит нормально, а кто – вниз головой? ПОДСКАЗКА. Раз они живут на этой плоскости, то их рост (как и толщина проективной плос­кости) равен 0 см.

Насчет проективного пространства. Вы уже догадались, что для его получения надо к обычному пространству «подклеить» бесконечно удаленную плоскость, состоящую из бесконечно уда­ленных точек. Во всех случаях при проективном преобразовании вновь добавленные точки могут спокойно переходить в старые точ­ки, и наоборот. Они никак не отличаются друг от друга. Вы ска­жете: «Такого не может быть, потому что не может быть никогда! Как же можно одну перепутать с другой? Ведь прежние точки бы­ли близким к нам, а эта связана с бесконечностью, то есть очень далекая».

Так вот. В проективной геометрии НЕТ таких понятий, как «близкий» и «далекий». Ее выдумали для других целей. Так что все точки (в пределах понятий этой науки) одинаковы. Зато в ней есть свои важные понятия: прямая, плоскость, точка, двойное от­ношение и многое другое. Например, есть такое понятие, как КО­НИКА. Что это за зверь? Это не один зверь, а сразу три – в нашей обычной геометрии они назывались «эллипс», «гипербола» и «па­рабола». А в этой геометрии они НЕРАЗЛИЧИМЫ.

И в заключение полезно сообщить важную информацию и важ­ную теорему.

Информация. При проективном отображении одной проектив­ной плоскости на другую проективную плоскость любые три точ­ки, лежавшие на одной прямой, превратятся в три точки, ТОЖЕ лежащие на одной прямой.

Теорем, а. Для любых двух четверок точек А, В. С. Г) и М, N, Р, Q (в каждой из четверок любые три точки не лежат на одной прямой) существует ровно одно проективное преобразование /, для которого f(A) = М, f(B) = N, f(C ) = Р, /(Ј) = Q.

А теперь как НАДО было решать эту задачу (построить каса­тельную из точки к окружности одной линейкой, см. рис. 121).

Прежде всего, мы выходим из плоскости в пространство. Выби­раем там еще одну плоскость. Я проецирую на нее мою картинку (рис. 123) из некоторой точки А. Причем точка А и новая плос­кость расположены так, что прямая АО и эта плоскость парал­лельны. (О – это точка, в которой пересекаются три произвольно проведенные мною прямые, а также касательная, пока еще мною не построенная. )

 

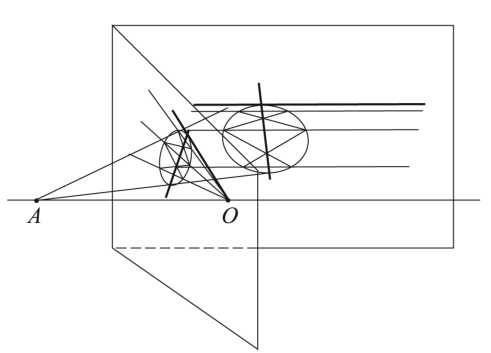
Рис. 123. Исходная картинка с гипотетическим построением касательной расположена в «левой» плоскости. Точка пересечения всех прямых на ней обозначена за «О». Точка А еще левее. Прямая АО параллельна правой плоскости, и в ней мы видим ту самую картинку, которая всё и объясняет.

Моя точка О  уйдет па бесконечность, так как ей не найдется места на новой плоскости (для того мы и брали прямую АО парал­лельной новой плоскости), окружность превратится в эллине, а все прямые, проходившие через точку О в параллельные прямые. Их точка пересечения ушла на бесконечность, прямые не пересе­каются. а значит, в геометрии Евклида они параллельны. (Мне. конечно, не могли дать эту задачу на школьном экзамене в рам­ках неевклидовой геометрии. )

А теперь смотрите, как все просто. Наша окружность с прямы­ми перешла в следующую конструкцию (рис. 124). На ней пучок параллельных прямых сечет эллине. Требуется построить прямую того же пучка, касательную к эллипсу. Очевидно (и подробно об­основано в пояснении к рисунку), что построение, аналогичное сде­ланному мной, решает данную задачу.

Но свойство касания сохраняется при проектировании: раз пря­мая с эллипсом имеет одну точку пересечения, значит, на прообра­зе (то есть, на исходной плоскости) тоже должна быть одна общая

 

Рис. 124‑ На новой плоскости картина проясняется. Все пять прямых (здесь я провел обе касательные) теперь пересекаются в бесконечно уда­ленной точке (то есть, по‑ школыюму. не пересекаются). Окружность пре­вратилась в эллипс (а могла бы превратиться и в параболу; но нам этого не нужно). Точки касания находятся в самой верхней и в самой ниж­ней точке эллипса. «Кресты» на этом рисунке стали симметричными, поэтому ясно, что их центральные точки, а также точки касания лежат на одной прямой. Значит, и прообразы этих точек лежали на одной пря­мой. Это и есть обоснование того метода решения, который я использовал в этой задаче.

точка. Следовательно, это точка касания. Теорема доказана.

Надо только выйти в пространство. Проектируете, превращаете в параллельный ноток, и всё очевидно.

Почему же я не придумал в школе такое простое решение? Дело в том. что в 11 классе, в котором изучались проективные преобра­зования (а это проективное преобразование), наша учительница литературы Зоя Александровна Блюмина решила набрать гумани­тарный класс. Чем отличается гуманитарный класс от математи­ческого класса? Конечно же. количеством девушек. Понятно, что вся математика для 11 класса была отменена явочным порядком! Все бегали к гуманитарному классу, поболтать. Я всю проектив­ную геометрию прогулял.

* *

Давайте немножко разбавим проективную геометрию. В мате­матике есть некоторое количество неожиданно прикольных задач! Они просто падают с неба. Я помню одну задачу, которую мне да­ли на олимпиаде в 7 классе. Задача про ученика, который сбежал с урока и плавает в круглом бассейне. Учитель его обнаружил в бассейне, подходит к границе бассейна с розгами в руках и гово­рит: «Я тебе сейчас всыплю. Сейчас ты только выйдешь из бассей­на, и я тебе всыплю». А ученик отвечает: «Нет, Вы же не умеете по земле бегать быстрее меня. По земле я от Вас убегу». «Ко­нечно, ты от меня убежишь, но ты же где‑ то должен высадиться из воды на землю, правильно? Вот там‑ то я тебя и схвачу за ши­ворот и выпорю розгами». «Ну да, если Вы сможете меня пе­рехватить в момент, когда я буду вылезать из бассейна, то да. Я вылезу в таком месте, где Вас не будет». «Нет, ничего у тебя не выйдет». «Нет, выйдет».

Условия задачи следующие: по земле быстрее бегает ученик; а пока он в воде, его скорость V в четыре раза меньше скорости бега учителя W, т. е. V =

Вопрос. Кто победит? Строгое решение, которое я придумал на олимпиаде, состоит в следующем. Нам дано, что скорость уче­ника в воде в четыре раза меньше скорости учителя на берегу. Давайте нарисуем окружность в четыре раза меньшего радиуса, чем бассейн. Ученик по этой окружности плывет ровно с такой же угловой скоростью, с которой учитель бегает по берегу (рис. 125).

 

Рис. 125. Учитель пыхтит, учопик плывет не торопясь.

Если я еще чуть‑ чуть уменьшу окружность, угловая скорость ученика будет больше угловой скорости учителя. Тогда через не­которое время можно добиться того, что учитель и ученик будут на противоположных сторонах (рис. 126).

 

Рис. 126. Вот так и спасся ученик. А если бы бассейн был квадратный?

В этот‑ то момент ученик и рванет к берегу. Ему надо про‑ ·1

плыть радиуса, а учителю пробежать тх радиусов (так как это

как раз длина полуокружности). Затраченное на это время равно

О 75 0 75

–^7‑ = 4 · для ученика и – для учителя. Но 4 · 0. 75 = 3 тх. Значит, ученик спасется.

Как. кстати, можно доказать, что 7г 3? Если я докажу, зна­чит. ученик сможет убежать. Что такое «пи»? Это длина половины окружности единичного радиуса. Как можно эту длину пощупать?

Был такой древний грек Евклид. Он сформулировал несколь­ко принципов работы с геометрией пять постулатов (то есть правил, справедливость которых очевидна). Вот четыре из них: 1) между двумя любыми точками можно провести прямую. 2) лю­бую прямую можно неограниченно продолжать в любую сторону.

из любой точки любым радиусом можно нарисовать окружность.

все прямые углы равны. В формулировке употребляется слово «равенство». Несмотря на то. что оно так просто звучит, это чрезвычайно сложная математическая концепция.

Первые двадцать восемь теорем книги Евклида «Начала» бы­ли сформулированы и доказаны только с использованием четы­рех постулатов. Он чувствовал, что с пятым постулатом что‑ то не так. Сейчас я его сформулирую: через любую точку, не лежа­щую на данной прямой, можно провести, прямую, параллельную данной, и только одну. То есть прямую, которая не будет пересе­кать данную. У этого постулата длиннющая интереснейшая исто­рия.

Вернемся к числу тт. Окружность это кривая, соединяющая две точки. Так вот. но одной из аксиом Евклида, отрезок прямой, который соединяет две точки, короче любой кривой, их соединяю­щей. Рассмотрим вписанный шестиугольник. Каждая сторона пра­вильного шестиугольника равна радиусу, то есть 1 (рис. 127).

 

Рис. 127. Почему 7г больше трех.

Он дает нижнюю оценку для числа тт. Число тг больше суммы трех сторон шестиугольника. А это как раз три. Так что ученик точно спасется от учителя‑ нреследователя.

Чтобы точнее оценить значение 7Г. достаточно привести в при­мер какой‑ нибудь правильный вписанный многоугольник, у кото­рого сумма половины сторон еще больше, например, правильный 8‑ угольник. Сейчас мы найдем сумму его 4 сторон. Тогда само чи­сло 7г должно быть еще больше полученного значения.

Правильный 8‑ угольник, вписанный в круг радиуса 1. может быть разбит на 8 одинаковых равнобедренных треугольников с еди­ничными боковыми сторонами и с углом 45° между ними. Отсюда легко подсчитать (с номощыо так называемой «теоремы косину­сов») что сторона этого 8‑ угольника имеет длину \/2 – \/2‑ Значит, сумма четырех его сторон равна и 3. 0615. Следовательно, точное значение 7г превосходит 3. 0615.

А для того, чтобы оценивать число тг всё точнее и точнее, нужно «увеличивать число сторон до бесконечности».

Рассмотрим еще один пример бесконечности. Будем суммиро­вать числа, обратные к квадратам натуральных чисел:

1 + 1+1 +J_ + J_ +

9 16 25

Эта сумма коночная но величине, но бесконечная но количеству

слагаемых. (В отличие от суммы 1+2 + ^ + у + ‑ ‑ ‑. которая неогра­ниченно возрастает но величине но мере увеличения количества слагаемых. ) В принципе, оба утверждения совершенно неочевид­ны, так как мы не знаем, каким правилам подчиняются суммы с неограниченным количеством слагаемых. Сейчас я докажу, что сумма обратных квадратов натуральных чисел не может превы­шать числа «2».

Рассмотрим квадрат со стороной 1. Его площадь также рав‑

 

на 1. Теперь рассмотрим квадрат со стороной ^ а площадью ^

(рис. 128). Площадь следующего квадрата со стороной ‑ равна ‑.

О У

 

 

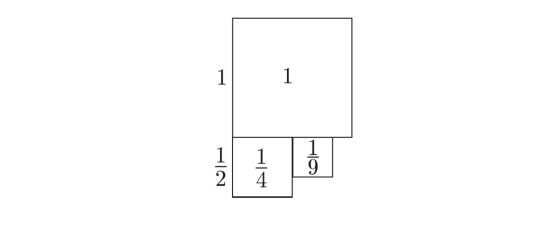
Рис. 128. Геометрический смысл исходной суммы.

Нам нужно слагаемое ‑, но я возьму с запасом. Вместо ква‑

1 драта со стороной ‑ рассмотрю квадрат со стороной к. И, значит, о L

с площадью у. Понятно, что если новая сумма будет конечной, то и исходная тоже должна быть конечной, потому что я увеличил третье слагаемое.

1111 1 Что я сделаю дальше? –г. –. тгг.. ~гг все заменю на 777. От это‑

16 ' 25 ' 36 ' 49 16

го сумма опять увеличится. А что такое одна шестнадцатая? Это

площадь квадрата со стороной ‑. Получаем 4 квадратика, так как

мы поменяли четыре прежних слагаемых на четыре раза по (рис. 129).

 

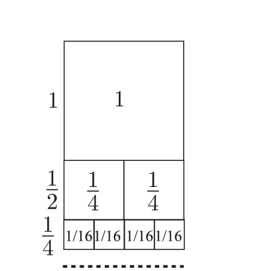
Рис. 129. Геометрический смысл увеличенной суммы. Как известно.

1+ 1 + 1+ J‑ + =1 " " '

2 4 8 16

Следующие восемь слагаемых я заменю на И они займут еще одну полосочку, вдвое меньшей ширины, чем предыдущая.

Следующие шестнадцать слагаемых еще одна полосочка и так далее. Итоговая сумма вся. целиком, будет меньше, чем пло­щадь двух изначальных квадратов. Потому что каждая следую­щая полосочка по ширине вдвое меньше предыдущей. Поэтому вся сумма не больше двух (рис. 129).

Но хотелось бы узнать, чему она на самом деле равна. Ее посчи­тал Леонард Эйлер. Один из величайших математиков в истории человечества. Он выяснил, что сумма обратных квадратов равна

7Г²

и 1. 6449. И доказал это с помощью дифференциального и ин­тегрального исчисления. Дифференциальное и интегральное исчи­сления совершают чудеса. Потому что дифференциальное и инте­гральное исчисления это способ простого перешагивания через

бесконечность. Как устроено доказательство? Примерно так: пред‑

положим, что сумма меньше Тогда она меньше на некоторую величину. Но этого быть не может: мы можем взять так много чле­нов этой суммы, что разница между ней и числом была мень­ше любого наперед заданного числа, в том числе и этой величи­ны. Про бесконечную сумму обычно показывают, что она не может быть больше какого‑ то числа по одним соображениям, и меньше по другим. На самом деле в доказательстве используются намного

более сложные соображения, связанные с математическим анали‑

7Г²

зом, которые и показывают, что эта сумма в точности равна –.

 

Другая потрясающая страница развития математики связана с пятым постулатом Евклида. Евклид сформулировал пять постулатов. Но многие теоремы он доказал, не используя пятого постулата. Из‑ за этого геометры стали думать, что пятый посту­лат на самом деле не постулат, а теорема, и он должен следовать из предыдущих четырех. С античных времен до середины XIX ве­ка ученые пытались доказать это. Сначала пытались вывести этот постулат из других, а потом пошли от противного: допустим, 5‑ й постулат НЕВЕРЕН. Что из этого будет следовать? Некоторых ученых интересовал вопрос: может быть, нам только кажется, что через данную точку можно провести только одну прямую, парал­лельную данной. А на самом деле, если рядом через эту же точку нарисовать еще одну прямую (почти неотличимую от первой), она тоже будет параллельна данной (только мы этого не можем раз­глядеть) (рис. 130).

Рис. 130. Этот пятый постулат дал им всом прикурить!

Значит, если так, то должна быть какая‑ то непротиворечивая геометрия, в которой пятый постулат будет заменен на альтерна­тивный. Например, что через данную точку можно провести как минимум две прямые, не пересекающие исходную. И вот ученые начинают пытаться привести к логическому противоречию такое предположение. И каждый из них, обнаружив какие‑ то необыч­ные следствия, говорит: ну а это уже полный абсурд. Например, пятый постулат эквивалентен утверждению, что сумма углов тре­угольника равна 180°. И, если пятый постулат неверен, то в такой геометрии не существует ни одного треугольника с суммой углов, равной 180°. Ну, это же абсурд! Значит, говорили ученые.

всё доказано. Никто не замечал, что абсурд наступает исключи­тельно из‑ за непривычности этих следствий, а не как логическое противоречие. Возьмите сферу и посмотрите, какая будет сумма углов у треугольника на сфере. Она всегда БОЛЬШЕ 180 граду­сов (нарисуйте треугольник на глобусе и убедитесь в этом! Только учтите, что «прямой» на глобусе является кратчайший путь, то есть «дуга большого круга»). Этот пример показывает, что логи­ческих противоречий в таком факте нет.

Следующий шаг работы математиков привел к эквивалентности пятого постулата и утверждения, что существует хотя бы два по­добных, но не равных друг другу треугольника. Опять же, на сфе­ре нет такого понятия, как «подобие фигур». Абсолютно нетри­виальное утверждение про поверхность нашей планеты. Нарисуем два треугольника на поверхности земного шара, или на глобусе, например, треугольник Москва – Лондон – Иркутск и треуголь­ник (Нью‑ Йорк) – (Лос‑ Анджелес) – (Рио‑ де‑ Жанейро). Если мы измерим углы у этих двух треугольников и, например, обнару­жим, что они попарно равны друг другу, то и сами треугольники окажутся равными, то есть совмещающимися движением сферы – поворотом, отражением или их композицией26. А тогда и соответ­ствующие стороны у них будут равными, то есть попарные рас­стояния между городами окажутся одинаковыми! (Разумеется в приведённоми выше примере это не так. )

Таким образом, на сфере (в частности, на поверхности Зе­мли) справедлив Признак равенства треугольников по трем углам. Это можно доказать совершенно строго. (Почему же лю­ди, – даже такие, как Евклид, – этого не замечали? Потому, что их жизненный геометрический опыт ограничивался наблюдением малых участков поверхности Земли – и они казались плоскими. ) На сфере вообще много чудес. Например, на сфере, радиус которой равен 1, площадь треугольника равна сумме углов (в радианах) минус 7г. Вот такая вот теорема. Это всё очень красивые резуль­таты сферической геометрии. То есть в «абы‑ как заданной гео­метрии» все привычные нам утверждения не обязательно верны. Была разработана целая наука, объединенными усилиями многих ученых было выведено двадцать утверждений, эквивалентных пя­тому постулату. Но никакого прямого (логического) противоречия в его отрицании не было. В начале XIX века Гауссу написал пись­мо венгерский математик Янош Бойяи. Он писал, что разработал геометрию без пятого постулата, не видит в ней никаких противо­речий и спрашивал, что ему делать. А Гаусс ответил, что знает, что там нет противоречий, но сказать этого вслух нельзя, потому что «мы разворошим осиный улей, и нас искусают осы». Однако великий русский математик Николай Иванович Лобачевский, рек­тор Казанского университета, в 1829 году написал: «Геометрия, разработанная мною, не только не противоречива, а на самом де­ле всё именно так и происходит во Вселенной». Когда Гаусс узнал, что Лобачевский не побоялся и опубликовал свои результаты, он сразу предложил выбрать Николая Ивановича в иностранные чле­ны германской академии наук и перестал скрывать свои разработ­ки в этой области. Лобачевский построил геометрию с огромным количеством теорем. В частности, одна из теорем гласила, что сум­ма углов в ЛЮБОМ треугольнике меньше 180 градусов! Он даже пытался мерить углы между звездами, чтобы доказать, что сум­ма углов треугольника хоть чуть‑ чуть, да меньше ста восьмидеся­ти градусов. В одной из современных космологий всё именно так и устроено (но для проверки этого надо делать замеры не в мас­штабах Земли, а в гораздо больших масштабах). Итак, у любого треугольника в геометрии Лобачевского сумма углов меньше 180°. И площадь треугольника равна сто восемьдесят градусов минус сумма углов. То есть сферическая геометрия как бы «выпуклая», а геометрия Лобачевского – вогнутая. Современная топология многим обязана Лобачевскому, потому что он открыл этот «ящик Пандоры». Подведем итог «поумнения» человечества в результа­та исследований 5‑ го постулата Евклида.

Возможны три типа «геометрий»: 1) геометрия Евклида (сум­ма углов любого треугольника равна 180°); 2) геометрия того ти­па, который исследовал Лобачевский (в ней через точку, взятую вне прямой, проходит МНОГО прямых, не пересекающих данную; в любом треугольнике сумма углов меньше 180°); 3) геометрия то­го типа, который исследовал Риман (через точку, взятую вне пря­мой, не проходит НИ ОДНОЙ прямой, не пересекающей данную; в любом треугольнике сумма углов больше 180°).

И все эти геометрии логически непротиворечивы!

А. С.: Сейчас мы вернемся к Евклиду. Он был не только геоме­тром, но также еще доказал замечательный фак

⇐ Предыдущая27282930313233343536Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: