Нерешенные математические проблемы

Самая старая – из известных мне – нерешенная математиче­ская проблема. Говорят, был такой в Сиракузах царь или вельмо­жа, который занимался странным видом деятельности22. Он брал натуральное число. Если оно было четное, он делил его на 2, пока оно не станет нечетным. Например, если это было число 12, оно превращалось в 3.

12 – 6 – 3.

А вот когда оно становилось нечетным, он умножал его на 3 и при­бавлял единицу. То есть 3 он превратил бы в число 10. А 10? Сна­чала в 5, потом в 16. 16 в 8, 4, 2, 1 и в итоге в 4.

12 – 6 – 3 – 10 – 5 – 16 – 8 – 4 – 2 – 1 – 4.

Как видите, мы сейчас пришли к циклу:

4 –у 2 –у 1 –у 4 –у 2 –у 1 –у 4 –у 2 –у 1...

Давайте возьмем еще какое‑ нибудь число. Скажем, 13 возьмем.

‑ Ґ 40 ‑ Ґ 20 ‑ Ґ 10 ‑ Ґ 5 ‑ Ґ 16 ‑ Ґ 8 ‑ Ґ  4 2 1 4.

Опять начинается такой же цикл. Возьмем 17.

в этой проблеме интересно? Вспомним теорему Ферма (для нее тоже получалась всё более длинная цепочка степеней «п», для ко­торых она верна). Но ее доказали для любого «п» без помощи ком­пьютера (в принципе, если бы компьютер предложил три числа ж, у, z и степень «п», которые опровергли бы теорему Ферма, он бы решил проблему). А в нашем случае компьютер ничего не может. Разве сам только он найдет какой‑ то новый цикл!

В 1994 году Уайлз, готовясь к докладу, нашел ошибку в сво­ем доказательстве «великой теоремы Ферма». К счастью, ошиб­ка оказалась несущественной и была им исправлена. А 1 апреля ему пришло электронное письмо, в котором математик, известный Уайлзу, писал, что, пользуясь его методами, он опроверг теорему Ферма. В письме приводились числа и опровержение, содержащее маленькую, незаметную ошибку... У Уайлза был шок (он забыл про 1 апреля). К счастью, эта шутка оказалась не смертельной.

Но теорему Ферма в итоге долгих усилий доказали, а рассма­триваемую нами – нет. Уже столько лет требуется человек (апре­леустойчивый), который это докажет.

Следующая по сложности проблема ‑ тоже простая (по форму­лировке, конечно). Она поставлена сравнительно недавно. И я со­вершенно уверен, что ее скоро решат.

Давайте рассмотрим прямую линию. Можно ли раскрасить пря­мую линию в две краски так, чтобы точки на расстоянии единица всегда получались разноцветными? Ясно, что одного цвета недо­статочно, а в два цвета раскрасить можно. Например, всю прямую можно разбить на полуотрезки длины 1 с отброшенным правым концом. И эти полуотрезки поочередно закрашивать то красным, то зеленым цветом.

Поэтому для прямой минимальное количество цветов, которое требуется, чтобы любые две точки на расстоянии 1 были разно­цветными, равно двум. Соответствующее число для плоскости ни­кому не известно.

Давайте рассмотрим некоторые начальные соображения. На плоскости есть равносторонний треугольник со стороной 1 (рис. 103). Закрашивая всю плоскость, мы, конечно, закрасим и всю площадь этого треугольника, и всю его границу в част­ности. закрасим и все вершины этого треугольника.

 

Сколько нам нужно цветов?

Слушатель: Хотя бы 3...

А. С.: Да, двух уже недостаточно. Иначе из трех вершин на рас­стоянии 1 друг от друга две окажутся одноцветными. Ведь этот треугольник специально взят таким, чтобы длины его сторон бы­ли «запрещенными».

Поэтому нужно хотя бы три разных цвета (скажем, К крас­ный, С синий, 3 зеленый). Представьте себе, что с трех сто­рон к этому треугольнику пририсованы такие же треугольники, затем еще и еще приклеиваем множество таких «особо трудных» треугольников, пока вся плоскость не окажется сплошь покрытой ими. (Математики в этом случае говорят так: рассмотрим на плос­кости ТРЕУГОЛЬНЫЙ ПАРКЕТ. ) Раскрасив правильным обра­зом этот паркет цветами К, С, 3 (если бы нам это удалось), мы бы полностью решили поставленную задачу для плоскости. Вы, конечно, догадываетесь, что нам не удастся этого сделать (иначе бы эту задачу давно бы уже решили опытные математики). Но мы всё же попробуем это сделать возможно, от этого расширит­ся горизонт наших знаний. Сначала раскрасим правильным обра­зом только вершины, 3‑ угольного паркета. Эти вершины образу­ют горизонтальные ряды на плоскости; в каждом ряду вершины 1

смещены на ^ ^1Ю отношению к предыдущему (и последующему)

Как вы видите, каждые три ближайшие вершины закрашены разными цветами, как и должно быть по условию. Ведь расстоя­ние между ними как раз равно 1. Обратите внимание, что третий ряд раскрасок совпадает с первым, четвертый со вторым, и т. д. до бесконечности. В данном случае (когда мы используем только три разных цвета) это не случайность легко понять, что две вер­шины «через ребро» будут одноцветными (см. рис. 104). В самом деле, если разрешенных цветов только три. то для «отраженной» вершины просто нет выбора. Однако при любой попытке продол­жить раскраску на ребра паркета (и далее на собственно плитки) нас постигнет неудача. Эта неудача не является случайной (из‑ за того или иного неверного подхода к этой задаче), а является следствием такой (уже доказанной) теоремы: Для правильного закрашивания плоскости заведомо не хватит трех красок. Доказано и полезное добавление к этой теореме: для успешного за­крашивания заведомо хватит СЕМИ разных красок. Таким обра­зом. в настоящее время известно следующее: минимальное коли­чество красок для закрашивания плоскости равно либо 4. либо 5. либо 6. либо 7.

 

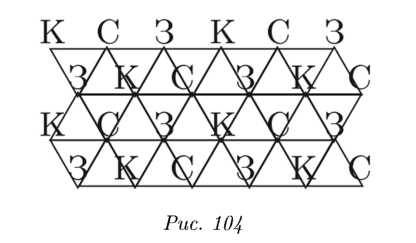
ряду. Предлагается такой способ раскраски вершин в этих рядах (рис. 104).

Эту теорему можно доказать вполне школьными вычисления­ми. и мы это сделаем жалко было бы не познакомить вас с та­ким элегантным доказательством. (Его придумали братья Мозеры. Просто взяли и предъявили 7 конкретных точек на плоскости и до­казали, что даже эти 7 точек НЕЛЬЗЯ закрасить тремя разными цветами. Значит, всю плоскость и подавно нельзя ими раскрасить. Эти семь точек образуют замысловатую конструкцию, похожую на два веретена, нижние концы которых соединены, а прочие два конца связаны веревочкой длины 1 (понятно, почему 1? ). С тех пор в жаргоне математиков появилось звучное выражение «Веретено братьев Мозеров»),

Сейчас я покажу, что на самом деле нужно хотя бы 4 цвета.

Предположим, что мы можем раскрасить плоскость в 3 цвета. Тогда любой правильный треугольник будет разноцветным (в смы­сле окраски своих вершин), а значит, у ромба из двух таких тре­угольников (рис. 105) две противоположные вершины окажутся одного цвета. Вот и получилось первое веретено!

 

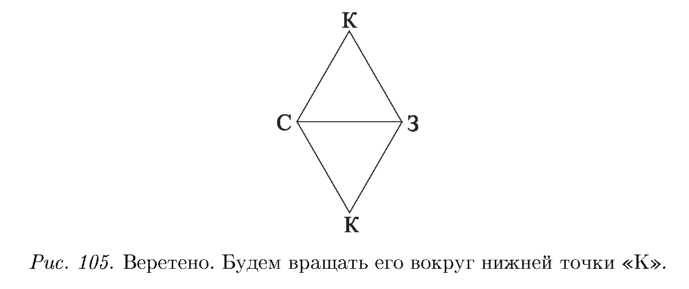
Повернем ромб вокруг одной из вершин ровно настолько, чтобы расстояние между второй вершиной и между новым положением второй вершины стало равным 1 (см. рис. 106).

На рис. 106, строго говоря, ребра нам вообще не нужны, а нуж­ны только 7 вершин. Ребра нарисованы только для лучшего пони­мания идеи доказательства. Раскрасим вершины правого веретена с номощыо цветов К, С, 3 (мы предположили от противного, что тремя цветами можно правильно раскрасить вершины «двойного веретена») (см. рис. 105). Если нижняя вершина окрашена цве­том «К», то и противоположная вершина левого веретена должна быть покрашена цветом «К». Так как горизонтальное верхнее ре‑

 

Рис. 106. Веретено братьев Мозеров. Длина всех ребер равна 1. Конструк­ция содержит 7 вершин (точки кажущегося пересечения на оси симме­трии вершинами не являются).

бро нарочно выбрано так. чтобы длина ого была равна 1. то нару­шается основное условие закраски. Теорема доказана от против­ного.

Человечество научилось красить плоскость в 7 цветов; ни в 6. ни в 5. ни в 4 оно красить плоскость не умеет и не знает, возможно ли такое.

Андрей Михайлович Райгородский. который очень любит эту проблему, считает, что возможно покрасить плоскость в 4 цвета. Но это пока никаким абсолютным доказательством, не подтвер­ждено.

 

Чтобы покрасить в 7 цветов, делается (рис. 107) 6‑ угольное за­мощение плоскости (шестиугольный паркет). Подбирается размер 6‑ угольника и предъявляется аккуратная раскраска.

С этой задачей связана еще одна проблема. Посмотрите на рис. 106 не как на схему соединения вершин «двойного веретена», а как на карту некоего 5‑ угольного острова, на котором располо­жились 9 различных государств (каждый связный кусочек, даже самый маленький, является государством). Стало быть, на геогра­фической карте этого острова каждое из государств надо было бы, по‑ хорошему, закрасить своим собственным цветом. Но государств на свете имеется ужасно много, а количество цветов, различаемое человеком, ограничено. Да и при изготовлении карты полиграфи­сты хотели бы иметь сильно ограниченный набор цветов (резко отличающихся друг от друга). Возникает чисто математический вопрос («проблема четырех красок»):

Можно ли любую карту на плоскости раскрасить в 4 цвета так, чтобы страны, имеющие общую границу ненулевой длины, были разных цветов? Или нужно 5 цветов? (То, что 3 цветов мало, до­вольно быстро показывается на примере. )

Вопрос: можно ли карту 5‑ угольного острова раскрасить 2; 3;

цветами? (см. рис. 106).

Проблема четырех красок решена в 1976 году. Путем длинней­шего компьютерного перебора, который увенчал длинное матема­тическое рассуждение, было доказано, что четырех цветов хватает для любой карты на плоскости. Даже математическая часть бы­ла столь сложна, что всерьез взялись за ее проверку только через

лет. Несколько «дырок» нашли, но все они были успешно «за­латаны».

Чтобы застраховаться от ошибки в компьютерной части, напи­сали две полностью независимые программы – ни о какой ручной проверке речи быть уже не могло. Наконец, в 1990‑ х годах первая часть тоже была автоматизирована, а в 2000‑ х всё доказательство целиком было записано на формальном языке и верифицировано программой Coq (представьте себе, есть такая программа, которая верифицирует формальные доказательства! ).

Следующий набор проблем связан с простыми числами и с де­лимостью.

Что такое простое число? Простое число – это такое целое по­ложительное число, которое делится только на два числа: на себя и на единицу. Простые числа: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, ...

Еще Евклид знал, что простых чисел бесконечное количество. Но, тут есть одно «но». Заметили, что простые числа любят по­являться парочками через один. Например, 11 и 13, или 41 и 43. Такие числа назвали «близнецами». (Числа 2 и 3 «близнецами» не называют, потому что это единственный случай, когда рассто­яние между соседними простыми числами равно единице – кста­ти, почему? ) Нерешенная проблема заключается в том, что никто не знает, бесконечно ли множество простых «близнецов».

Если мы перебираем подряд простые числа, то то и дело встре­чаем пары близнецов. Так вот, никто не может доказать, что какая‑ то конкретная пара «близнецов» последняя, или что таких пар бесконечное количество.

С удалением от нуля простые числа встречаются всё реже и ре­же. В конце XIX века Адамар и Валле‑ Пуссен доказали закон рас­пределения простых чисел. Согласно этому закону, у произвольно­го числа от 1 до п в районе большого натурального числа п шанс

оказаться простым равен.

In п

Функция «логарифм» постепенно растет, поэтому данная дробь постепенно убывает, стремясь к 0, то есть вероятность встретить простое число падает вплоть до нуля.

ПРИМЕР. Пусть п = 20. Тогда шанс встретить простое число

среди первых 20 натуральных чисел равен |––, что примерно рав­но 2" ~990 ⁼ 0, 3338. Значит, ожидается, что среди первых 20 чисел простых будет 20 · 0, 3338 = 6, 676. На самом деле их ровно 8.

А вот простые «близнецы» встречаются не регулярно – более нерегулярно, чем сами простые числа. Разрыв между ними то ма­ленький, то большой. Вопрос: стремится ли к нулю минимальный разрыв? В 2013 году было доказано, что нет.

Следующая проблема. Если вы перебираете четные числа, то их можно разбить на два слагаемых: 6 = 3 + 3, 8 = 3 + 5, 10 = 3 + 7. Всегда получается представить четное число в виде суммы двух простых:

22 = 11 + 11, 36 = 19 + 17, 66 = «на, питпите сами, какие», и так далее.

Пока все четные числа, которые смог проверить компьютер, удалось разложить в сумму двух простых. Гипотеза И. М. Вино­градова состоит в том, что любое четное число можно представить в виде суммы двух простых чисел. Виноградов доказал, что любое нечетное число можно представить в виде суммы 3 простых чисел. А вот про четные пока не могут доказать.

Совершенные числа

Сколько совершеннолетий в жизни человека? Многие думают, что одно – 18‑ летие. На самом деле совершеннолетий в жизни человека – два! Это «6‑ летие» и «28‑ летие». Потому что числа эти – «совершенные».

Что же такое совершенное число? Совершенное число – это число, которое равно сумме своих делителей, меньших, чем само это число. Какие делители у числа 6, считая единицу, но не считая его самого? 1...

Подсказка из аудитории: 1, 2, 3.

А. С.: Мы видим, что 1 + 2 + 3 = 6. Какие делители у числа 28?

2, 4, 7, 14. Всё. И снова выполняется равенство такого же типа:

+ 2 + 4 + 7+14 = 28.

В жизни человека ровно два совершенных возраста, потому что следующее совершенное число равно 496.

У математиков есть тост на совершеннолетие. Они, правда, празднуют 28, а не 18 лет. Тост всегда такой: «Чтоб тебе до­жить до следующего совершеннолетия». Но вроде как никому еще не удавалось.

Так, а в чём же загадка? Априори совершенными числами могут быть как четные числа, так и нечетные. Более того, все четные уже описаны.

Над этим потрудились Евклид и Эйлер. Первый обратил внима­ние на следующую изящную формулу: 2^{р‑ 1}(2^р – 1) (произносится она весьма своеобразно: «два в степени (пэ минус один) умно­жить на [(два в степени пэ) минус один]»). Буква «пэ» означает некоторое простое число. Первый множитель можно раздробить на самые мелкие из возможных множители (равные двум). А вто­рой множитель хотелось бы взять таким, чтобы его вообще не­льзя было раздробить, то есть в виде простого числа. (Я думаю, Евклид рассуждал именно так. Если когда‑ нибудь повстречаюсь с ним, непременно спрошу его об этом. ) Вот и высказал Евклид такую гипотезу:

Если число (2^Р^1) простое, то число 2^{р‑ 1}(2^р^1) –совершенное.

И что вы думаете? Так оно и оказалось! А потом за дело взялся Эйлер и доказал теорему посложнее: любое четное совершенное число можно записать в таком виде. Чтобы вас немного «попу­гать», давайте проверим формулу Евклида при р = 13. Получает­ся четное число 33550336. Странные цифры, правда? Кто не верит, что это число совершенное, проверьте.

А с нечетными не всё так хорошо. Когда я учился в матклассе, у нас были листочки с задачами. И вот на одном, лист, очке была задача с тремя звездочками: «Докажите, что нечетных совершен­ных чисел не существует».

Я посидел дома денек, другой. Пришел в школу и говорю учите­лю: «Что‑ то... я не могу доказать, честно. .. » А он, мне в ответ: «А... Да, это никто не может доказать! Я на всякий случай дал. Вдруг кто‑ нибудь решит... »

Вот такая проблема! Существуют ли нечетные совершенные чи­сла? Компьютеры пока перебирают варианты. Если компьютер найдет, то проблему снимут. А если не найдет, то надо доказывать, что их не существует. В конце этой темы я хочу задать задачу‑ шутку (а решение – не шутка): бывают ли совершенные числа, которые в десятичной системе записываются одними семерками?

Напоследок две решенные недавно задачи.

Возьмем много‑ много одинаковых шаров. Начнем приставлять их друг к другу с разных сторон (в пространстве).

Сколько одинаковых шаров можно приставить вплотную к од­ному шару такого же размера? Она называется задачей Ньюто­на. Ньютон очень долго переписывался с Д. Грегори. Ньютон был уверен, что можно приставить только 12 шаров, а Грего­ри утверждал, что 13. В результате доказали, что 13‑ й шар чуть‑ чуть не влезает. Ну, разумеется, возникает естественный вопрос, а в 4‑ мерном пространстве сколько шаров влезет? Задача решена в 2013 году нашим соотечественником О. Мусиным. Он еще жив и вполне себе в рабочем настроении. То есть в 4‑ мерном простран­стве она решена, а в 5‑ мерном, кажется, еще нет.

А теперь, наконец, Гипотеза Пуанкаре.

Что мы знаем о нашем мире? Во‑ первых, что он 3‑ мерный. Во‑ вторых, у него нет края. Края в том смысле, в котором его воспри­нимает таракан, подползая к краю стола. Мир везде одинаковый. То есть таракан ползет по сфере или по бесконечной плоскости. А люди «ползают» по трехмерной сфере или по бесконечному про­странству (а где именно – надо бы уточнить).

А еще наш мир ориентированный. То есть что бы вы ни делали в этом 3‑ мерном мире, ваша правая нога никогда не станет левой.

Исследования в области теоретической физики (так называе­мые уравнения космологии Фридмана и других ученых) не исклю­чают того, что наш мир конечен. Можно даже представить себе, что сверхдалекие звезды, которые видны справа и слева от Зе­мли – это одни и те же звезды. И, может быть, мы сможем увидеть на небе Землю, улетая от нее вертикально вверх, долго‑ долго летя и возвращаясь на эту же Землю с другой ее стороны! Это трудно себе представить, но такая гипотеза не противоречит современным научным данным.

Наше пространство, возможно, является искривленным, то есть служит примером нетривиального трехмерного многообразия. Мо­жет ли к нему быть применена гипотеза Пуанкаре, доказанная Пе­рельманом? Вернемся к «двумерным мирам». Если я беру камеру от колеса (рис. 108), продеваю в него нитку и завязываю, то я ни­когда не смогу ее снять. А если я завяжу нитку на сфере, я сниму ее без проблем. Всё, что нам осталось предположить про наш мир, чтобы применить к нему гипотезу Пуанкаре, это принять на веру, что в нашей вселенной «трюк с завязыванием петли» не пройдет, и любую петлю можно стянуть. Описанное свойство поверхности сферы, но не камеры! носит название односвязности23.

 

Рис. 108. Пусть наш Космос имеет форму «бублика», только не дву­мерного. а трехмерного, расположенного в пространстве более высокой размерности. Как бы могли подтвердить этот факт земные космонавты? По наличию «дыры» в этом бублике.

 

Так вот, если наш трехмерный мир конечен и односвязен, то мм попадаем в условия теоремы, Пуанкаре Перельмана. И тогда он обязательно является 3‑ мерной сферической поверхностью 4­мерного пространства‑ шара.

Обычная сфера радиуса 1 задается уравнением: х ²  + у ²  + z ²  = 1.

А 3‑ мерная того же радиуса вот так: х ²  + у ²  + г² + к ²  = 1. (По­думайте, почему координат на единицу больше, чем размерность! )

Раньше это была гипотеза Пуанкаре и относилась она только к топологии. Теперь это теорема Пуанкаре Перельмана. И теперь ее можно пытаться применять в космологии.

Раздел II

«Знание геометрии артиллеристу и инженеру необходимо, а каждому, кто только чему‑ нибудь учиться хочет, нужно; сия наука есть истинное основание всем наукам в свете, она научает нас здраво разсуждать, вер­но заключать и неопровергаемо доказывать; она сохраняет нас от многих заблуждениев, ибо геометристу труднее какое‑ нибудь предложение дока­зать обманчивыми доводами, нежели философу.

Эвклидовы элементы суть основании сей несравненной науки – не­обходимо учащимся предлагать должно, и стараться, чтоб они их знали совершенно... »

 

Всеподданейший доклад генерал‑ фельдцейхмейстера графа П. И. Шу­валова об учреждении при артиллерии шляхетного кадетского корпуса с классом военной науки (1757 г. )

 

⇐ Предыдущая24252627282930313233Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: