 |
Кп‑1 кп‑2 кп‑3
|
|
|
|
Лекция 1
А. С.: Сейчас мы рассмотрим несколько сюжетов. Некоторые мы разберем сразу, а некоторые оставим и потом к ним вернем‑
Первый сюжет называется фотосъемка.

Давайте представим себе такую ситуацию: на прямой дороге расположено несколько контрольных пунктов (КП). Над этим отрезком дороги непрерывно идет аэрофотосъемка (рис. 109).
‑ о–о о–
КП‑ 1 КП‑ 2 КП‑ 3
Рис. 109. Участок усиленного наблюдения.
И вот однажды сверху засекли шпиона (рис. 110).
объект
‑ о–о–·–о–
КП‑ 1 КП‑ 2 КП‑ 3
Рис. 110. «Возле самой границы овраг. Может, в чаще скрывается враг! »
Требуется понять, где конкретно он находится на дороге. Из визуальных соображений ясно, между какими двумя КП находится шпион, но нам нужна точная координата. Мы видим только фотоснимок. Мы можем запросить некоторое количество информации. например, мы можем запросить координаты некоторых КП. Вопрос: сколько координат нам для этого достаточно запросить. Задача вполне практическая. Фотосъемка достаточно сложное преобразование, относящееся к проективным.
Что это такое? Давайте немного разберемся (см. рис. 111).
При фотографировании происходит перенос каждой точки местности вдоль лучей по направлению к точке съемки. Прямая, конечно. переходит в прямую при таком проецировании. Но вот соотношения отрезков‑ расстояний становятся другими.
Ясно, что одной координаты для опеределения местоположения недостаточно. Фокус в том. что двух координат тоже недостаточно.
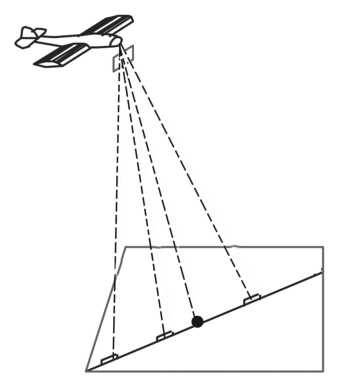
Рис. 111. Схема аэрофотосъемки. Два четырехугольника это область, снимаемая на фотопленку (внизу), и границы кадра фотопленки (вверху). Эти две плоскости, как правило, не параллельны друг другу. Из‑ за этого искажаются соотношения расстояний между точечными объектами. Прямая внизу охраняемая дорога, на которой расположены три КП (достаточно далеко друг от друга). Черный кружок указывает на место обнаружения подозрительного точечного объекта. Пунктирные линии изображают отраженные лучи света, исходящие от точечных объектов на дороге и фиксируемые на кадре пленки.
|
|
|
А вот три координаты в самый раз. Потому что у этого преобразования у проецирования есть то. что математики называют «инвариант».
Если вкратце сказать, «о чём» математика, то она о том. чтобы выявлять инвариантность ситуации. То есть какие‑ то соотношения. которые остаются неизменными. Вот вы так измерили (расстояния между КП). так сфотографировали, этак сфотографировали некоторое соотношение координат точек на всех снимках будет одно и тоже. Я сейчас просто напишу, что остается неизменным. На самом деле это можно строго доказать.
На всех фотографиях, для любых фотоаппаратов неизменным остается так называемое двойное отношение «ДвОт» четырех точек (три из них координаты КП, четвертая координата подозреваемого в шпионаже). Оно выражается формулой

„ (z – х) (t – х)
ДвОт = ) (: )‑ ( (см. рис. 112). (5)
{z ‑ у) (* ‑ у)
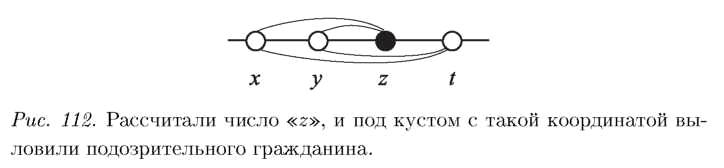
Если но знаешь, ни за что но угадаешь! Это число, которое можно взять и посчитать. Оно будет одинаковым и для местности, и для фотографии. Поэтому я запрошу координаты трех КП, потом вычислю соотношение на фотографии (на которой отражены и положения КП, и расположение неизвестного объекта), приравняю его к выражению с реальными координатами и точно определю реальную координату искомого объекта (а именно, число z).
|
|
|


