ело i – НЕ вещественное. Противоречие. Значит, х + yi и z + ti равны тогда и только тогда, когда х = z и t = у одновремен­но.

% =.

 

t^y

х   – Z  

Этого не может, быть, так как ‑ т вещественное число. А чи‑

 

ело i – НЕ вещественное. Противоречие. Значит, х + yi и z + ti равны тогда и только тогда, когда х = z и t = у одновремен­но.

Из этого следует, что каждой точке плоскости соответствует единственное комплексное число.

Продолжение в следующей лекции (то есть в лекции 4 части 2).

Лекция 4

А. С.: Сегодня мы будем заниматься комплексными числами. Но для начала интересная зарисовка из теории вероятностей. Если бы нас было человек 30, я бы поставил 5 мороженых к 1, что у дво­их из здесь присутствующих совпадут дни рождения. На самом де­ле граница проходит на числе 23. Если в аудитории 23 человека, то вероятность совпадения хотя бы двух дней рождения примерно равна 50%. Правда, совпадут только месяц и число рождения, но не обязательно год. Для людей, которые об этом не задумывались, это совершенно удивительный факт. Вроде бы всего 23 человека, как же такое может быть? Но математика открывает этот секрет.

Еще один интересный сюжет: два человека решили встретиться в метро на станции Кропоткинская. Но вышло так, что они не дого­ворились о времени. Известно лишь, что они свободны между 9 и 10 утра. Стратегия у них такая: человек приходит и ждет 15 минут. Если не дождался, уходит. Вопрос: что вероятней, встретиться или разминуться? Чему равна вероятность того, что они встретятся?

«Математическая» теория вероятностей на эту тему говорит следующее. Давайте расположим на плоскости все возможные ис­ходы в этой «игре».

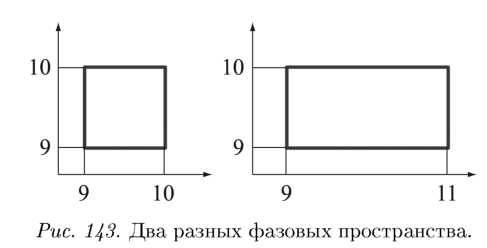
По оси х будем откладывать момент прихода первого, а по у – второго (в минутах после 9 часов). Получившийся квадрат назы­вается фазовым пространством задачи (рис. 143). А вот если пер­вый может появиться в любой момент от 9 до, например, 11 часов, то фазовое пространство будет не квадратом, а прямоугольником. Так как и момент появления первого, и момент появления вто­рого совершенно непредсказуемы в рамках промежутка с 9 до 10, следует представлять себе, что и квадрат (слева), и прямоуголь­ник (справа) покрыты равномерной сетью из большого количества точек.

Теория вероятностей постоянно оперирует с понятием «зависи­мости» и «независимости» нескольких случайных величин. Здра­вый смысл подсказывает, что наши события (то есть приход 1‑ го и приход 2‑ го) независимы. Тогда все исходы, т. е. пары (время

 

прихода первого и время прихода второго) равновероятны. Мы сейчас нарисуем зону, в которой друзья встретились, и посмотрим, какая у нее площадь (для левой части рис. 143).

Если они пришли в один и тот же момент, то из таких точек мы получим диагональ одинаковый момент прихода. Ясно, что они встретятся (и время ожидания будет равно 0).

А если они немножко отклонились от диагонали влево/вправо? Тогда тоже встретятся, потому что один из них пришел немножко раньше другого и дождался второго. Надо понять, на какое са­мое большое число минут им можно отклониться друг от друга по времени прихода, чтобы встреча еще произошла? На 15 минут. На одну четверть часа. Иначе будет как в известной песне*.

Мы получили границы зоны встречи. Что происходит на гра­нице? Первый пришел, например, в 9 часов 50 минут, а второй в 9: 35. Тогда второй, который пришел в 9: 35. уже собирался ухо­дить. и тут появился первый.

площадь оставшейся части. S = Г² = 1 площадь всего ква­* Договорились мы па завтра: «На том же место, в тот же час! »

Теперь надо посчитать площадь «встречи» (то есть участка ква­драта. описывающего пары моментов прихода, при которых встре­ча произойдет) и поделить ее на общую площадь фазового про­странства. Вычислим сначала площадь оставшейся части для слу­чая квадрата (рис. 144).

 

 

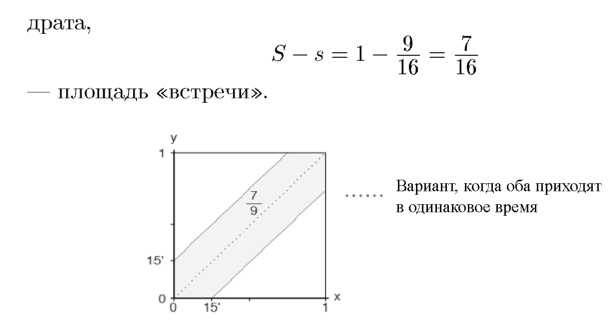
Рис. 144 · Встреча возможна только внутри шестиугольника (15' = 0. 25 часа).

7 1

Число jg чуть‑ чуть меньше То есть ждут всего 15 минут.

а вероятность встречи близка к 50%.

Упражнение. А какой будет ответ, если фазовое пространство не квадратное, а прямоугольное (рис. 143. справа)?

Про теорию вероятностей можно говорить очень долго. Это от­дельная. очень большая, интересная наука и для школьной про­граммы. и для людей, занимающихся другими науками. В теории вероятностей есть свои проблемы. Например, данные про боль­шой город типа Москвы входят в очень резкий контраст с базо­выми предположениями теории вероятностей. Рассмотрим состоя­ние пробок на дорогах. Оно складывается из миллиона случайных решений отдельных людей. Каждый, у кого есть машина, решает, поехать ли на машине или на общественном транспорте, то есть примерно миллион человек одновременно решают задачу, на чем им ехать. И типовое предположение теории вероятностей о том. что выборы людей независимы друг от друга, предсказывает абсолют­но одинаковые пробки при одинаковых метеорологических услови­ях. Если наша теория верна, если решения независимые, то долж­ны быть идентичные дорожные ситуации при одинаковых услови­ях. Аварии учесть трудно. Но одна, две мелких аварии не сильно

влияют на трафик. Математики очень мало знают про транспорт. Но самое главное – есть стойкое ощущение, что эта модель невер­на. Люди друг с другом каким‑ то образом связаны. Они реагируют на фазы Луны, пятна на Солнце или на что‑ то еще и принимают одинаковые решения. (Например, если их просят назвать извест­ного русского поэта, все как один говорят: Пушкин. ) Это – един­ственное объяснение, почему при абсолютно идентичных условиях бывают диаметрально противоположные по структуре пробки. Се­годня город едет, а завтра – стоит.

Надо признать, что нам не всё известно. Я, на самом деле, счи­таю, что про социальные науки (социологию, политологию, эконо­мику) нам вообще почти ничего неизвестно. Математики врут, ко­гда говорят, что они разобрались в том, как функционирует соци­ум. Модели примитивные, никогда ничего не предсказывают. Ино­гда объясняют то, что было вчера.

С географией дела обстоят лучше. Расселение меняется медлен­но. Редко бывает так: с утра не с той ноги встал и с досады ока­зался не в Москве, а в Иркутске31. Эталоном науки должна быть физика – наука о неживой природе. Она разработана до такой степени, которая никаким инопланетянам, наверное, не снилась. И если с физикой сравнивать науки о социуме, то математиче­ский блок социальных наук практически не развит. Поэтому вся­ким «гуру», которые появляются на «Полит. ру», в «Ведомостях» или прочих изданиях, вообще верить нельзя (в том числе и мне са­мому! ). Они делают прогнозы, а через неделю уже всё по‑ другому. Я вижу, о каких моделях они говорят, и понимаю, что там обман в каждом слове. А в математике, в лингвистике, в других не соци­альных науках нет места подвоху.

* * *

Вернемся к комплексным числам. Я хотел рассказать о том, как чудесным образом с помощью комплексных чисел решаются неко­торые уравнения. На прошлой лекции мы решили, что хотим иметь такое невещественное число г, что г ¹  = – 1. И каждой точке плос­кости сопоставили некоторое комплексное число: (ж, у) –ж + уг. Оказывается, эти числа подчиняются привычным математическим действиям: плюс, минус, умножить, разделить. Математики до­вольно большую часть времени живут в системах, которые на­зываются полями. Поле – это такое обобщение обычных чисел. Это такие системы «чисел», в которых можно совершать операции плюс, минус, умножить и разделить по нормальным обычным правилам. То есть вы пишете какое‑ то алгебраическое выражение, раскрываете скобки, делите, сокращаете. Всё, что можно сделать с обычными действительными числами, можно сделать и с элемен­тами любого поля. А поля бывают очень разные и иногда совер­шенно неожиданно выглядят32.

Мы хотим, чтобы множество комплексных чисел стало полем, то есть чтобы в нём можно было делать всё, что мы привыкли де­лать с действительными числами, в частности, умножать и делить. И об этом мы сейчас поговорим.

Было доказано, что х + уг = z + U только в том случае, если имеют место равенства х = z и у = t.

То есть если это просто одна и та же точка на плоскости. А раз­ные точки дают разные комплексные числа, поэтому комплекс­ные числа занимают как минимум всю плоскость. А из стремле­ния к минимализму мы постараемся ограничиться только точка­ми плоскости. Давайте учиться складывать, вычитать, умножать и делить точки плоскости.

Чему будет равна сумма (ж + уг) + {z + Ы)?

Мы должны получить какое‑ то комплексное число. Значит, у нас будет часть с г и часть без г. Если отложить часть «без г» по оси абсцисс, а часть «с г» – по оси ординат, то у нас по­лучится какая‑ то точка на плоскости. Часто комплексное число отождествляют с вектором (т. е. стрелочкой), ведущим из начала координат в эту точку. Из правила сложения векторов получается, что (ж + уг) + (z + ti) = (ж + z) + г{у + t).

 

Рис. 145. Сложение комплексных чисел.

Точки (х, у) и (г, t) задают нам два вектора на плоскости, выхо­дящие из начала координат. Если сложить два вектора, получится вектор с координатами (х + z, y + t).

В школе это называют правилом параллелограмма.

 

⇐ Предыдущая30313233343536373839Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: