(ci I)2 = ci 2  2а 1

(a, b, а + 1)

Теперь мы хотим, чтобы 2а + 1 было равно этому нашему числу 5². то есть 25.

2а + 1 = 25, а = 12.

Итак, мы получили новую тройку: 12² + 5² = 13². Без сомнения, ведь 144 + 25 = 169.

Следующий нечетный квадрат 49. Появится решение 24, 7 и 25.

Кто‑ нибудь из вас спросит меня: «Может быть, это всё? » Мы получили бесконечный ряд решений уравнения а ²  + Ь² = с² в целых

числах. Но они все устроены одинаково. Гипотенуза отличается от большего катета на 1.

Вопрос: а есть какие‑ нибудь другие решения? Ответ: да. Очень много других серий. Вот вам одно из решений, устроенных иначе: 84, 187, 205.

Общая формула для всех решений – это отдельная история.

Лекция 3

А. С.: Сейчас мы немного вернемся к теореме Ферма и Диофан­ту с его тринадцатью томами. Шесть сохранившихся томов, как я уже рассказывал, были изданы, после чего попали в руки Ферма. Ферма читал труд Диофанта и оставлял замечания на полях книг. Так вот, в том месте, где Диофант полностью разбирает классиче­скую задачу о прямоугольных треугольниках, рукой Ферма была на полях сделана заметка: «В то же время никак нельзя разло­жить куб в сумму двух кубов». На нашем языке это звучит так: уравнение вида ж³ + у³ = z ^{? J}  не имеет решений в целых числах.

Далее у Ферма стоит запятая, и он продолжает: «Никакую че­твертую степень – на сумму двух четвертых степеней, и вообще никакую фиксированную степень – в сумму двух таких же сте­пеней». Далее он пишет восхитительную фразу, за которой мате­матики гонялись 357 лет. Он пишет: «Я нашел тому факту пои‑ стине удивительное доказательство, но поля этой книги недоста­точно широки, чтобы его вместить». Эта запись рукой Ферма была в экземпляре трудов Диофанта. Этот комментарий был единствен­ным случаем в истории, когда утверждение Ферма не удалось до­казать за разумный период времени, спустя 20‑ 30 лет. Один раз Ферма ошибся, но он не утверждал определенно. В случае с про­стыми «числами Ферма» он написал «по‑ видимому, они простые». В случае с рассматриваемой нами теоремой Ферма написал, что на­шел доказательство. Он упомянул об этом в 1637 г., а в 1994 г. ее доказали. Мы сидели на семинаре по алгебре. Пришел преподава­тель и сказал: «У меня для вас потрясающая новость – доказана великая теорема Ферма». Все решили, что это розыгрыш, не мо­жет такого быть. Мы учимся на мехмате, и при нас происходит историческое событие. Если быть точнее, теорему доказал Эндрю Уайлз в 1993 г. Но затем в доказательстве им самим была найдена ошибка, которую Уайлз вместе с Ричардом Тейлором исправляли пол года. Поэтому окончательно теорема была доказана в 1994 го­ду. Некоторое время были сомнения, и в 1996‑ 1997 гг. не все были убеждены в том, что это свершилось, так как понять это дока­зательство могли лишь немногие из математиков. Сегодня можно утверждать, что понимают доказательство этой теоремы человек 500 в мире, детально – около 100 человек. Ежу понятно, что Фер­ма подобного доказательства выдумать не мог. Следовательно, или Ферма один раз ошибся, или мы до сих пор не знаем простого дока­зательства этой теоремы. Математики предпочитают соглашаться с первым утверждением, ибо второе позорно для всего человече­ства.

Ферма не оставил доказательства общего случая, но сохрани­лись записи изящного доказательства для частного случая, для п = 4, гласящего, что уравнение ж⁴ + у⁴ = г⁴ не имеет нетривиаль­ных решений в целых числах.

Я не буду приводить этого доказательства, хотя оно и не очень сложное. Оно использует приемы делимости, что возвращает нас к нашей первой задаче (найти все пифагоровы тройки).

Итак, теорема Ферма: уравнение х ^п   + у ^п  = z ⁿ  не имеет ре­шений в натуральных числах. Давайте посмотрим, каким может быть число п.

Это число можно разложить на множители. Есть такая теорема, называется «Основная теорема арифметики», которая утвержда­ет, что любое натуральное число можно единственным образом, с точностью до перестановки множителей, разложить в произве­дение простых чисел. Смотрим, делится ли п на 2. Делим, пока делится, получаем 2 в какой‑ то степени и оставшийся нечетный множитель. Если оставшийся множитель не простой, то мы рас­кладываем его дальше, пока не получим произведение простых чисел.

Например,

п = 2^т тп ₂  Г ‑ 17‑ 7 3808.

Почему процесс разложения на множители не может продолжать­ся до бесконечности? Каждый раз, когда мы раскладываем на мно­жители, числа становятся всё меньше и меньше. Нельзя бесконеч­но долго уменьшать натуральное число. Это аксиома Архимеда, но для человека разумного это – очевидное утверждение.

Переименуем простые множители в р. Математики любят обо­значать простые числа буквой р от английского «prime»:

 

п = 2^ШР1Р2Рз · · ·Рк·

Некоторые из множителей могут встречаться несколько раз. А мо­жет быть, у п   есть какие‑ то другие множители, которые здесь не перечислены, и в результате оно одновременно равно какому‑ то другому произведению:

 

в = 2^mpip₂p3 ■ ■ ■ Рк = · · · Чк‑

Может ли такое быть, чтобы одно и то же число раскладывалось на простые множители «существенно по‑ разному» (несуществен­ное отличие – например, 2‑ 3‑ 5 и 3‑ 5‑ 2)? Интуиция подсказывает, что нет, и интуиция права. Но доказать это аккуратно довольно сложно. Мы в это просто поверим и не будем проходить этой тер­нистой дорогой. Что же следует из единственности разложения на простые множители?

Есть два варианта. Либо у п   есть хотя бы один нечетный про­стой делитель, то есть в записи:

 

п = 2^ШР1Р2Рз · · ·Рк

хотя бы одно р – нечетное. Второй вариант состоит в том, что ни одного нечетного числа нет. Поговорим сперва о втором варианте. Что можно сказать про п   в этом случае? То, что п   является сте­пенью двойки. Если п  = 2, мы получаем задачу про Пифагоровы треугольники, которую скоро решим в этой лекции. Если п ф   2, то оно представимо в виде 4‑ к. Высшая степень двойки ‑ это либо 4, либо 8 = 4‑ 2, либо 16 = 4 · 4 и так далее. Получаем следующее уравнение:

   

X^ik+y^ik = z^4k,  

но, как известно,

 

х^4к = (х^к)\

 

(^)⁴ + (У^к)⁴ = (z^k)⁴‑

Если бы можно было решить это уравнение, то три натуральных числа х ^к , у ^к  и z ^k  образовали бы решение задачи Ферма ж⁴+у⁴ = z ⁴ .

Но Ферма доказал, что такое уравнение не имеет решений в це­лых числах, строго больших нуля.

Поэтому случай теоремы Ферма для чисел п, являющихся ка­кой‑ то степенью двойки, сводится к п = 2. В других случаях ре­шений нет.

Вспомним, какой случай мы еще не рассмотрели: п содержит нечетный простой делитель р, п ф 1 (кстати, 1 тоже является сте­пенью двойки), то есть п = рк. Тогда:

 

(х^к)^р + {y^kY = (z^kf.

Получается, что если у п есть простой нечетный делитель р, то несуществование решения уравнения Ферма с показателем п сво­дится к несуществованию решения уравнения степени р.

То есть теорема Ферма сводится к исследованию уравнения про­стой нечетной степени. И если мы знаем, что ни при каком про­стом нечетном п уравнение х ¹¹  + у ^п  = z ⁿ  не имеет решения, то оно не имеет решения и ни при каком другом п ^ 3. А теперь – история вопроса.

Про уравнение второй степени было известно уже древним ин­дусам. Уравнение третьей степени оказалось более сложным. По­чти полное решение, которое потом довели до конца, было полу­чено Леонардом Эйлером. В лекции 4 я расскажу, каким изящней­шим путем доказывается теорема несуществования для некоторо­го уравнения третьей степени (не связанного напрямую с теоремой Ферма), но сначала про пятую степень:

 

х^ъ + у^ъ = z⁵.

Неразрешимость уравнения пятой степени в целых числах была доказана в XIX веке. Потом стали увеличивать показатели и дока­зывать про седьмую, одиннадцатую, тринадцатую степени. Дошли

примерно до сотни. Особо отличились женщина‑ математик Софи Жермен, а также Куммер, потративший на теорему Ферма добрую половину своей весьма долгой жизни (1810‑ 1893).

При решении уравнения Ферма выделяют два разных случая: регулярный и специальный (нерегулярный).

Регулярный случай: ни одно из чисел ж, у, г не делится на р. Специальный случай: одна из переменных делится на р, а две дру­гие – нет. (Если две переменные делятся нар, то и третья перемен­ная обязательно делится на р. Например, если ж и у делятся на р, то в левой части р выносится за скобку, и г тоже будет делиться на р. Тогда можно сократить обе части уравнения на максималь­ную степень числа р и получить какой‑ нибудь из двух описанных случаев. )

Софи Жермен далеко продвинулась в регулярном случае. Она доказала, что уравнение регулярного типа х ^р  + у ^р  = z ^p  не имеет решения для всех таких простых р (нечетных, то есть всех, кроме р = 2), что 2р + 1 – тоже простое.

Весь XIX век длилась борьба за разные простые показатели, и методология доказательств была типовая. Выражения раскла­дывали на множители типа

 

х³ + у³ = (х + у) (ж² – ж у + у²).

Если вы не помните эту формулу из школы, можете ее проверить, раскрыв скобки. Дальше незадача: (ж² – ху + у ² ) на множители не раскладывается – по той же причине, по которой не раскла­дывается ж² + у ² . А как было бы хорошо разложить его и в одну строчку получить решение! Но это возможно только с комплекс­ными числами, а с действительными, привычными нам – это не­возможно. Все дороги, которые ведут в настоящую математику – идут через комплексные числа. Это сложно, но интересно и кра­сиво. К комплексным числам мы вернемся в конце этой лекции.

Сейчас я хочу доказать математически, что два вышеупомяну­тых выражения ж² + у ²  и ж² ‑ ху + у ²  не могут быть разложены на множители. Для этого я использую сложный, но наглядный путь через введение в алгебраическую геометрию.

Докажем неразложимость х ²  + у ² . Допустим, что его можно раз­ложить на множители (где а, /3, 7 и 5 вещественные числа):

 

х² + у² = (ах + /Зу)( jx + Sy).

Рассмотрим, какие множества на плоскости задают правая и левая части уравнения:

 

х² + у² = 0 и (ах + /Зу)(‑ ух + Sy) = 0.

После работ Декарта мы знаем, что х и у можно считать координа­тами на плоскости. Уравнение х ²  + у ²  = 0 задает нам только одну точку (0, 0). Почему? Потому, что квадраты не могут быть отрица­тельными. Если одна из переменных положительна, например х, то выражение х ²  больше нуля, но квадрат второй переменной не меньше нуля, следовательно, сумма будет больше нуля. Не по­лучается. Если сумма равна нулю, значит х и у оба равны нулю. Рассмотрим второе уравнение:

 

(ах + [Зу)( jx + Sy) = 0.

Оно задает нам две прямые. Иногда они могут совпадать.

 

х² + у² = 0 (ах + /Зу)('ух + Sy) = 0.

 

Рис. 136. Для левого уравнения получается всего одна точка, для пра­вого или две прямых, или одна.

Получается, что с одной стороны у нас две прямые (в случае их совпадения одна), а с другой стороны точка (см. рис. 136).

Если бы х ²  + у ²  раскладывалось на множители, то второе урав­нение должно было бы определять то же множество на плоскости, что и первое. Но так как эти множества не совпадают, то сумму квадратов нельзя разложить на множители.

Вот вам пример методов классической алгебраической геоме­трии. Если я захочу изучать уравнение от трех переменных ж, у и z, то получится уже трехмерное пространство. А если у меня 26 переменных? Нам понадобится 26‑ мерное пространство. Нуж­но иметь воображение и жить в многомерном пространстве. Пред­ставьте, что вы выходите на улицу и переходите дорогу на красный свет. Вас может сбить машина, но стоит вам перейти в четырехмер­ное пространство, и вам станут безразличны все светофоры, так как машины будут проезжать сквозь вас, и даже не будут заме­чать этого. А ведь вы сделали только один шаг по четвертой оси координат!

Немного сложнее доказать, что не раскладывается на множи­тели х ¹  – хлу + у². Допустим, что

 

ж² – ху + у¹ = (ах + /Зу)(ух + 6у).

Посмотрим на множество ж² – ху + у² = 0.

Умножим всё на 4, затем преобразуем:

4ж² – 4жу + 4у² = 0,

4ж² – 4жу + у² + 3 у² = 0.

Свернем 4ж² – 4жу + у² = (2ж – у)² по формуле Бинома Ньютона.

Получим (2ж – у)² + 3у² = 0.

Если сумма квадратов равна 0, значит, каждый из них равен 0. Значит, во‑ первых, 3у² = 0, то есть у = 0. А во‑ вторых, (2ж^у²) = 0, то есть 2ж – у = 0, откуда в силу у 0 имеем ж 0. То есть это уравнение задает точку (0; 0). Но (ах + /3y)(jx + 8у) по‑ прежнему задает две прямые (в крайнем случае, одну). Множества опять не совпадают. Значит, разложить ж²^жу+у² на множители нельзя.

Зачем мы это делаем? Я снова сделаю переход от истории к ма­тематике.

Вернемся к ж² + у² = z ² . Рассмотрим несколько способов реше­ния этой задачи.

Первый способ решения называют «формулой индусов», т. к. по­лагают, что еще древние индусы знали это решение.

Давайте посмотрим, какие бывают варианты для четности или нечетности ж, у и г? Если число четное, оно имеет вид 2к, тогда его квадрат имеет вид (2к) ²  = 4к ²  и он делится нацело на 4. (В не­которых книгах факт делимости изображается так: 4к ²  : 4. )

Если число нечетное, то его можно представить в виде выраже­ния 2к + 1 для некоторого целого к, и тогда

(2 к + I)² = 4fc² + 4fc + 1 = 4(fc² + к) + 1.

4(fc²+fc) + l – не просто нечетное число. Это число, которое при де­лении на 4 имеет остаток 1.

Какие бывают остатки при делении на 4? 1 и 3 у нечетных чисел и 0 и 2 у четных. Так вот, выведенные формулы показывают, что у квадратов всегда остатки либо 0, либо 1. Например,

О² = 0, I² = 1, 2² = 4,

то есть ноль при делении на 4, далее – 9, 16, 25, 36, 49 (с чередо­ванием остатков 1 и 0 при делении на 4).

Тут есть еще один более глубокий «фокус‑ покус»:

(2 к + I)² = 4 (к ²  + к) + 1 = 8^±1 + ¹ = 8^–^ + 1, к(к + 1)

где ^ всегда целое число. В числителе стоят два подряд

идущих числа. Оно из них всегда четное, значит, это выражение делится на 2.

Получается замечательная вещь. Квадрат любого нечетного чи­сла дает остаток 1 при делении на 8. Это – очень важный факт. Но в нашем случае важен остаток при делении на 4.

Вернемся к нашему уравнению

х ²  + у ²  = z ²  (7)

(так как это – формулировка теоремы Пифагора, то такие пря­моугольные треугольники со сторонами х, у, z, где х, у, z – целые числа, называются «пифагоровыми»).

Прежде всего сократим все на 2.

Делим на 2 все три числа, пока они синхронно будут делиться. Затем, заодно, разделим все три числа на все их прочие общие про­стые множители. Так мы опишем не все треугольники, а только качественно разные. Поясним сказанное, воспользовавшись поня­тием подобия треугольников.

Если два треугольника подобны, то тройки их сторон пропор­циональны друг другу. Интересно в каждом семействе подобных друг другу пифагоровых треугольников найти самый маленький треугольник с целыми сторонами. Потом мы сможем умножить найденное решение (x, y, z ) на любое целое положительное число. Треугольник увеличится, но останется пифагоровым.

У этого самого маленького треугольника не будет делимости ни на одно простое число у всех трех сторон одновременно. Но и дли­ны двух сторон не могут делиться, например, на 2, иначе длина третьей стороны тоже будет обязана делиться на 2, так как выпол­няется равенство (7). Если делятся слагаемые, то делится и сумма, значит, можно сократить все три числа.

То есть у минимальных троечек из этих трех чисел на 2 мо­жет делиться только одно. Аналогично и на любое другое простое число может делиться длина не более одной из трех сторон.

Оказывается, что не подходит тот вариант, когда х, у, z – все нечетные числа. В самом деле, предположим, что все числа нечет­ные. х ¹  – нечетное, у ¹  – нечетное. Следовательно, г – четное (так как сумма нечетных чисел всегда четна). Значит, все‑ таки одно (и только одно) из х, у, z должно делиться на 2.

А могут х и у быть нечетными? Нет, потому что у квадратов при делении на 4 будет остаток 1, а их сумма даст остаток 2, но г – четное, поэтому его квадрат при делении на 4 должен дать в остат­ке 0. Значит, в любой пифагоровой тройке после ее максимального сокращения число г будет нечетным. Для примера возьмем трой­ку (30, 40, 50). Она сводится к тройке (3, 4, 5), где 5 – нечетное число.

Вернемся к нашему выражению

 

, 2 _ Z – У Z + У

2'

Числа справа состоят из разных простых делителей. В каждое

из чисел простые множители могут входить хоть поодиночке, хоть

 

z – у z у

в степенях, но пересечении между разложениями –^– ^и –2– ^нет' Например,

z – у о ·

 

–– =Р_1Р%Р₃.. , р_к,

g И” 1J ^7

–2 = Ш1'Ш2'Ш₃... w _m.

(Вместо 5 и 7 здесь могут быть любые степени. )

С другой стороны, к ²  = qfq^ ■ ■ ■ q ² , поэтому

 

· · ·? / = P1P2PS ■ ■ ‑ Pkw\w2wl... w⁷_m.

Согласно основной теореме арифметики, существует единствен­ное разложение натурального числа на простые множители с точ­ностью до порядка сомножителей. Значит, по обе стороны от знака равенства стоят наборы одинаковых простых чисел. В частности, q ²  равен произведению двух чисел из правой части.

Так как пересечений простых множителей в наборах pi, ... , pk ш wi, ..., w _m  нет, то этот квадрат целиком «сидит» в одном из на­боров. Но то же самое можно сказать и про все прочие квадраты!

Поэтому все простые числа набора pi входят в разложение числа

z – у, „

–‑ – в четных степенях, и то же самое верно для набора Wj. Оле‑

^J Z – у Z + у

довательно, числа –^– ¹¹ –^– являются квадратами.

Это очень сильное утверждение (потому что квадратов очень мало среди натуральных чисел). 1, 4, 16, 25, 36, 49... – они встре­чаются все реже.

Введем новые обозначения. Так как наши выражения – ква­драты, то обозначим:

 

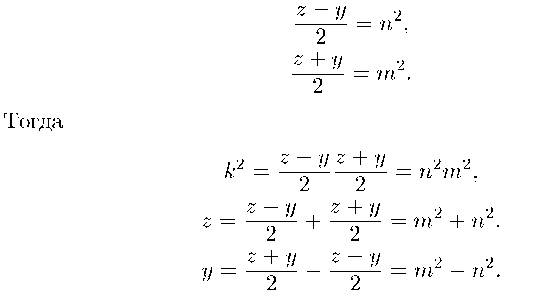
х ²  + у ²  = 4 т ² п ²  + m⁴ – 2 m ² n ²  + n⁴ = m⁴ + 2 m ² n ²  + n⁴ =

= (m² + n²)² = г².

Мы видим, что наша формула всегда дает «пифагоровы» трой­ки, но не обязательно положительные и взаимно простые.

Общая формула содержит два произвольных параметра. Для наглядности построим сетку (рис. 137).

 

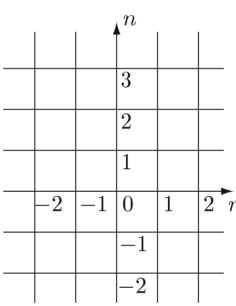
Рис. 137. Здесь спрятались все пифагоровы тройки!

В сетке выберем точку с координатами (0; 0) и оси: т впра­во, п вверх. Будем брать точки с координатами (т; п) и подста­влять их в нашу формулу. Например, возьмем точку (2; 1).

х = 2тп = 2 · 2 · 1 = 4,

у = _т ²  ‑ п ²  = 2² ‑ I² = 3, z = т ²  + п ²  = 2² + I² = 5.

Давайте возьмем что‑ нибудь более сложное. Напомню, что для по­лучения минимальных пифагоровых троек нам подходят только т п 0 с разной четностью.

Возьмем, например, (5; 2). Получим х = 20, у = 21, г = 29.

При подстановке мы увидим, что у нас появляются разные ви­ды треугольников. Узкие вытянутые треугольники, у которых ка‑ тот и гипотенуза отличаются на единицу: 12, 5, 13. Треугольники, у которых катеты почти равны друг другу: 20, 21, 29 (рис. 138).

 

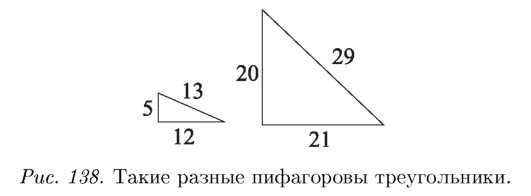
Какую точку па окружности даст нам треугольник 3, 4, 5? Точку (3/5; 4/5). Стороны 20, 21, 29 породят точку (20/29; 21/29). Для любой точки, которая попадает на окружность, сумма квадра­тов координат должна быть равна единице. Но не любая из этих точек рациональна.

Нужно найти все такие точки. Возьмем одну очевидную рацио­нальную точку с координатами (0, – 1).

Слушатель: А почему не (0; 1) или какую‑ то другую?

А. С: В принципе, можно выбрать какую угодно точку окружно­сти. Я выбрал такую точку, при которой формулы будут выглядеть проще всего.

Давайте предположим, что есть еще одна рациональная точка (х. у). Тогда прямая, которая проходит через эти две точки, имеет уравнение с рациональными коэффициентами (см. рис. 139). До­кажем это.

 

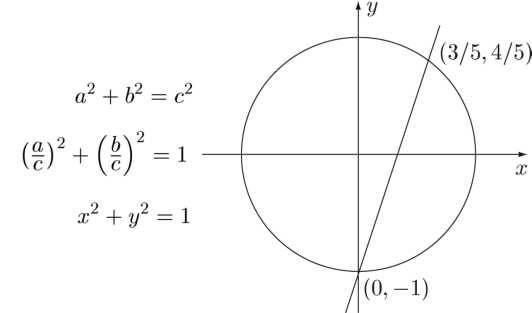
Рис. 139. Прямая, проходящая через точку (0, ‑ 1) и еще одну рациональ­ную точку, обладает рациональным коэффициентом наклона.

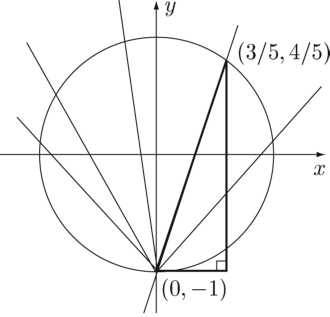
Давайте посмотрим, как выглядит уравнение прямой, проходя­щей через точку (0, –1) в общем случае. Вспомним, что у = кх+Ь уравнение прямой «с угловым коэффициентом и свободным чле­ном».

Если она проходит через точку (0, ‑ 1), то при подстановке х = 0, у = – 1 в наше уравнение мы должны получить верное равенство. Подставим: –1 = 0к + Ь, откуда Ь = – 1. то есть наше уравнение имеет вид у = кх – 1.

Мы получили общий вид прямой, проходящий через точку (0; –1). При разных к мы будем получать прямые с разным на­клоном (рис. 140).

 

случае рациональными числами, а отношение двух рациональных чисел является рациональным числом. Говорят, что рациональные числа «образуют поле», так как сумма, разность, произведение и частное дробей являются дробью.

Итак, если точка рациональная, то и наклон прямой, проходя­щей через нее и через точку (0; – 1) будет рациональным числом. Теперь мы докажем и обратное: если в формулу у = кх – 1 вме­сто к подставить любое рациональное число, то мы всегда получим в пересечении с окружностью две точки: (0; – 1) и какую‑ то другую рациональную точку.

Как найти точку пересечения прямой у = кх – 1 с окружностью х ²  + у ²  = 1?

Нужно решить систему уравнений

 

{у = кх – 1; х² + у² = 1.

Подставим значение у из первого уравнения во второе

х ²  + (кх – I)² = 1

и раскрываем скобки

х ²  + к ² х ²  – 2 кх + 1 = 1.

Упрощаем:

 

х² + к²х² = 2 кх.

Можно сократить на ж, так как случай х = 0 нам не интересен – он даст уже знакомую точку (0, ‑ 1):

 

х + к²х = 2 к.

Выразим теперь х и у через к:

 

ж(1 + к²) = 2к; х = 2к/(1 + к²),

 

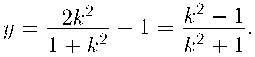
Из этих формул видно, что если к – рациональное число, то у их – тоже рациональные. Рациональные числа – это числа, с ко­торыми можно производить действия арифметической природы – плюс, минус, разделить, умножить. Рациональные числа от это­го остаются рациональными (то есть эти действия не выводят нас за пределы множества рациональных чисел).

Что значит «к – рациональное число»? Это значит, что к = Щ‑. Подставим вместо к дробь Щ, считая, что т, п – положительны,

 

fn

причем т п, а дробь – несократима:

 

 

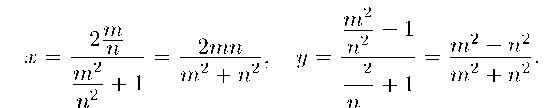
т

 

2

 

П

Осталось вспомнить, что в исходном уравнении х = а/с и у = Ь/с. Поэтому можно взять в качестве а числитель первой дроби, в ка­честве b – числитель второй дроби и в качестве с – их общий знаменатель. Получится: а = 2тп, Ь = т ²  – п ¹ , с = т ² + п². Одно из решений получается сразу, а прочие ему пропорциональны. Мы имеем тот же ответ, что и при первом способе решения. Внешне два метода, которыми мы решали эту задачу, совершенно не свя­заны друг с другом. Координаты и окружность нам показывают, какие множества высекают на плоскости те или иные алгебраиче­ские уравнения. А в первом способе была делимость и основная теорема арифметики. Она, являясь исключительно арифметиче­ским приемом, не имеет никакого отношения к геометрии. Стоит сказать, что если бы математики приходили к разным результа­там, решая одну и ту же задачу разными методами, то математика не была бы наукой. На деле же математика – это одно большое знание, связывающее разные методы между собой одним и тем же ответом.

Как видим, пифагоровы тройки нами разбиты «в пух и прах», но ость одна незадача. При к = 0 получается прямая, параллель­ная оси х (см. рис. 141).

 

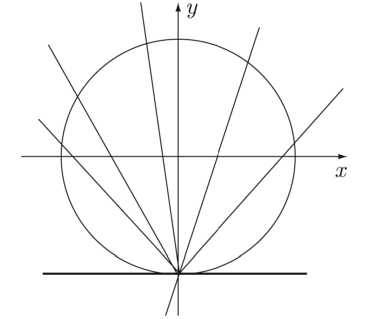
Рис. 141. Совпадение двух точек пересечения.

И вторая точка пересечения оказывается равной первой. Это как раз и отражает эффект касания. Алгебраические геометры, когда говорят о касании, всегда имеют в виду кратный корень, то есть корень, в котором совпали вместе несколько бывших некрат­ных решений.

Есть еще один любопытный момент. Есть еще одна рациональ­ная точка, которую мы не заметили на окружности. Точка (0, 1). Это решение появится у нас при к = ос.

Если мы хотим параметризовать окружность с помощью ра­циональных чисел, нужно, чтобы каждому рациональному числу соответствовала одна, и только одна точка на окружности. У нас же получается так, что на окружности есть лишняя точка, которая ни одному рациональному к не соответствует. В таком случае ма­тематики рассматривают не обычную прямую, а проективную. Мы уже сталкивались с проективной геометрией. В задаче на постро­ение с помощью линейки у нас точка пересечения пучка прямых уходила в бесконечность.

Таким образом, методы алгебраической геометрии часто связа­ны с проективной геометрией.

А теперь третий метод решения той же задачи – комплекс­ные числа. Мы разберем его на следующей лекции, а сейчас – обещанное введение в арифметику комплексных чисел.

Очень хочется разложить на множители х ²  + у ² . Мы умеем рас­кладывать разность квадратов. Попробуем представить нашу сум­му в виде разности:

2, 2 2 / 2\ х +у = _х  ^{^у ).

Если бы я мог извлечь корень из ^у², то смог бы разложить это выражение следующим путем:

 

х² + у² = х² – (–у²) = х² – (–1 у²) = (х – V–Iу)(х + V–I у)‑

В обычной жизни корень из – 1 не извлекается, но с помощью ком­плексных чисел это возможно. Пока мы исходим из желания полу­чить комплексное число наиболее естественным образом. Мы хо­тим разложить сумму квадратов на множители. Давайте считать, что есть такое число – 1, обозначим его за г. = *· Тогда

 

х² + у² = х² – (–у²) = х² – г² у² = (х – уг)(х + yi).

Это критически важно для многих задач. Например, для зада­чи о том, какие простые числа раскладываются в сумму двух квадратов. Число 41 – простое. Оно является суммой двух ква­дратов: 25 + 16; 41 = 5² + 4². Если мы умеем раскладывать та­кую сумму на множители, то у нас получатся любопытные вещи: 41 = (5 + 4г) (5 – 4*). Мы попадем в знакомую ситуацию, связанную с разложением числа 41 на множители, только теперь эти множи­тели – числа новой природы.

Число i – не является вещественным (то есть не лежит на обычной числовой прямой и не может использоваться для изме­рения физических величин) и, если мы нарисуем вещественную ось, оно будет находиться где‑ то вне нашей оси. Мы можем вы­брать сами, где его поместить. Удобнее всего поместить i на верти­кальной оси, выбрав некоторую плоскость, содержащую обычную вещественную ось (см. рис. 142).

 

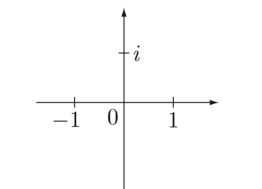
Рис. Ц2. Вот гдо притаилось загадочное число i.

Тогда получится, что любое число х + yi «живет на плоскости» в точке с координатами (х. у). Если мы хотим ввести в рассмотре­ние некоторую новую сущность, которая в квадрате дает минус единицу, то нам нужно уметь это число умножать на любые дей­ствительные числа. И такие произведения yi = z никогда не могут быть обычными числами, иначе само i = z/y превращалось бы в обычное число. А мы уже убедились в том, что i имеет «неве­щественную» природу. Кроме того, мы должны уметь выполнять действия сложения и вычитания между обычными (вещественны­ми или действительными) числами и числом i.

Давайте посмотрим. Беру вещественные числа и составляю вы­ражения:

 

(х + yi); (z + ti).

Вопрос: в каком случае эти два выражения задают одно и то же число? Попробуем действовать по привычным правилам.

 

х + yi = z + ti, х – z = ti – yi, x – z = i(t – y).

Если t = у, то из последнего равенства имеем х = г.

   

х – Z  

 

⇐ Предыдущая30313233343536373839Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: