Сумма двух точек плоскости строится так. Берем век­торы, порождаемые нашими точками, и складываем их по правилу параллелограмма.

Вычитание от сложения практически не отличается:

 

(х + yi) – (z + ti) = (х + yi) + (–z – ti) = (x – z) + i(y – t).

Вектор, порождаемый точкой (z. t), развернется в другую сторо­ну туда, где достроен смежный параллелограмм (рис. 146).

Итак, операции плюс и минус определены и всегда осуществи­мы. Также видно, что у каждого числа есть противоположное к по­му: (х + yi) и (–х – yi). С точки зрения сложения и вычитания система уже построена и ведет себя очевидным образом. Теперь переходим к гораздо более интересной теме. А именно: умноже­ние и деление комплексных чисел.

 

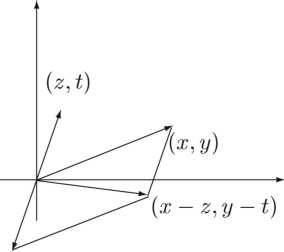
Рис. lJ _t 6. Вычитание комплексных чисел.

Я хочу узнать, как должно выглядеть умножение

 

(х + yi)(z + ti).

Будем пользоваться распределительным законом, который мате­матики называют дистрибутивным. Проще говоря, разрешается раскрывать скобки: а(Ь + с) = аЬ + ас (как учили в школе).

А также (о, + Ь)(с + d) = ас + Ьс + ad + bd.

Правило дистрибутивности вынуждает нас так умножать. По­тому что так делается в вещественных числах. Давайте попробуем перемножить два комплексных числа

 

(х + yi)(z + ti) = xz + xti + zyi + yti².

Теперь давайте вспомним, что г ²  = – 1,

 

(х + yi)(z + ti) = xz + xti + zyi + yti² =

= xz + xti + zyi – yt = (xz – yt) + (xt + yz)i.

Мы научились умножать. Произведением точек с координатами (х. у), (z. t) служит точка на плоскости с координатами (xz – yt, xt + yz).

Но этого для нас мало, потому что мы не видим, где «живет» на плоскости точка с такими координатами. Мы должны увидеть

ее, попять, как ее построить. Как получить ее из векторов, поро­ждаемых точками (ж, у), (z, t). Какие у этих векторов характери­стики? У них есть длины и углы поворота (отклонения ) от оси х. Пользуясь этими данными, мы должны получить новый вектор (xz – yt, xt + yz).

Нам нужно провести некоторое исследование. Для этого разра­ботаем терминологию.

У комплексного числа точки на плоскости первая коорди­ната называется вещественной частью, а вторая мнимой. Мни­мой ее называют потому, что, когда начинали с комплексными чи­слами общаться, считали, что числа i не существует. Существуют только вещественные числа. Остальные не существуют, они как бы у нас в воображении, imaginary numbers. С тех пор у комплексных чисел есть действительная и мнимая части.

Рассмотрим еще такую конструкцию. Для каждого вектора рисуется вектор, симметричный относительно вещественной оси. Точка (х: у) перейдет в точку (х, –у) (см. рис. 147).

 

Рис. Ц7. Векторы, симметричные относительно оси абсцисс.

Числу х + уг естественным образом сопоставляется число x – yi, которое лежит по другую сторону от вещественной оси.

Числа вида (х + уг) и (x – yi) называются сопряженным, и. Чему равно произведение этих чисел?

 

(х + yi)(x – yi) = х² + у².

Что такое х ²  + у ²  в геометрическом смысле? Это длина век­тора, обозначающего наше комплексное число, возведенная в ква­драт. Квадрат длины комплексного числа, рассматриваемого как вектор, равен произведению его самого и ему сопряженного.

И еще одна выкладка. Интересно, что получится, если я перем­ножу векторы, сопряженные к нашим исходным векторам:

 

(х – yi)(z – ti) = (xz – yt) – (xt + yz)i.

Вещественная часть не изменилась, а мнимая поменяла знак. Было (xz – yt, xt + yz), стало (xz – yt, –xt – yz). Получается, что если мы берем произвецение двух сопряженных, то полу­чается сопряженное к их произвецению (рис. 148).

 

Рис. lJ _t 8. Математики сказали бы так: умножение комплексных чисел «уважает» операцию сопряжения, и наоборот. Можно вначале сделать сопряжение каждого сомножителя, а потом перемножить их. а можно вначале перемножить, а после сделать сопряжение перемноженных. Ре­зультат будет одинаковым.

Хотелось бы уметь делить одну точку на плоскости на дру­гую точку. Это тоже совсем не сложно, если, конечно, не делить на ноль. Но на ноль мы и раньше не могли делить. Так что ни­чего удивительного в том, что мы не будем делить на 0, нет. Зна­чит, так. Попробуем разделить на число, которое не равно нулю.

Используем основное свойство дроби: дробь не изменится, если и числитель, и знаменатель умножить на одно и то же число. В качестве такого числа мы возьмем число, сопряженное к z + ti:

 

x + yi _ (х + yi)(z – ti) _ z + ti (z + ti)(z – ti)

_ (xz + yt) + (yz – xt)i _ xz + yt _| yz – xt. ~ ⁺

Итак, мы получили комплексное число в стандартном виде: веще‑

 

xz + yt, yz – xt

ственная – – и мнимая – – части.

 

z +t z +t

Всё. Теперь мы умеем делить, умножать, складывать и вычи­тать – всё как с обычными действительными числами. Однако мы пока не видим, как геометрически это выглядит, а это очень важно и чрезвычайно полезно.

Давайте все‑ таки это поймем. Для этого перемножим

 

(х + yi)(z + ti)(x – yi)(z – ti).

Если я буду перемножать почленно, то получится

   

(x+yi)(z+ti)(x‑ yi)(z‑ ti) = [(xz‑ yt)+(xt+yz)i][(xz‑ yt)‑ (xt+yz)i\.  

Обратите внимание, получились сопряженные комплексные чи­сла – значит, их произведение равно

 

(х + yi)(z + ti)(x – yi)(z – ti) =

= [{xz‑ yt) + (xt+yz)i][(xz^yt)^(xt+yz)i}) = (xz‑ yt)* + (xt, + yzf.

А если я вспомню, что от перемены мест множителей произведение не меняется, и переставлю скобки, то получу

 

[(_Ж + уг)(х ‑ yi)][(z ‑ ti))(z + ti)] = (х² + y²)(z² + t²).

Но мы же умножали одно и то же, значит, результаты совпадают:

 

(ж² + y²)(z² + t²) = (xz ‑ yt)² + (xt + yz)².

Это таинственное правило иногда изучается в школе как одно из правил сокращенного умножения. Но смысл его скрывается. Можно честно раскрыть все скобки и получить верное равенство. Совершенно честно, без всяких комплексных чисел. Но если вы сделаете это без комплексных чисел, то природа явления будет не видна и непонятна. А с номощыо комплексных чисел мы го­ворим. что (xz – yt) ²  + (xt + yz) ²  квадрат длины вектора, ко­торый является произведением исходных векторов (х, у) и (z. t). А (х ²  + у ² ) и (z ²  +t ² ) квадраты длин самих исходных векторов. Если я извлеку корень из этих длин, то получится, что

 

⇐ Предыдущая30313233343536373839Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: