длина вектора произведения равна произведению длин исходных векторов

длина вектора произведения равна произведению длин исходных векторов

 

sj (xz – yt)² + (xt + yz)² = sj (x² + y²)(z² + t²).

Мы узнали, что при перемножении комплексных чисел их длины перемножаются. Осталось выяснить, куда будет напра­влен вектор произведения. Вопрос, что же происходит с углами поворота каждого из сомножителей?

Сейчас я могу только сказать, что мое произведение лежит где‑ то на окружности радиуса, равного произведению длин наших векторов. Но где именно? Сейчас мы рассмотрим преобразование плоскости. Давайте нанесем на наши оси координат единичную окружность. На этой окружности «живут» точки 1. –1, i и –* (рис. 149).

 

Рис. 149. Единичная окружность на комплексной плоскости.

 

Рис. 150. Нижний катет равен cos tp, правый равен siny.

Точка данной окружности определяется углом, на который по­вернулся вектор единичной длины. Косинус это координата по оси X, синус по оси у. В учебниках пишут, что косинус это отношение прилежащего катета к гипотенузе. Но здесь гипоте­нуза имеет длину 1. Поэтому косинус равен просто горизонтально­му катету. А синус это отношение другого катета к гипотенузе. Гипотенуза имеет длину 1, и синус это просто второй катет.

А теперь я совершу обещанное преобразование: умножу все точ­ки плоскости на комплексное число cos р + imnp.

Напомню, что при умножении комплексных чисел длина полу­чаемого вектора равна произведению длин перемножаемых

   

sj(xz – yt)² + (xt + yz)² = sjx² + у² \Jz² + t².  

Подставим слева в формулу cos р и sin р вместо z к t

 

sj(х² + у²)(cos² (р + sin² ip) = \J(xz – yt)² + (xt + yz)².

Ho cos² p + sin² p = 1 (основное тригонометрическое тождество, следствие теоремы Пифагора). Получаем

 

\/(х² + У²)( 1) = \J(xz ‑ yt)² + (xt + yz)².

Мы домножаем па единицу, а значит, длина вектора не изменяется.

Получается, что при умножении на число cos ip + i sin ip любое комплексное число остается на той же окружности, на которой оно лежало.

Комплексное число «жило», например, в точке А, на рассто­янии \J х ²  + у' ²  от точки (0, 0); после преобразования оно будет «жить» на той же самой окружности в какой‑ то другой точке В. но на том же расстоянии от (0, 0) (см. рис. 151).

 

Похожим образом показывается, что для любых двух точек плоскости умножение на cos p+i sin 93 не изменит расстояния между ними.

 

 

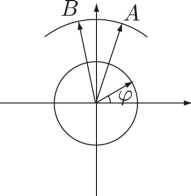
Рис. 151. В = A ‑ (cos tp + i sinyj)

Иными словами, умножение на число cos p+i sin р, примененное ко всем точкам плоскости, является движением плоскости.

Давайте попробуем понять, что же это за движение.

Для простоты изложения по ходу дела точки плоскости я буду называть комплексными числами, а комплексные числа точка­ми плоскости. Это позволит стереть некоторый налет «мнимости», остающийся в выражении комплексные числа.

Пусть qi = х + yi, qi = z + ti два комплексных числа, вто­рое из которых не равно ни нулю, ни единице, но при этом лежит на единичной окружности (то есть имеет модуль, или длину, рав­ную единице). Второе число, q‑ 2, мы на время всего рассуждения зафиксируем, а первое число, qi, будем «перебирать», подставляя всевозможные комплексные значения.

С помощью формулы Ц\Ц 2 мы сконструировали некоторое пре­образование точек плоскости: любая точка сц при этом преобра­зовании переходит в точку Ц\Ц 2 ‑ Ключевое утверждение состоит в том, что у этого преобразования будет только одна неподвижная точка: q\ = 0 (то есть только одна точка останется на месте).

Проведем доказательство этого утверждения. Допустим, какая‑ то точка q\ осталась на месте. Это означает, что q\ = qiq 2 ‑ Пере­несем оба выражения в левую часть, получим:

71 (1 ‑ ? 2) = 0.

Мы договорились, что q 2  ф 1, а тогда 1 – q 2 ф 0, и на этот множитель можно сократить обе части равенства. Следовательно, q\ = 0, что и утверждалось. Таким образом, наше преобразование плоскости является движением (что было установлено выше) и оставляет на месте ровно одну точку, а именно точку q\ = 0.

Один из примеров движения плоскости ровно с одной неподвиж­ной точкой хорошо известен: это – поворот на некоторый угол относительно неподвижной точки. Но, может быть, одними пово­ротами дело не ограничивается? Этот вопрос исследовал француз­ский математик М. Шаль. Оказалось, что ничего, кроме поворо­тов, в этой ситуации быть не может. Принимая его исследования на веру, 33 делаем вывод, что изучаемое преобразование является поворотом.

Итак, это движение – поворот. Остается вопрос, на какой угол мы повернули? Для ответа на этот вопрос вспомним, что число q 2 лежит на окружности, то есть равно cos р + г sin р при некотором значении угла р.

Я утверждаю, что наше движение является поворотом именно на угол р. Потому что точка qi = 1 перешла в точку qiq 2 = cos р + + i sin 9?. А раз единица в нее перешла, значит, мы повернули плос­кость на угол р. Ведь комплексное число q\ = 1 + 0* имело в на­чальный момент нулевой угол поворота.

Таким образом, любая точка переходит в точку, которая полу­чается поворотом па угол р соответствовавшего исходной точке вектора.

В частности, если я беру некоторый вектор и умножаю его на вектор cos р + i sin p, то он переходит в вектор, повернутый на угол р. Особый важный случай это умножение на вектор cos7r/2 + *sin7r/2, то есть просто на число i. Умножение вектора на i приводит к тому, что этот вектор поворачивается на 90°. Это особенно важно для тех технических вузов, где изучают ТОЭ (теоретические основы электротехники). Злые языки даже утвер­ждают, что перед основным экзаменом по ТОЭ там производится предэкзамен: у студента, заснувшего на лекции, над ухом стре­ляют хлопушкой и грозно спрашивают: УМНОЖЕНИЕ на *? Он должен сразу ответить: ПОВОРОТ НА 90 ГРАДУСОВ! (рис. 152).

 

Рис. 152. Умножение на i это поворот на 90°.

И окончательно. При умножении комплексных чисел углы складываются. Это правило, которое мы вывели, позволя­ет нам увидеть все арифметические операции над комплексными числами. А именно, при сложении комплексных чисел складыва­ем их как вектора по правилу параллелограмма. При умноже­нии длины векторов перемножаются, а углы поворотов скла­дываются. Слегка почесав в затылке, можно даже сказать так: при делении комплексных чисел их длины делятся, а углы поворота вычитаются друг из друга.

Сейчас будет бонус. Наконец‑ то мы запомним две зловредные формулы.

Давайте возьмем еще одну точку, лежащую на единичной окружности: сояф + isint/j. Куда она перейдет при умножении на cos р + i sin 93?

Она перейдет в точку той же окружности, но повернется на угол р. То есть суммарный угол для произведения будет (ф + ip). Получается, что произведение

(cos ip + i sin ip) (cos ф + i sin ф)

равно cos(p + ф) + i sin(9? + ф).

Теперь раскроем скобки:

(cos ip + i sin ip) (cos ф + i sin ф) =

= cos if cos ф + cos pi sin ф + i sin ip cos ф + i sin pi sin ф =

= (cos p cos ф – зтрзтф) + *(cos рзтф + sin93cos ф).

С другой стороны, это произведение равно cos(p + ф) + i sin(9? + ф). Получается, что

 

cos(p + ф) + i sin(9? + ф) =

= (cos р cos ф – зтрзтф) + *(cos рзтф + sin93cos ф).

Но если два комплексных числа равны друг другу, то веще­ственная часть равна вещественной, а мнимая – мнимой:

cos (р + ф) = cos^cos'i/; – зтрзтф, sin(9? + ф) = cos р sin ф + sin р cos ф.

Это и есть те «зловредные» формулы, которые доставляли вам головную боль в школе, всем поголовно. Они очень легко выводят­ся с использованием комплексных чисел.

 

⇐ Предыдущая30313233343536373839Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: