Некоторые соображения о преподавании математики в школе.

У каждого человека есть некие безумные идеи, в которые он свято верит. Я свято верю в то, что школьная математика должна быть устроена следующим образом.

Преподавание математики начинается с движений, причем сразу же вводится понятие группы движений – сперва прямой и окружности, затем плоскости. Давайте без обиняков это назы­вать своими именами – группа движений изучаемого объекта. Потом следует полная характеризация этих групп движений че­рез то, сколько у тех или иных движений имеется неподвижных точек.

Есть такая теорема «о трех гвоздях». Если три точки плоско­сти остаются неподвижными при движении, то движение является тождественным преобразованием, то есть оно вообще ничего не ме­няет. Для прямой и для окружности имеются очевидные аналоги этой теоремы, которые еще проще.

Завершим вкратце классификацию движений плоскости. Если у движения имеются две различные неподвижные точки, то непо­движной окажется и вся прямая, их соединяющая, а само пре­образование будет являться отражением относительно этой прямой. Если у движения ровно одна неподвижная точка, то это движение является поворотом. Если неподвижных точек нет, мы получаем два вида движения: параллельный перенос и сколь­зящая симметрия. Больше никаких движений плоскости нет.

Это – теорема Шаля, которая должна входить во все школь­ные программы. После того, как это прошли, нужно приступать к комплексным числам. Надо сразу сказать, что плоскость – это комплексные числа, образующие поле. Все основные алгебраи­ческие понятия должны быть введены прямо в детском саду, чтобы потом в школе уже было можно браться за дело34.

После изучения комплексных чисел выводятся правила умно­жения и сразу – переход к тригонометрии. Тригонометрия – это просто операции с комплексными числами, лежащими на окруж­ности.

А дальше можно переходить к более интересным вещам, напри­мер, к диофантовым уравнениям.

Обсудим, при чем тут комплексные числа (которых Диофант не знал) и диофантовы уравнения? На вещественной оси есть числа специальной природы, называемые целыми. Они «живут» на одинаковом расстоянии в обе стороны от 0 до бесконечности. Это числа 0, ±1, ±2, ±3, ±4 и так далее. Между ними «живут» вся­кие другие числа, которые нас пока сейчас интересовать не будут (рис. 153). Диофантовы уравнения это уравнения, которые на­до решать в рациональных либо в целых числах. Мы ограничимся целыми решениями. На прошлой лекции мы рассматривали сле­дующее уравнение

 

2, 2 2 X + у = Z.

Мы его решили двумя способами: с помощью анализа делимости в обычных целых числах и с помощью алгебраической геометрии. Есть еще и третий способ.

Рис. 153. Рошотка целых чисел на числовой оси (такого рода решетки бывают и на плоскости).

Подобно тому, как среди вещественных чисел можно выделить замечательное семейство целых, можно выделить не менее замеча­тельные семейства и среди комплексных чисел. Чем целые числа принципиально отличаются от вещественных? В них (во множе­стве целых чисел) нельзя делить. Иногда получается разделить, а иногда нет. Анализ того, что на что делится, приводит к со­держательной и красивой науке: к простым числам, к основной теореме арифметики и, в конечном счете, к решению этого самого уравнения х ²  + у ²  = z ² .

Теперь мы живем на плоскости, и хотелось бы сделать что‑ нибудь подобное во множестве комплексных чисел. Давайте по аналогии распространим целые числа на плоскость. Как будут выглядеть целые числа на плоскости? Скажу по секрету, что па плоскости имеется огромное количество числовых систем, ко­торые обобщают и продолжают целые числа. Можно построить числовые системы разными способами, и они все чрезвычайно важ­ны для многих диофантовых уравнений. Различные диофантовы уравнения требуют различных числовых систем. Но самое про­стое это рассмотреть комплексные числа, у которых просто обе части (и вещественная и мнимая) являются целыми числами (рис. 154).

 

Рис. 154‑ Загадочные гауссовы числа: среди них есть «простые», но как раз они‑ то и оказались самыми загадочными.

Узлы этой сетки и есть «целые числа» на плоскости. Первым их рассматривал Гаусс, мы назовем их Z[t\. Z – значит «целое», [*] – конкретное комплексное число, присовокупленное к целым.

Он к целым числам прибавил число i и спросил себя: а какие тогда должны быть числа еще взяты? Если мы взяли i и взяли 1, то мы должны, конечно, взять их сумму 1 + i. Потому что мы должны уметь складывать, вычитать и умножать (если хотим действовать по правилам обычных целых чисел). Ясно, что эти требования нас в конце концов приведут ко взятию произвольных целых кратных числа сложенных с любыми целыми (обычными) числами.

Числа вида а + Ы, где а, b – целые числа, называют гауссовыми числами. Складывать и вычитать их можно «покомпонентно», то есть (а + Ы) ± (с + di) = (а ± с) + (Ь ± d)i. При этом «на выходе» получаются снова Гауссовы числа, потому что сумма и разность целых чисел всегда являются целыми числами.

Но для полноценной работы с новыми числами нужно уметь их друг на друга умножать. Чудо состоит в том, что при перем­ножении Гауссовых чисел по обычным правилам перемножения комплексных чисел «на выходе» снова получаются Гауссовы, то есть целые комплексные числа. Читателю книги доставит удоволь­ствие самостоятельно перемножить два Гауссовых числа, чтобы увидеть, что целочисленность вещественной и мниной частей ре­зультата умножения сохраняется.

Кроме того, новые числа удовлетворяют всем тем же принци­пам умножения, вычитания и сложения, которые верны для обыч­ных целых чисел (потому что новые числа – это «подмножество» комплексных чисел, а последние этим правилам подчиняются).

В то же время из‑ за того, что мы акцентируем внимание на их «цельности», то есть целочисленности, у нас появляются нетриви­альные моменты, связанные с их делимостью друг на друга (анало­гично тому, как в системе обычных целых чисел разрабатывается теория делимости, теория простых чисел и разложение на простые множители).

В частности, можно определить понятие простого гауссова чи­сла.

Так вот, оказывается, что всё, что мы знаем про целые числа – делимость, простота, основная теорема арифметики – удивитель­ным образом переносится на '/■ {']■ то есть на систему Гауссовых чисел. Любое Гауссово а + Ы с целыми а и Ъ единственным обра­зом раскладывается в произведение простых чисел, которые уже ни на что не делятся.

Небольшое замечание: на числа 1, г, –1 и –г делятся все Гауссо­вы числа, так же, как в целых числах на прямой все числа делятся на 1 и – 1. Например, (а + Ы): % = b – ai. Это чуть‑ чуть услож‑ пяет ситуацию, потому что однозначность разложения на простые множители выполняется лишь с точностью до умножения и деле­ния на 1л’, –1 и –Потому что с точки зрения теории делимости (а + Ы) и {Ь – ai) это один и тот же простой множитель.

Для целых чисел на комплексной плоскости вообще появляет­ся много фокусов, которых не было для целых чисел на прямой. Например, число 2 перестало быть простым. Ибо оно раскладыва­ется на множители 2 = (1‑ И’)(1–*). Кстати, из геометрии это тоже следует (рис. 155).

 

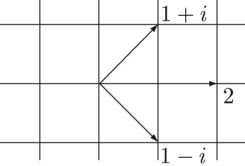
Рис. 155. Вот чудоса‑ то: сумма чисел (1 + г) и (1 – г) равна их произве­дению! Но обычное число 2 похитрее будет: 2 + 2 = 2‑ 2 = 2².

По правилу умножения мы должны взять произведение двух длин. Длина вектора 1 + i равна длине вектора 1 – и обе равны \/2. так как это гипотенуза прямоугольного треугольника с еди­ничными катетами. Значит, у произведения должна быть длина у/2 · у/2 = 2.

Посмотрим, что произойдет с углами. При умножении углы складываются. Но они у нас противоположные по знаку, значит, при сложении получится 0. То есть при умножении мы получим вектор длины 2, направленный по оси X. Обратите внимание, что мы невзначай нашли одно из решений уравнения в комплексных числах: г + w = zw (подпись к рис. 155).

Какие еще числа перестают быть простыми? Например, число 5. Теперь 5 = (2 + *)(2 – *) = 2² + Г². А число 3 можно разложить на множители или нет? Есть ли тут какое‑ то общее правило?

Оказывается, есть. Более того, ответ на заданный вопрос тес­нейшим образом связан с вопросом про «обычные» целые числа.

а именно: какие простые числа можно представить в виде суммы двух полных квадратов – то есть двух чисел, из которых можно нацело извлечь квадратный корень? Потрясающим образом этот вопрос решается введением Гауссовых чисел и изучением их ариф­метики.

Окинем еще раз взглядом наши построения. Мы ввели ком­плексные числа. Потом в них выделили семейство «целочислен­ных» комплексных чисел и назвали их гауссовыми. Там развили делимость, научились делить с остатком, обнаружили «Основную теорему арифметики». Зачем? Ответ таков: некоторые вопросы из арифметики обычных целых чисел можно решить только че­рез гауссовы числа.

Какие простые числа представляются в виде суммы двух ква­дратов? Эта задача чрезвычайно важная в теории кодирования. (Здесь под словом «кодирование» понимается запись информа­ции в таком виде, чтобы ее не смогли прочесть посторонние ли­ца. А «посторонние лица» обычно очень интересуются методами «взлома» использованного кода. ) Человек, который что‑ то знает про кодирование/декодирование, может взять и разрушить систе­му Пентагона в два щелчка мыши (вот вам и готов международный конфликт).

Вопросы математического кодирования – это вопросы пример­но такого же типа, как и задача о разложении простого числа в сумму двух квадратов. И вот долгожданный ответ на поставлен­ный выше вопрос.

Теорема. (Ферма – Эйлер – Гаусс. Гаусс здесь упомянут по­тому, что он ввел Гауссовы числа и установил простым образом все три эквивалентности, приводимые в формулировке. )

 

«Обычное» простое число (не комплексное) р является суммой двух квадратов, то есть р = х² + у² (х и у – обычные целые числа), тогда и только тогда, когда р перестает быть простым в гауссовой системе чисел Z[i ]. И происходит это тогда и толь­ко тогда, когда либо р = 2, либо число «р» имеет, остаток 1 при делении на 4, то есть р = 4fc + 1.

У Гаусса несколько «царских результатов». Он называл их раз­ными именами. Например, есть некий закон про поведение остат­ков при делении одних чисел на другие. Гаусс назвал его «золотым результатом», «золотой результат Гаусса». Связь между предста­вимостью простого числа р в виде суммы двух квадратов и его «поведением» в системе Гауссовых целых чисел – это королевская теорема Гаусса. Как следствие, «сокращая одну из эквивалентно­стей» в теореме выше, получаем как раз теорему Ферма – Эйле­ра: Простое число в обычных натуральных числах явля­ется суммой двух квадратов тогда и только тогда, когда оно имеет остаток 1 при делении на 4. Это мгновенно вы­числяемая характеристика. Например, 97. При делении на 4 дает остаток 1: 97 = 96 + 1 = 4 · 24 + 1. Значит, по нашей теореме оно должно представляться в виде суммы двух квадратов. Так и есть: 97 = 81 + 16 = 9² + 4².

Возьмите число, в котором 25 цифр. Проверьте, что оно имеет остаток 1 при делении на 4, это очень просто. Проверить, что оно простое, немножко сложнее, но тоже не очень долго. Так вот, если вы узнали, что оно простое, и вычислили, что оно имеет остаток 1 при делении на 4, то вы можете спорить на любую сумму с любым неверующим Фомой, что есть два числа, суммой квадратов кото­рых исходное число является. Никакого полного доказательства этой теоремы, кроме как через гауссовы числа, мне не известно (существует, говорят, по крайней мере 6 доказательств).

Давайте вернемся к пифагоровым тройкам. Пифагоровы тройки очень красиво находятся с помощью гауссовых чисел. Предполо­жим, есть тройка ж, у, z обычных целых чисел, которые являются сторонами прямоугольного треугольника, то есть

 

2, 2 2 Ж + у = Z.

Опять рассмотрим прямоугольный треугольник, наименьший в се­мействе. Иными словами, ж, у, г попарно взаимно просты, у них нет общих делителей. Тогда довольно просто показать, что (ж + уг) и (ж–yi) – также взаимно просты (это следует из разной четности ж и у).

То есть у гауссова числа и сопряженного ему гауссова числа нет общих делителей.

Вспоминаем прошлую лекцию: (х + уг)(х – уг ) = z ² .

Произведение равно квадрату некоторого числа. Значит, все (Гауссовы) простые множители числа г входят в него в четной степени. Это означает, что в левой части уравнения стоит, с точ­ностью до обратимых множителей, произведение двух квадратов.

Этот прием применяется во всех похожих структурах, не только в гауссовых числах. Если мы можем доказать основную теорему арифметики, то будет верен и этот замечательный результат: если произведение двух взаимно простых чисел равно квадрату, то ка­ждое из этих чисел является квадратом с точностью до умноже­ния на обратимые числа 1. /. – 1 и –i (для гауссовых чисел) или до умножения на любые другие обратимые числа (если целые чи­сла – не гауссовы).

Заметая «под ковер» исследование дополнительных обратимых множителей, делаем вывод, что

 

(х + yi) = (т + га)² = т² + 2 mni – п² = (т² – п²) + 2 mni.

Комплексные числа равны в том и только том случае, когда их вещественные и мнимые части равны:

 

х = т² – п², у = 2 тп.

Отсюда уже нетрудно вывести и формулу для гипотенузы Пифа­горова треугольника: г = т ²  + п ² .

Вот мы и получили «формулу индусов». Через гауссовы числа она выводится почти в одну строчку.

Теперь – пара слов про великую теорему Ферма. Такие ме­тоды, как тот, который мы сейчас рассматривали, развивавшие­ся весь XIX век, не привели к решению великой теоремы Ферма для всех показателей. Привело совершенно другое соображение. Соображение такое: если бы существовала тройка а, Ь, с такая, что а ^п  + Ъ ^п  = с”, то существовала бы некоторая, как математики выражаются, эллиптическая кривая с набором свойств, которые противоречат ее природе. Это – доказательство великой теоремы Ферма в одной фразе. Правда, к этой «одной фразе» придется до­бавить фраз 20‑ 30, чтобы хоть слегка пояснить, что это за зверь такой – эллиптическая кривая, и, главное, какое отношение она имеет к великой теореме Ферма.

Ну и последний сюжет.

Диофант решал самые разные уравнения. Некоторые он сфор­мулировал, но был не способен решить. А точнее, решения некото­рых из них не найдены в первых 6 томах. Мы ничего не знаем про оставшиеся 7 томов, и я не удивлюсь, если в них было всё, что по­том открывали в XVII, XVIII, XIX веках. В частности, Эйлер стал рассматривать одно из тех уравнений, которые Диофант не решил. Может, ли быть так, что квадрат некоторого натурального чи­сла отличается от куба другого натурального числа на единицу? То есть требуется решить в целых числах уравнение

а² = Ь³ ± 1.

То, что квадрат одного числа просто равен кубу другого, очень легко представить себе, если а = с³ и b = с², при некотором целом с. В самом деле, тогда

а² = (с³)² = _С6 = (с²)³ = Ь³.

Возьмем, например, с = 3. Тогда а, = 27, b = 9: 27² = 9³ = 729. Так что эта задача неинтересная. Правда, число 729 напоминает мне один разговор.

Однажды два математика беседовали в кафе. Один другому го­ворит: «На свете нет ни одного числа, которое не было бы чем‑ то удивительным, просто ни одного». А второй отвечает: «Ну, как же? Ну, я возьму навскидку 1729. Что интересного в числе 1729? » А второй посмотрел на него и сказал: «Ты сам не догадываешь­ся, насколько удивительное число ты назвал! Это первое из нату­ральных чисел, которое двумя разными способами представляется в виде суммы двух кубов».

Пальцем в небо ткнул и попал в число 1729. И вот что оказа­лось. Действительно, 1729 = 9³ + 10³, и 1729 = 12³ + I³. Второй математик был сражен этим аргументом.

Так вот, бывает ли, чтобы куб и квадрат отличались на единич­ку?

Допустим, ваш ребенок играет в кубики. Он сложил из них боль­шой куб, а вы украли у него один кубик. Тогда ребенок взял, раз­валил куб и сложил большой огромный квадрат. Может ли такое быть? Эйлер полностью решил эту задачу (а ²  = Ь³ ± 1).

Решим только одно уравнение из двух, потому что другое очень сложное: а² = Ь³ + 1 – сложное, а² = Ь³ – 1 простое.

В обоих случаях можно выписать ответ в явном виде.

У второго уравнения решений нет, кроме тривиальных: а = О и b = 1. Мы это сейчас докажем. А у первого, кроме тривиальных (а = 1 и b = 0), решением является пара (2, 3). Ведь З² = 2³ + 1. Других решений нет. Эйлер и это доказал, но весьма сложным путем.

Разберем простой вариант:

а ²  = Ь³ – 1, а ²  + 1 = Ь³, (а + i)(a – i) = Ь³.

Могут ли у (а + i) и (а – г) быть общие множители? Пусть (а + i) и (а – г) делятся на какое‑ то простое гауссово число. Тогда их разность

 

(а + г) – (а – i) = а + г – а + г = 2г

тоже на него делится.

Простых гауссовых чисел, которые делят число 2i, всего одно: (1 + г). Есть еще 1 – г, но это «то же самое простое число», ибо 1 – г = (–г)(1 + г) – то есть, одно получается из другого умноже­нием на обратимое.

Значит, наши числа (a + i) и (a – i), если они не взаимно просты, могут делиться только на (1+г). Но тогда их произведение делится на (1+*)² = 2г.   Значит, Ь делится на 2, а Ь³ – на 8. Но тогда а ²  будет иметь остаток 7 при делении на 8, так как а ²  + 1 = Ь³. А значит, остаток 3 при делении на 4. А, как мы выяснили на предыдущей лекции, таких квадратов не существует. При делении на 4 квадрат дает в остатке либо 1, либо 0. Поэтому такого быть не может.

Значит, ни одного общего делителя у чисел (а + i) и (а – i) нет. Их произведение является поэтому кубом некоторого гауссова числа. Согласно основной теореме арифметики, из этого следует, что каждое из них само является кубом гауссова числа (снова с точностью до умножения на обратимый элемент 1, i, –1 или i). Но все они тоже кубы, так что сформулированное утверждение верно в точности: скажем, а + г = (т + га)³.

Вдумайтесь, что мы сделали. Мы взяли обычное уравнение в це­лых числах. Зачем‑ то перешли в гауссовы числа и внутри гаус­совых чисел разложили левую часть на множители. После чего, живя внутри гауссовых чисел, мы сказали, что тогда

а + i = (т + га)³.

При этом а – целое не гауссово число. Гауссово число (а + i) живет на один шаг выше оси х.

Это число должно быть равно кубу некоторого гауссова числа. Теперь вспомним формулу куба суммы и раскроем скобки:

о о о 0 4

 

а + i = (т + га) = т + 3т ni – Зтп – п i =

= (т ³ – 3 тп ¹ ) + *(3m²n – п³).

Комплексные числа равны, значит равны их вещественная и мни­мая части:

а = т ³ – 3 mn², 1 = 3 т²п – п³.

Я вернулся из гауссовых чисел в обычные целые числа. С помо­щью гауссовых чисел я сделал вывод, который никогда в жизни не сделал бы без них. Из а² = Ь³ – 1 я получил, что

т²п – п³ = 1.

Теперь уже всё просто:

т ² п – п³ = 1, n(3m² – п ² ) = 1,

п и 3т ²  – п ²  – целые числа. Два числа дают в произведении 1 тогда и только тогда, когда они одновременно равны 1 или – 1.

п = ±1, 3 т ²  – п ²  = ±1.

Вы заметили, «единицу можно разложить на множители един­ственным способом: либо 1 умножить на 1, либо – 1 умножить на

1». Второй способ неотличим от первого, так как второе реше­ние можно сократить на «обратимое число» (–1). Так что второй случай кажется ненужным для рассмотрения – вроде как получа­ется избыточная аргументация. Но, как будет видно ниже, второй случай отнюдь не лишний.

Мой учитель Саша Шень рассказывал замечательную историю про то, как он стал математиком «из‑ за избыточной аргумента­ции». Ему подали рыбу, филе (я сам очень долго, лет до 30, ду­мал, что филе – это название рыбы). Так вот. Ему подали филе, и он сказал: «Мама, ну тут кости! Ты можешь вынуть кости? » А мама применила следующий замечательный логический прием, поставив его на дорогу математика. Она сказала: «Так! Саша, во‑ первых, это филе, и костей в нём быть не может. А во‑ вторых, где ты видел рыбу без костей? » Саша настолько был потрясен такой «железобетонной» логикой, что после этого стал математиком.

Итак, разберем наши два случая. Хотя они одинаковы с точки зрения единственности разложения на множители, но они не оди­наковы с точки зрения наличия решений!

Первый случай: п = 1, 3т ²  – п ²  = 1, следовательно, 3т ²  = 2. Но т – целое число. Значит, такого быть не может.

Второй случай: п = – 1, 3т ²  – п ²  = – 1, следовательно, 3т ²  = 0. Получаем т = 0.

а + г = (т + га)³ = (0 – *)³ = (^*)³ = г.

Так как а + i = г, то а = 0. Но Ь³ = а ²  + 1, значит, 6=1.

Это – единственное решение исходного уравнения. Получает­ся, что кроме тривиальных решений, других решений уравнения а ²   = Ь³ – 1 нет.

Из этой теории можно сделать следующий практический вывод. Если у вас с ребенком вышла такая ситуация, что он сложил из кубиков большой куб, вы украли у него кубик, и он сложит ква­драт, значит, что‑ то не так. Значит, он кубик «украл обратно» (и их было 729 скорее всего! ). Вы можете сказать: «Так, ты похитил у меня кубик! »

Как, папа? Как ты это увидел? Ты, наверное, ясновидя­щий. ..

Нет. Я просто умею решать диофантовы уравнения, сынок.

*Этот переход является психологически сложным. Подумайте над ним са­мостоятельно: квадрат – это такое число, в разложении которого на простые множители все простые числа входят в четных степенях.

 

[1]

[2]

[3]

[4]

[5]

[6]http: //pub. ist. ac. at/

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]неверное (по­пробуйте понять, почему! ).

[20]

[21]

[22] http: / /egamath. narod. ru/N quant /Collatz. htm.

[23]

[24]KR и KS имеют такой вид, мож­но с помощью подстановки в уравнения координат точек К, R и К, S соответ­ственно. Как известно, прямая однозначно определяется по любым двум своим различным точкам.

[25]

[26]любое движение сферы является либо поворотом, либо отражением.

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]Здесь Остапа понесло. Но в целом, если мы заменим детский сад на млад­шую школу, то все алгебраические понятия и в самом деле можно ввести на примере систем остатков от деления на некоторое фиксированное целое число!

 

⇐ Предыдущая30313233343536373839

Поделиться:

Воспользуйтесь поиском по сайту: