 |
Задание №1. Простейшие уравнения. Профильный ЕГЭ по математике
|
|
|
|
Задание №1. Простейшие уравнения. Профильный ЕГЭ по математике
В задании №1 варианта ЕГЭ вам встретятся всевозможные уравнения: квадратные и сводящиеся к квадратным, дробно-рациональные, иррациональные, степенные, показательные и логарифмические и даже тригонометрические. Видите, как много нужно знать, чтобы справиться с заданием! И еще ловушки и «подводные камни», которые ждут вас в самом неожиданном месте.
Вот список тем, которые стоит повторить:
Квадратные уравнения
Арифметический квадратный корень
Корни и степени
Показательная функция
Показательные уравнения
Логарифмическая функция
Логарифмические уравнения
Тригонометрический круг
Формулы приведения
Формулы тригонометрии
Простейшие тригонометрические уравнения 1
Уравнения, сводящиеся к квадратным
1. Решите уравнение 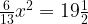 . Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
. Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
Кажется, что уравнение очень простое. Но иногда здесь ошибаются даже отличники. А вот шестиклассник бы не ошибся.
С левой частью уравнения все понятно. Дробь  умножается на
умножается на 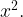 А в правой части — смешанное число
А в правой части — смешанное число  Его целая часть равна 19, а дробная часть равна
Его целая часть равна 19, а дробная часть равна 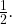 Запишем это число в виде неправильной дроби:
Запишем это число в виде неправильной дроби:
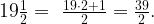
Получим:
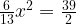


 или
или 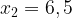
Выбираем меньший корень.
Ответ: - 6, 5.
2. Решите уравнение 
Возведем в квадрат левую часть уравнения. Получим:
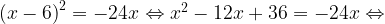

Ответ: - 6
Дробно-рациональные уравнения
3. Найдите корень уравнения
Перенесем единицу в левую часть уравнения. Представим 1 как  и приведем дроби к общему знаменателю:
и приведем дроби к общему знаменателю:
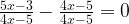
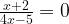
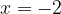
Это довольно простой тип уравнений. Главное - внимательность.
Иррациональные уравнения
Так называются уравнения, содержащие знак корня - квадратного, кубического или n-ной степени.
|
|
|
4. Решите уравнение:

Выражение под корнем должно быть неотрицательно, а знаменатель дроби не равен нулю.
Значит,  .
.
Возведём обе части уравнения в квадрат:

Решим пропорцию:

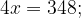
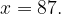
Условие  при этом выполняется.
при этом выполняется.
Ответ: 87.
5. Решите уравнение  Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
А в этом уравнении есть ловушка. Решите его самостоятельно и после этого читайте дальше.
Выражение под корнем должно быть неотрицательно. И сам корень — величина неотрицательная. Значит, и правая часть должна быть больше или равна нуля. Следовательно, уравнение равносильно системе:

Решение таких уравнений лучше всего записывать в виде цепочки равносильных переходов:


Мы получили, что 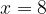 . Это единственный корень уравнения.
. Это единственный корень уравнения.
Типичная ошибка в решении этого уравнения такая. Учащиеся честно пишут ОДЗ, помня, что выражение под корнем должно быть неотрицательно:
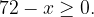
Возводят обе части уравнения в квадрат. Получают квадратное уравнение: 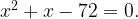 Находят его корни:
Находят его корни: 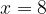 или
или 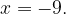 Пишут в ответ: -9 (как меньший из корней). В итоге ноль баллов.
Пишут в ответ: -9 (как меньший из корней). В итоге ноль баллов.
Теперь вы знаете, в чем дело. Конечно же, число -9 корнем этого уравнения быть не может.
6. Решите уравнение  . Если уравнение имеет более одного корня, в ответе запишите больший из корней.
. Если уравнение имеет более одного корня, в ответе запишите больший из корней.
Запишем решение как цепочку равносильных переходов.

Ответ: 9.
Показательные уравнения
При решении показательных уравнений мы пользуемся свойством монотонности показательной функции.
7. Решите уравнение 
Вспомним, что 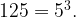 Уравнение приобретает вид:
Уравнение приобретает вид: 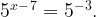 Функция
Функция  монотонно возрастает и каждое свое значение принимает только один раз. Степени равны, их основания, значит, и показатели равны.
монотонно возрастает и каждое свое значение принимает только один раз. Степени равны, их основания, значит, и показатели равны.
 откуда
откуда 
8. Решите уравнение 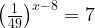
Представим  как
как 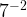

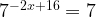
Функция  монотонно возрастает и каждое свое значение принимает только один раз. Степени равны, их основания, значит, и показатели равны.
монотонно возрастает и каждое свое значение принимает только один раз. Степени равны, их основания, значит, и показатели равны.
|
|
|
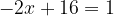


Ответ: 7, 5.
9. Решите уравнение 
Представим  в виде степени с основанием 3 и воспользуемся тем, что
в виде степени с основанием 3 и воспользуемся тем, что 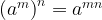
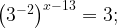

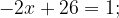

|
|
|


