 |
Логарифмические уравнения. Тригонометрические уравнения (Часть 1 ЕГЭ по математике)
|
|
|
|
Логарифмические уравнения
Решая логарифмические уравнения, мы также пользуемся монотонностью логарифмической функции: каждое свое значение она принимает только один раз. Это значит, что если логарифмы двух чисел по какому-либо основанию равны, значит, равны и сами числа.
И конечно, помним про область допустимых значений логарифма:
Логарифмы определены только для положительных чисел;
Основание логарифма должно быть положительно и не равно единице.
10. Решите уравнение:
Область допустимых значений: 
. Значит, 
Представим 2 в правой части уравнения как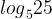 
- чтобы слева и справа в уравнении были логарифмы по основанию 5.
Функция 
монотонно возрастает и каждое свое значение принимает ровно один раз. Логарифмы равны, их основания равны. «Отбросим» логарифмы! Конечно, при этом
Ответ: 21.
11. Решите уравнение: 
Запишем решение как цепочку равносильных переходов. Записываем ОДЗ и «убираем» логарифмы:
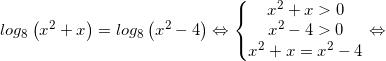
Ответ: -4.
12. Решите уравнение: 
Перейдем от логарифма по основанию 4 (в показателе) к логарифму по основанию 2. Мы делаем это по формуле перехода к другому основанию:
Записываем решение как цепочку равносильных переходов.
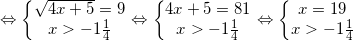
Ответ: 19.
13. Решите уравнение. Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
В этом уравнении тоже есть ловушка. Мы помним, что основание логарифма должно быть положительно и не равно единице.
Получим систему:
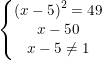
Первое уравнение мы получили просто из определения логарифма.
Квадратное уравнение имеет два корня: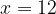 
и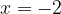 
Очевидно, корень 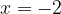является посторонним, поскольку основание логарифма должно быть положительным. Значит, единственный корень уравнения: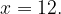 
|
|
|
Тригонометрические уравнения (Часть 1 ЕГЭ по математике)
Тригонометрические уравнения? В первой части вариантов ЕГЭ? - Да. Причем это задание не проще, чем задача 13 из второй части варианта Профильного ЕГЭ.
14. Найдите корень уравнения: 
В ответе запишите наибольший отрицательный корень.
Типичная ошибка — решать это уравнение в уме. Мы не будем так делать! Несмотря на то, что это задание включено в первую части варианта ЕГЭ, оно является полноценным тригонометрическим уравнением, причем с отбором решений.
Сделаем замену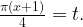 
Получим: 
Получаем решения: 
Вернемся к переменной x.
Поделим обе части уравнения на 
и умножим на 4.
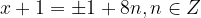
Первой серии принадлежат решения 
Вторая серия включает решения 
Наибольший отрицательный корень — тот из отрицательных, который ближе всех к нулю. Это 
Ответ: -2.
15. Решите уравнение 
В ответе напишите наименьший положительный корень.
Решение:
Сделаем замену 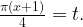Получим: 
Решения этого уравнения:
Вернемся к переменной х:
Умножим обе части уравнения на 4 и разделим на
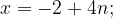
Выпишем несколько решений уравнения и выберем наименьший положительный корень:
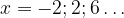Наименьший положительный корень 
Ответ: 2
Мы разобрали основные типы уравнений, встречающихся в задании №1 Профильного ЕГЭ по математике. Конечно, это не все, и видов уравнений в этой задаче существует намного больше. Именно поэтому мы рекомендуем начинать подготовку к ЕГЭ по математике не с задания 1, а с текстовых задач на проценты, движение и работу и основ теории вероятностей.
Успеха вам в подготовке к ЕГЭ!
Задание 2
Мы начнем с простых задач и основных понятий теории вероятностей.
Случайным называется событие, которое нельзя точно предсказать заранее. Оно может либо произойти, либо нет.
Вы выиграли в лотерею — случайное событие. Пригласили друзей отпраздновать выигрыш, а они по дороге к вам застряли в лифте — тоже случайное событие. Правда, мастер оказался поблизости и освободил всю компанию через десять минут — и это тоже можно считать счастливой случайностью…
|
|
|
Наша жизнь полна случайных событий. О каждом из них можно сказать, что оно произойдет с некоторой вероятностью. Скорее всего, вы интуитивно знакомы с этим понятием. Теперь мы дадим математическое определение вероятности.
Начнем с самого простого примера. Вы бросаете монетку. Орел или решка?
Такое действие, которое может привести к одному из нескольких результатов, в теории вероятностей называют испытанием.
Орел и решка — два возможных исхода испытания.
Орел выпадет в одном случае из двух возможных. Говорят, что вероятность того, что монетка упадет орлом, равна 
.
Бросим игральную кость. У кубика шесть граней, поэтому возможных исходов тоже шесть.
Например, вы загадали, что выпадет три очка. Это один исход из шести возможных. В теории вероятностей он будет называться благоприятным исходом.
Вероятность выпадения тройки равна 
(один благоприятный исход из шести возможных).
Вероятность четверки — тоже
А вот вероятность появления семерки равна нулю. Ведь грани с семью точками на кубике нет.
Вероятность события равна отношению числа благоприятных исходов к общему числу исходов.
Очевидно, что вероятность не может быть больше единицы.
Вот другой пример. В пакете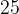 
яблок, из них 
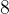— красные, остальные — зеленые. Ни формой, ни размером яблоки не отличаются. Вы запускаете в пакет руку и наугад вынимаете яблоко. Вероятность вытащить красное яблоко равна 
, а зеленое — 
.
Вероятность достать красное или зеленое яблоко равна 
.
|
|
|
