 |
Дробно-рациональные выражения. Формулы сокращенного умножения
|
|
|
|
Дробно-рациональные выражения. Формулы сокращенного умножения
Темы для повторения: Формулы сокращенного умножения, Приемы быстрого счета
Если вам встретится такое задание на ЕГЭ – значит, повезло!
1. Найдите значение выражения 
Не спешите перемножать десятичные дроби. Посмотрите на задачу внимательно.

Первый множитель в знаменателе умножили на 10, а второй поделили на 10 – просто передвинув запятую.
Ответ: 100
2. Найдите значение выражения 
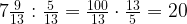
Ответ: 20
Корни и степени. Иррациональные выражения
Темы для повторения: Арифметический квадратный корень.
Арифметический квадратный корень из числа  — это такое неотрицательное число, квадрат которого равен
— это такое неотрицательное число, квадрат которого равен  .
.
 .
.
3. Вычислите  .
.
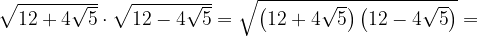

Применили одну из формул сокращенного умножения.
Ответ: 8
4. Вычислите:

Упростим множители:
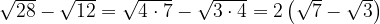


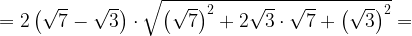

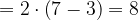
Ответ: 8.
Действия со степенями
Темы для повторения:
Вспомним правила действий со степенями.


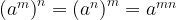

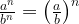
5. Найдите значение выражения:  при
при 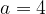

Применили формулу частного степеней 
6. Вычислите 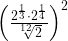
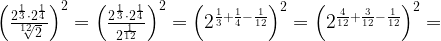

7. Вычислите  , если
, если 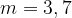 .
.
Спокойно, не пугаемся. И конечно, не спешим подставлять значение  Сначала упростим выражение.
Сначала упростим выражение.

8. Вычислите 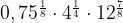

Применили формулу для произведения степеней: 
9. Вычислите 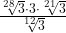
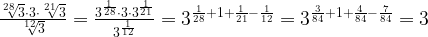
Записали корни в виде степеней (это удобно! ) и применили формулу произведения степеней.
Логарифмические выражения
Темы для повторения:
Логарифмы
Логарифм положительного числа  по основанию
по основанию  — это показатель степени, в которую надо возвести
— это показатель степени, в которую надо возвести  , чтобы получить
, чтобы получить  .
.
 .
.
При этом  > 0,
> 0,  > 0,
> 0, 
Основные логарифмические формулы:
Основное логарифмическое тождество: 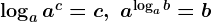
Логарифм произведения равен сумме логарифмов: 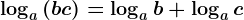
Логарифм частного равен разности логарифмов: 
|
|
|
Формула для логарифма степени: 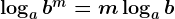
Формула перехода к новому основанию: 
10. Вычислите: 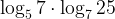 .
.

Снова формула перехода к другому основанию.
 , поэтому
, поэтому
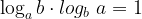
11. Найдите  , если
, если 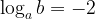 .
.

12. Найдите значение выражения  .
.

13. Найдите значение выражения  .
.
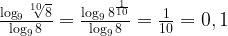 .
.
14. Найдите значение выражения  .
.
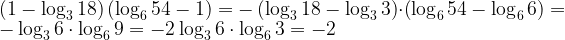 .
.
Тригонометрия. Формулы тригонометрии и формулы приведения
Темы для повторения:
Тригонометрический круг.
Формулы тригонометрии.
Формулы приведения.
15. Вычислите: 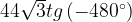
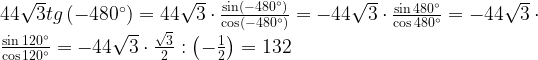
16. Найдите  , если
, если 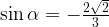 и
и  .
.

Т. к.  , то
, то 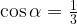

17. Найдите  , если
, если 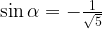 и
и 

Т. к.  , то
, то


18. Найдите значение выражения: 


Применили формулу приведения.
19. Упростите выражение: 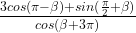
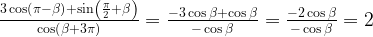
Применили формулу приведения.
20. Найдите  , если
, если  .
.
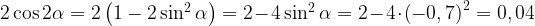
21. Вычислите  , если
, если 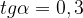
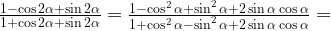

Алгебраические выражения, корни, степени и логарифмы. И еще тригонометрия. Это всё, что может встретиться в задании 9 Профильного ЕГЭ по математике?
Оказывается, и это не всё! Еще нужно знать, что такое модуль. И как найти 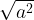 .
.
Другие типы заданий
Темы для повторения:
Модуль числа.
Что такое функция.
22. Найдите значение выражения
 при
при  .
.
Запомним: 
 .
.
Если  , то
, то  и
и  .
.
При этом  и
и 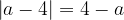 .
.
При  получаем:
получаем:  .
.
Ответ: 2
23. Найдите значение выражения
 при
при  .
.
При  получим:
получим:
 .
.
Ответ: 12.
24. Найдите  , если
, если  , при
, при 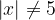 .
.
Что такое  ? Это функция, каждому числу ставящая в соответствие число
? Это функция, каждому числу ставящая в соответствие число 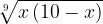 . Например,
. Например,  ;
;

Тогда:
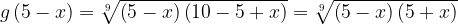 ,
,

Заметим, что  .
.
Значит, при 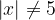
 .
.
25. Найдите  , если
, если 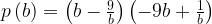 , при
, при  .
.
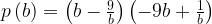 — функция, каждому числу b ставящая в соответствии число
— функция, каждому числу b ставящая в соответствии число
 .
.
Тогда при 
 , и значение выражения
, и значение выражения  равно 1.
равно 1.
Задание 5
Задание 5 Профильного ЕГЭ по математике – это основы стереометрии. Это задачи на вычисление объемов и площадей поверхности многогранников и тел вращения.
Ничего сложного здесь нет. Все эти задачи доступны даже десятикласснику. И даже гуманитарию.
Как решать задания по стереометрии из первой части Профильного ЕГЭ?
Повторим формулы для вычисления объемов и площадей поверхности многогранников (призмы, пирамиды… ) и тел вращения (цилиндра, конуса и шара)
|
|
|
Проверим себя – умеем ли мы рисовать чертежи?
Посмотрим, как решаются простые задачи по стереометрии и задачи с секретами.
Запоминаем один из главных лайфхаков решения задач по стереометрии:
Отношение объемов подобных тел равно кубу коэффициента подобия.
Если все линейные размеры объемного тела увеличить в k раз, то его площадь увеличится в  раз, а объем в
раз, а объем в 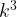 раз.
раз.



И решаем задачи. У нас все получится!
1. Во сколько раз увеличатся площадь поверхности и объем куба, если его ребро увеличить в два раза?
Отношение площадей поверхности подобных тел равно квадрату коэффициента подобия, а отношение объемов – кубу коэффициента подобия. При увеличении ребра в 2 раза площадь поверхности увеличится в 4 раза, а объем – в 8 раз.
2. Площадь основания конуса равна 18. Плоскость, параллельная плоскости основания конуса, делит его высоту на отрезки длиной 3 и 6, считая от вершины. Найдите площадь сечения конуса этой плоскостью.

Плоскость, параллельная основанию, отсекает от конуса меньший конус, все линейные размеры которого в 3 раза меньше, чем у большого. Поэтому площадь сечения в 9 раз меньше площади основания. Она равна 2.
3. Объем пирамиды равен 10. Через середину высоты параллельно основанию пирамиды проведено сечение, которое является основанием меньшей пирамиды с той же вершиной. Найдите объем меньшей пирамиды.
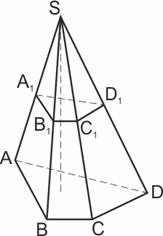
Меньшая пирамида подобна большой, коэффициент подобия  Отношение объемов подобных тел равно кубу коэффициента подобия. Поэтому объем меньшей пирамиды в 8 раз меньше объема исходной пирамиды. Он равен
Отношение объемов подобных тел равно кубу коэффициента подобия. Поэтому объем меньшей пирамиды в 8 раз меньше объема исходной пирамиды. Он равен 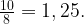
4. Объём правильной четырёхугольной пирамиды SABCD равен 116. Точка E — середина ребра SB. Найдите объём треугольной пирамиды EABC.
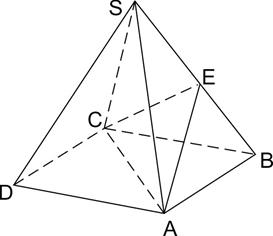
Площадь основания пирамиды ЕАВС в 2 раза меньше, чем у пирамиды ABCDS. Высота пирамиды ЕАВС равна половине высоты пирамиды ABCDS. Значит, объем пирамиды ЕАВС в 4 раза меньше объема пирамиды ABCDS. Он равен 
5. В правильной четырехугольной пирамиде SABCD точка E – середина ребра AB, боковое ребро SC равно 4, длина отрезка SE равна 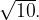 Найти объем пирамиды SABCD.
Найти объем пирамиды SABCD.

Найдем сторону основания пирамиды. По теореме Пифагора, для треугольника SAE получаем, что  Соответственно, сторона основания пирамиды равна
Соответственно, сторона основания пирамиды равна 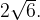 Если обозначить центр основания за H, то высоту пирамиды найдем по теореме Пифагора для треугольника SHE – она равна 2.
Если обозначить центр основания за H, то высоту пирамиды найдем по теореме Пифагора для треугольника SHE – она равна 2.
|
|
|
Применяя формулу для объема пирамиды  , получаем ответ: 16.
, получаем ответ: 16.
Многие задания №8 Профильного ЕГЭ по математике можно считать подготовительными – для того, чтобы научиться решать задачу 14 из второй части ЕГЭ.
Для решения некоторых из них стоит выучить основные определения и теоремы стереометрии. В общем, то, что входит в программу по стереометрии.
6. Стороны основания треугольной пирамиды равны 15, 16 и 17. Боковые ребра наклонены к плоскости основания под углами 45°. Найдите объем пирамиды.
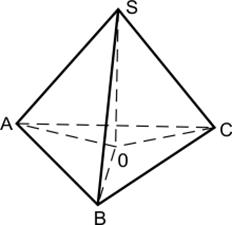
Пусть точка О – проекция точки S на плоскость основания пирамиды. Прямоугольные треугольники АОS, ВОS, СОS равны (по общему катету ОS и острому углу). Значит, АО = ВО = СО. Точка О, равноудаленная от вершин основания, – это центр окружности, описанной вокруг треугольника АВС. Тогда АО = ВО = СО = OS = R, где R – радиус этой окружности.
Радиус описанной окружности найдем по формуле

Площадь  найдем по формуле Герона:
найдем по формуле Герона:
 , где
, где  – полупериметр.
– полупериметр.
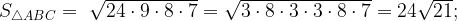
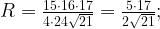

Заметим, что если боковые ребра пирамиды наклонены к плоскости основания под одинаковым углом, то вершина проецируется в центр основания.
7. В правильной треугольной призме 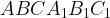 , все ребра которой равны 3, найдите угол между прямыми
, все ребра которой равны 3, найдите угол между прямыми  и
и  Ответ дайте в градусах.
Ответ дайте в градусах.

Угол между скрещивающимися прямыми равен углу между параллельными им прямыми, лежащими в одной плоскости. Поскольку 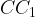 и
и  параллельны, найдем угол между
параллельны, найдем угол между 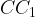 и
и  . Он равен 45 градусов, так как грань – квадрат.
. Он равен 45 градусов, так как грань – квадрат.
Ответ: 45.
Задание 6
Необходимая теория:
Производная функции
Таблица производных
Первообразная функции
Задание 6 Профильного ЕГЭ по математике — это задачи на геометрический и физический смысл производной. Это задачи о том, как производная связана с поведением функции. И еще (правда, очень редко) в этих встречаются вопросы о первообразной.
|
|
|


