 |
События А и В называют независимыми, если вероятность появления события А не меняет вероятности появления события В.
|
|
|
|
События А и В называют независимыми, если вероятность появления события А не меняет вероятности появления события В.
В нашей задаче так и есть: неразумный паук сворачивает налево или направо случайным образом, независимо от того, что он делал до этого.
Для нескольких независимых событий вероятность того, что все они произойдут, равна произведению вероятностей.
(А) Два грузовика, работая совместно, вывозят снег с улицы Нижняя Подгорная, причем первый грузовик должен сделать три рейса с грузом снега, а второй - два. Вероятность застрять с грузом снега при подъеме в горку равна 0, 2 для первого грузовика и 0, 25 - для второго. С какой вероятностью грузовики вывезут снег с улицы Нижняя Подгорная, ни разу не застряв на горке?
Вероятность для первого грузовика благополучно одолеть горку 
Для второго 
Поскольку первый грузовик должен сделать 3 рейса, а второй – два, грузовики ни разу не застрянут на горке с вероятностью 
Агрофирма закупает куриные яйца в двух домашних хозяйствах. 40% яиц из первого хозяйства — яйца высшей категории, а из второго хозяйства — 20% яиц высшей категории. Всего высшую категорию получает 35% яиц. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.
Нарисуем все возможные исходы ситуации. Покупатель пришел в магазин, который принадлежит агрофирме, и купил яйцо. Надо найти вероятность того, что это яйцо из первого хозяйства.
Яйца могут быть только или из первого домашнего хозяйства, или из второго, причем эти два события несовместны. Других яиц в этот магазин не поступает.
Пусть вероятность того, что купленное яйцо из первого хозяйства, равна 
. Тогда вероятность того, что яйцо из второго хозяйства (противоположного события), равна 
.
|
|
|
Яйца могут быть высшей категории и не высшей.
В первом хозяйстве 40% яиц имеют высшую категорию, а 60% - не высшую. Это значит, что случайно выбранное яйцо из первого хозяйства с вероятностью 40% будет высшей категории.
Во втором хозяйстве 20% яиц высшей категории, а 80% - не высшей.
Пусть случайно выбранное в магазине яйцо - из первого хозяйства и высшей категории. Вероятность этого события равна произведению вероятностей: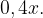 
Вероятность того, что яйцо из второго хозяйства и высшей категории, равна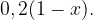 
Если мы сложим эти две вероятности, мы получим вероятность того, что яйцо имеет высшую категорию. По условию, высшую категорию имеют 35% яиц, значит, эта вероятность равна 0, 35.
Мы получили уравнение:
Решаем это уравнение и находим, что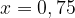 
– вероятность того, что яйцо, купленное у этой агрофирмы, оказалось из первого хозяйства.
Всем пациентам с подозрением на гепатит делают анализ крови. Если анализ выявляет гепатит, то результат анализа называется положительным. У больных гепатитом пациентов анализ даёт положительный результат с вероятностью 0, 9. Если пациент не болен гепатитом, то анализ может дать ложный положительный результат с вероятностью 0, 01. Известно, что 5% пациентов, поступающих с подозрением на гепатит, действительно больны гепатитом. Найдите вероятность того, что результат анализа у пациента, поступившего в клинику с подозрением на гепатит, будет положительным.
С чем пришел пациент в клинику? – С подозрением на гепатит. Возможно, он действительно болен гепатитом, а возможно, у его плохого самочувствия другая причина. Может быть, он просто съел что-нибудь. Вероятность того, что он болен гепатитом, равна 0, 05 (то есть 5%). Вероятность того, что он здоров, равна 0, 95 (то есть 95%).
Пациенту делают анализ. Покажем на схеме все возможные исходы:
|
|
|
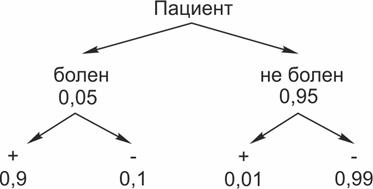
Если он болен гепатитом, анализ дает положительный результат с вероятностью 0, 9. То есть анализ покажет: «есть гепатит».
Заметим, что анализ не во всех случаях выявляет гепатит у того, кто действительно им болен. С вероятностью 0, 1 анализ не распознает гепатит у больного.
Более того. Анализ может ошибочно дать положительный результат у того, кто не болеет гепатитом. Вероятность такого ложного положительного результата 0, 01. Тогда с вероятностью 0, 99 анализ даст отрицательный результат, если человек здоров.
Найдем вероятность того, что результат анализа у пациента, поступившего в клинику с подозрением на гепатит, будет положительным.
Благоприятные для этой ситуации исходы: человек болен, и анализ положительный (вероятность одновременного наступления этих двух событий равна 
), или человек здоров, и анализ ложный положительный (вероятность одновременного наступления этих двух событий равна 
). Так как события «человек болен» и «человек не болен» несовместны, то вероятность того, что результат анализа будет положительным, равна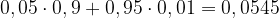 
Ответ: 0, 0545.
Чтобы поступить в институт на специальность «Лингвистика», абитуриент З. должен набрать на ЕГЭ не менее 70 баллов по каждому из трёх предметов — математика, русский язык и иностранный язык. Чтобы поступить на на специальность «Коммерция», нужно набрать не менее 70 баллов по каждому из трёх предметов — математика, русский язык и обществознание.
Вероятность того, что абитуриент З. получит не менее 70 баллов по математике, равна 0, 6, по русскому языку — 0, 8, по иностранному языку — 0, 7 и по обществознанию — 0, 5.
Найдите вероятность того, что З. сможет поступить хотя бы на одну из двух упомянутых специальностей.
Заметим, что в задаче не спрашивается, будет ли абитуриент по фамилии З. учиться и лингвистике, и коммерции сразу и получать два диплома. Здесь надо найти вероятность того, что З. сможет поступить хотя бы на одну из двух данных специальностей – то есть наберет необходимое количество баллов.
Для того чтобы поступить хотя бы на одну из двух специальностей, З. должен набрать не менее 70 баллов по математике. И по русскому. И еще – обществознания или иностранный.
Вероятность набрать 70 баллов по математике для него равна 0, 6.
Вероятность набрать баллы по математике и русскому равна 
|
|
|
Разберемся с иностранным и обществознанием. Нам подходят варианты, когда абитуриент набрал баллы по обществознанию, по иностранному или по обоим. Не подходит вариант, когда ни по языку, ни по «обществу» он не набрал баллов. Значит, вероятность сдать обществознание или иностранный не ниже чем на 70 баллов равна
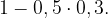
В результате вероятность сдать математику, русский и обществознание или иностранный равна 
Это ответ.
Чтобы полностью освоить тему, смотрите видеокурс по теории вероятностей. Это бесплатно.
Еще задачи ЕГЭ по теме " Теория вероятностей"
Смотрите также: парадокс Монти Холла
Задание 3
Это одно из сложных заданий первой части Профильного ЕГЭ по математике. Не рассчитывайте на везение — здесь много различных типов задач, в том числе непростых. Необходимо отличное знание формул планиметрии, определений и основных теорем.
Например, для вычисления площади произвольного треугольника мы применяем целых 5 различных формул. Cколько из них вы помните?
Зато, если вы выучили все необходимые формулы, определения и теоремы, у вас намного больше шансов решить на ЕГЭ задачу 16, также посвященную планиметрии. Многие задания под №3 являются схемами для решения более сложных геометрических задач.
Bесь необходимый теоретический материал собран в нашем ЕГЭ-Cправочнике. Поэтому сразу перейдем к практике и рассмотрим основные типы заданий №3 Профильного ЕГЭ по математике.
|
|
|
