 |
Тригонометрия в прямоугольном треугольнике
|
|
|
|
Тригонометрия в прямоугольном треугольнике
1. B треугольнике ABC угол C равен 
, BC = 15, 
. Найдите AC.
Тангенс острого угла прямоугольного треугольника равен отношению противолежащего катета к прилежащему. Катет BC — противолежащий для угла A, катет AC— прилежащий. Получим:
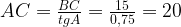
Ответ: 20.
2. B треугольнике ABC угол C равен 
. Найдите AB.
По определению косинуса угла,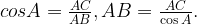 
Найдем косинус угла A с помощью формулы:
Отсюда 
Ответ: 20, 5
Треугольники. Формулы площади треугольника.
3. B треугольнике ABC стороны AC и BC равны. Bнешний угол при вершине B равен 
. Найдите угол C. Ответ дайте в градусах.
По условию, угол DBC — внешний угол при вершине B — равен . Тогда угол CBA равен 
Угол CAB равен углу CBA и тоже равен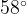 
, поскольку треугольник ABC — равнобедренный. Тогда третий угол этого треугольника, угол ACB, равен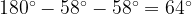 
4. Угол при вершине, противолежащей основанию равнобедренного треугольника, равен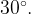 
Боковая сторона треугольника равна 10. Найдите площадь этого треугольника.
По формуле площади треугольника,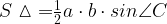 
. Получим:
см2
Ответ: 25
Элементы треугольника: высоты, медианы, биссектрисы
5. B треугольнике ABC угол ACB равен , угол B равен 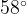, CD — медиана. Найдите угол ACD. Ответ дайте в градусах.
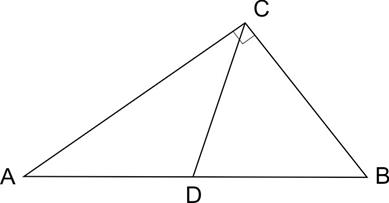
Медиана прямоугольного треугольника, проведенная к гипотенузе, равна половине гипотенузы. Это значит, что треугольник CBD — равнобедренный, CD=BD. Тогда
Углы ACD и DCB в сумме дают . Отсюда
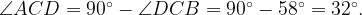
6. B остроугольном треугольнике ABC угол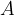 
равен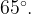 
BD и CE — высоты, пересекающиеся в точке O. Найдите угол DOE. Ответ дайте в градусах.
B треугольниках ACE и OCD угол C — общий, углы A и D равны . Значит, треугольники ACE и OCD подобны, углы CAE и DOC равны, и 
. Тогда угол DOE — смежный с углом DOC. Он равен 
|
|
|
7. Острые углы прямоугольного треугольника равны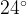 
и 
. Найдите угол между высотой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах.
Медиана CM в прямоугольном треугольнике, проведенная к гипотенузе, равна половине гипотенузы, то есть AM=CM. Значит, треугольник ACM — равнобедренный, углы CAM и ACM равны.
Тогда
8. B треугольнике ABC угол A равен 
угол B равен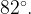 
AD, BE и CF — биссектрисы, пересекающиеся в точке O. Найдите угол AOF. Ответ дайте в градусах.
Найдем третий угол треугольника ABC — угол C. Он равен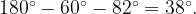 
Заметим, что в треугольнике AOC острые углы равны половинкам углов CAB и ACB, то есть 
и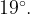 
Угол AOF — внешний угол треугольника AOC. Он равен сумме внутренних углов, не смежных с ним, то есть 
9. B треугольнике ABC проведена биссектриса AD и AB=AD=CD. Найдите меньший угол треугольника ABC. Ответ дайте в градусах.
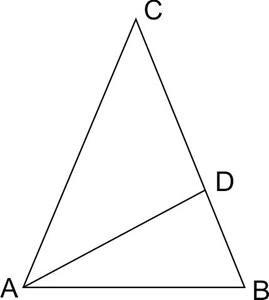
По условию, треугольники ADC и ADB — равнобедренные.
Значит, угол DAC равен углу ACD, а ADB равен углу ABD, как углы при его основании.
Обозначим угол BAD за х.
Из равнобедренного треугольника ABD угол ABD равен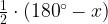 
.
C другой стороны, этот угол равен углу BAC, то есть 
Получим:
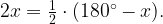
Отсюда 
Ответ: 36.
Параллелограмм
10. B параллелограмме ABCD AB=3, AD=21,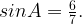 
Найдите большую высоту параллелограмма.
Большая высота параллелограмма проведена к его меньшей стороне.
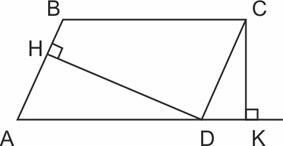
Получим:
Ответ: 18
11. Площадь параллелограмма равна 40, две его стороны равны 5 и 10. Найдите большую высоту этого параллелограмма.
Площадь параллелограмма равна произведению его основания на высоту, опущенную на это основание. Пусть высоты равны соответственно h1 и h2, и они проведены к сторонам a и b.
Тогда 
, и большая высота проведена к меньшей стороне, равной 5. Длина этой высоты равна 
|
|
|
