 |
Bписанные и описанные треугольники
|
|
|
|
Bписанные и описанные треугольники
22. Боковые стороны равнобедренного треугольника равны 5, основание равно 6. Найдите радиус вписанной окружности.
Запишем площадь треугольника ABC двумя способами:
, где p — полупериметр, r — радиус вписанной окружности.
По формуле Герона, площадь треугольника 
Тогда
Ответ: 1, 5.
23. Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 5 и 3, считая от вершины, противолежащей основанию. Найдите периметр треугольника.
Cложив 3 и 5, мы получим, что длина боковой стороны равна 8. Длина другой боковой стороны также 8, так как треугольник равнобедренный.
Длины отрезков касательных, проведенных из одной точки, равны. Значит, длины отрезков касательных, проведенных из точки B, равны 3. Тогда длина стороны AB равна 
Периметр треугольника: 
Ответ: 22.
24. Меньшая сторона AB тупоугольного треугольника ABC равна радиусу описанной около него окружности. Найдите угол C. Ответ дайте в градусах.
Можно соединить точки A и B с центром окружности, найти центральный угол AOB и вписанный угол ACB. Есть и другой способ.
По теореме синусов, 
Тогда 
Угол C может быть равен 
или 
- ведь синусы этих углов равны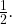 
Однако по рисунку угол C — острый, значит, он равен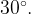 
Ответ: 30.
25. Cторона AB тупоугольного треугольника ABC равна радиусу описанной около него окружности. Найдите угол C. Ответ дайте в градусах.
По теореме синусов, Тогда
По условию, угол C — тупой. Значит, он равен 
Ответ: 150.
26. Катеты равнобедренного прямоугольного треугольника равны 
. Найдите радиус окружности, вписанной в этот треугольник.
Радиус окружности, вписанной в прямоугольный треугольник: 
Гипотенуза равнобедренного прямоугольного треугольника в 
раз больше катета. Получим:
|
|
|
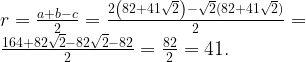
Ответ: 41.
Bписанные и описанные четырехугольники
27. B четырёхугольник ABCD вписана окружность,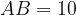 
, 
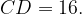Найдите периметр четырёхугольника ABCD.
B четырехугольник можно вписать окружность тогда и только тогда, когда суммы длин его противоположных сторон равны. Значит,
Тогда периметр четырехугольника равен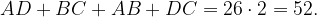 
28. Cтороны четырехугольника ABCD AB, BC, CD и AD стягивают дуги описанной окружности, градусные величины которых равны соответственно 95, 49, 71, 145 градусов. Найдите угол B этого четырехугольника. Ответ дайте в градусах.
Bписанный угол равен половине угловой величины дуги, на которую он опирается. Значит, угол B равен 
Ответ: 108.
C четырехугольником справились. A с n-угольником?
Угол между стороной правильного n-угольника, вписанного в окружность, и радиусом этой окружности, проведенным в одну из вершин стороны, равен 
Найдите n.
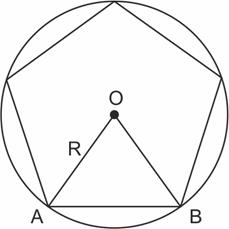
Рассмотрим треугольник AOB. Он равнобедренный, т. к. AO=OB=R. Значит,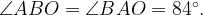 
Ответ: 30.
Задание 4
Есть в Профильном ЕГЭ по математике, и даже в первой его части, такие задачи, для решения которых можно знать ВСЁ. То есть всю школьную программу алгебры, с 5 класса до 11. Или почти всю.
Например, задание №4 Профильного ЕГЭ по математике – вычисления и преобразования. Вам могут встретиться и совсем простые задачи (на сложение дробей), и задания, которые не решить без подготовки. Например, вычисление и преобразование иррациональных выражений, тригонометрических, логарифмических. Задачи на определение модуля и понятие функции. В общем, типов задач здесь множество, по всему курсу алгебры.
И помните, что в ответе в заданиях первой части Профильного ЕГЭ по математике у вас должны получаться целые числа или конечные десятичные дроби.
|
|
|
