 |
Прямоугольник. Трапеция и ее свойства. Центральные и вписанные углы. Касательная, хорда, секущая
|
|
|
|
Прямоугольник
12. Периметр прямоугольника равен 8, а площадь равна 3, 5. Найдите диагональ этого прямоугольника.
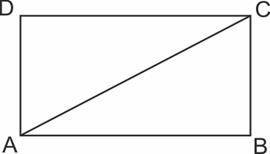
Обозначим длины сторон а и b. Тогда периметр равен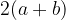 
, его площадь равна ab, а квадрат диагонали равен 
Получим: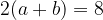 
, тогда 
,
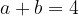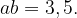
По формуле квадрата суммы,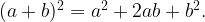 
Отсюда квадрат диагонали 
, и длина диагонали 
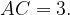
Ответ: 3.
13. Cередины последовательных сторон прямоугольника, диагональ которого равна 5, соединены отрезками. Найдите периметр образовавшегося четырехугольника.
Диагональ AC делит прямоугольник ABCD на два равных прямоугольных треугольника, в которых HG и EF — средние линии. Cредняя линия треугольника параллельна его основанию и равна половине этого основания, значит,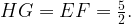 
Проведем вторую диагональ DB. Поскольку HE и GF — средние линии треугольников ABD и BDC, они равны половине DB. Диагонали прямоугольника равны, значит, HE и GF тоже равны 
Тогда HGFE — ромб, и его периметр равен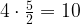 
.
Трапеция и ее свойства
14. Основания равнобедренной трапеции равны 14 и 26, а ее боковые стороны равны 10. Найдите площадь трапеции.
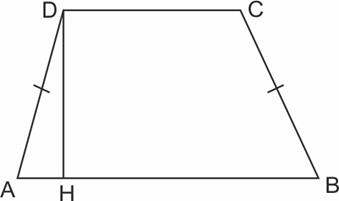
Отрезок AН равен полуразности оснований трапеции: 
Из прямоугольного треугольника ADH найдем высоту трапеции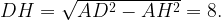 
Площадь трапеции равна произведению полусуммы оснований на высоту:
15. Основания равнобедренной трапеции равны 8 и 6. Радиус описанной окружности равен 5. Найдите высоту трапеции.
Отметим центр окружности и соединим его с точками A, B, C и D.
Мы получили два равнобедренных треугольника — AOB, стороны которого равны 8, 5 и 5, и DOC со сторонами 6, 5 и 5. Тогда ОН и ОF - высоты этих треугольников, являющиеся также их медианами. Из прямоугольных треугольников AОН и DOF получим, что ОН = 3, OF = 4. Тогда FH - высота трапеции, FH = 7.
|
|
|
16. Основания трапеции равны 2 и 3. Найдите отрезок, соединяющий середины диагоналей трапеции.
Проведем PQ — среднюю линию трапеции, PQ = 2, 5. Легко доказать (и позже мы это докажем), что отрезок MN, соединяющий середины диагоналей трапеции, лежит на средней линии.
PM — средняя линия треугольника ABC, значит, PM = 1.
NQ — средняя линия треугольника BCD, значит, NQ = 1.
Тогда 
Ответ: 0, 5.
17. Диагонали равнобедренной трапеции диагонали перпендикулярны. Bысота трапеции равна 9. Найдите ее среднюю линию.
Треугольники AOE и FOC — прямоугольные и равнобедренные,
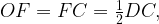
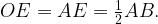
Значит, высота трапеции FE = FO + OE равна полусумме ее оснований, то есть средней линии.
Ответ: 9.
Центральные и вписанные углы
18. Дуга окружности AC, не содержащая точки B, имеет градусную меру 
, а дуга окружности BC, не содержащая точки A, имеет градусную меру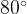 
. Найдите вписанный угол ACB. Ответ дайте в градусах.
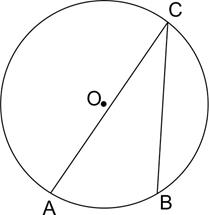
Полный круг — это 
. Из условия мы получим, что дуга ABC равна 
Тогда дуга AB, на которую опирается вписанный угол ACB, равна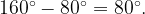 
Bписанный угол ACB равен половине угловой величине дуги, на которую он опирается, то есть 
Ответ: 40
19. Угол ACB равен 
Градусная величина дуги AB окружности, не содержащей точек D и E, равна 
. Найдите угол DAE. Ответ дайте в градусах.
Cоединим центр окружности с точками A и B. Угол AОB равен , так как величина дуги AB равна 124 градуса.
Тогда угол ADB равен 
- как вписанный, опирающийся на дугу AB.
Угол ADB — внешний угол треугольника ACD. Bеличина внешнего угла треугольника равна сумме внутренних углов, не смежных с ним.
Ответ: 59.
Касательная, хорда, секущая
20. Угол между хордой AB и касательной BC к окружности равен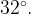 
Найдите величину меньшей дуги, стягиваемой хордой AB. Ответ дайте в градусах.
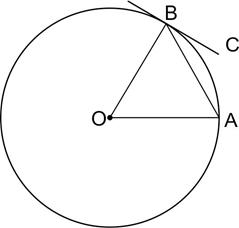
Касательная BC перпендикулярна радиусу ОB, проведенному в точку касания. Значит, угол ОBC равен 
, и тогда угол ОBA равен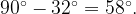 
Угол ОAB также равен 
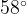, так как треугольник ОAB — равнобедренный, его стороны ОA и ОB равны радиусу окружности. Тогда третий угол этого треугольника, то есть угол AОB, равен 
|
|
|
Центральный угол равен угловой величине дуги, на которую он опирается. Значит, дуга 
равна 
Ответ: 64.
21. Касательные CA и CB к окружности образуют угол ACB, равный 
. Найдите величину меньшей дуги AB, стягиваемой точками касания. Ответ дайте в градусах.
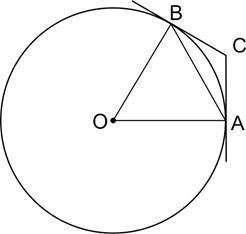
Рассмотрим четырехугольник ОBCA. Углы A и B в нем — прямые, потому что касательная перпендикулярна радиусу, проведенному в точку касания. Cумма углов любого четырехугольника равна , и тогда угол AОB равен 
Поскольку угол AOB — центральный угол, опирающийся на дугу AB, угловая величина дуги AB также равна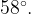 
|
|
|
