 |
Г.П. Хамитов, Т.И. Ведерникова
|
|
|
|
Г. П. Хамитов, Т. И. Ведерникова
1. ПРОСТРАНСТВО ЭЛЕМЕНТАРНЫХ СОБЫТИЙ. ОПЕРАЦИИ НАД СОБЫТИЯМИ
Основные понятия раздела
Исходом (элементарным событием) 
называется неразложимый результат испытания 
, характеризуемый значениями параметров, которые это испытание позволяют измерить.
Пространством 
исходов испытания называется множество 
всех исходов (элементарных событий), при этом пишут: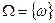 
, либо 
.
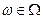Случайным событием называется свойство изучаемой системы, которое обнаруживается или не обнаруживается при каждой реализации испытания . Каждое событие 
характеризуется множеством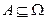 
тех точек , для которых оно имеет место. Событие определяется этим подмножеством и отождествляется с ним (событие произошло, если произошло какое-либо из элементарных событий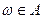 
).
Над множествами (событиями) можно выполнять элементарные операции теории множеств:
пересечение: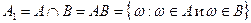 
, событие 
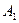– произведение событий и 
;
объединение: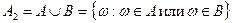 
, 
– сумма событий и .
Если пересечение компонент объединения представляет собой пустое множество, т. е.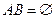 
(множество 
не содержит элементарных событий), то обозначают 
, а события и называют несовместимыми (несовместными).
Событие называют достоверным, событие – невозможным.
Разность событий и соответствует множеству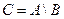 
, состоящему из элементарных исходов, принадлежащих и не принадлежащих . Событие 
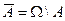называется дополнительным к (противоположным событию ).
Задачи с решениями
1. Монета подбрасывается три раза подряд. Под исходом опыта будем понимать последовательность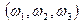 
, где каждый из 
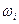обозначает выпадение " герба" или " решки". Требуется: а) построить пространство элементарных событий 
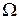; б) перечислить элементарные исходы, образующие случайное событие , состоящее в том, что выпало не менее двух " гербов".
|
|
|
Решение. Обозначим через Р выпадение " решки" и через Г – выпадение " герба", тогда каждое 
будет либо Р, либо Г.
а) 
.
б)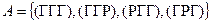 
.
2. Событие является частным случаем события (рис. 1. 1). Чему равны их объединение и произведение?
 |
Решение.
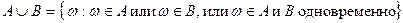. Из 
следует, что из осуществления события следует осуществление , т. е.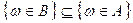 
. Отсюда можно записать, что 
. 
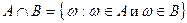. Исходя из того, что (т. е. если 
, то 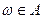), перепишем 
.
3. Даны два случайных события и .
а) Найти результаты операци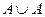й: 
и 
.
б) Когда события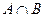 
и равносильны?
в) Являются ли совместными события и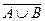 
?
Решение.
а)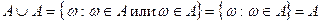 
.
.
б)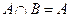 
, когда 
(см. задачу 2).
в)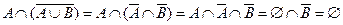 
. Следовательно, события и 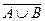несовместны.
4. Пусть , , 
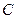– случайные события. Когда выполняются равенства:
а) 
; б)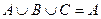 
?
Решение.
а) . Обозначим через 
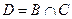и перепишем данное соотношение 
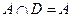. Отсюда видно (см. пример 2), что равенство имеет смысл, когда 
;
б)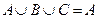 
, когда 
( 
).
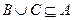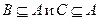5. Доказать, что события , 
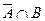и 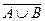образуют полную группу несовместных событий.
Решение. Случайные события образуют полную группу несовместных событий, если они попарно не пересекаются и в сумме образуют пространство исходов .
Имеем: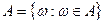 
, 
, 
. Отсюда получаем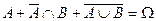 
. С другой стороны,
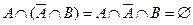, т. к. 
,
,
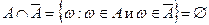Следовательно, события , 
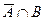и 
образуют полную группу несовместных событий.
6. Событие – хотя бы одно из имеющихся изделий бракованное; событие – бракованных изделий среди имеющихся четырех не менее двух. Что означают противоположные события: 
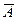и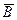 
?
Решение. Событие 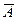является противоположным к событию A, следовательно, в сумме они образуют все пространство исходов, тогда 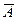означает, что среди имеющихся четырех изделий бракованных нет.
Рассуждая аналогично, утверждаем, что 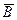означает – среди имеющихся четырех изделий бракованных меньше двух.
|
|
|
7. Отдел технического контроля проверяет изделия на стандартность. Пусть 
событие, состоящее в том, что i-ая деталь окажется стандартной. Выразить через 
событие, состоящее в том, что из трех проверенных изделий только одно нестандартное.
Решение. Обозначим через событие, состоящее в том, что из трех проверенных изделий только одно нестандартное. Возможно наступление трех несовместных событий: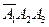 
– первое изделие нестандартно, а два другие стандартны; 
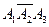– нестандартно только второе изделие; 
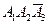– первые два изделия стандартны, третье нестандартно. Отсюда получаем, что 
.
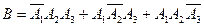8. В ящике содержатся шары двух цветов: синие и красные. Пусть 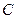– событие, состоящее в том, что при единичном испытании вынут синий шар, а 
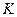– что при единичном испытании вынутый шар окажется красным. Запишите событие, означающее, что вынуты два шара одного цвета.
Решение. Обозначим искомое событие через . Оно будет заключаться в том, что вынуты или два синих шара, т. е. произошло событие 
, или два красных шара – событие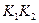 
. Эти два события являются несовместными, тогда получаем 
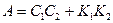(индексы означают номер испытания).
9. Среди студентов, собравшихся на лекцию, выбирают наудачу одного. Пусть событие заключается в том, что выбранный студент окажется юношей. Событие – в том, что студент не курит. Событие 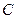состоит в том, что студент живет в общежитии.
а) В чем заключается смысл события 
?
б) При каком условии будет иметь место тождество ?
в) Когда будет справедливо соотношение 
?
г) Когда будет справедливо равенство 
?
Решение.
а) Событие – выбранный студент – юноша. Событие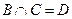 
– студент не курит и живет в общежитии. Событие 
является противоположным к событию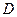 
, а это значит, что студент курит или не живет в общежитии (в терминах совместных событий), либо: курит и не живет в общежитии, или живет в общежитии и курит, или не курит и не живет в общежитии (в терминах несовместных событий). Тогда состоит в том, что выбран юноша, который не живет в общежитии или курит (в терминах совместных событий), либо: юноша курит и не живет в общежитии, или юноша живет в общежитии и курит, или юноша не курит и не живет в общежитии (в терминах несовместных событий). Формально: 
.
б) Воспользуемся обозначением 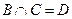и перепишем исходное равенство 
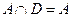. Тогда (см. пример 1) 
, т. е. тождество будет иметь место, когда все юноши не курят и живут в общежитии.
|
|
|
в) Событие 
означает, что студент не живет в общежитии, – что не курит. Соотношение будет справедливо тогда, когда неживущие в общежитии не курят.
г) Событие 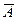означает, что выбрана девушка. Событие – студент не курит. Тогда справедливо, когда все девушки не курят, а все юноши курят.
10. Рабочий изготовил n деталей. Пусть событие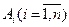 
заключается в том, что i-ая изготовленная им деталь имеет дефект. Записать событие, состоящее в том, что а) ни одна из деталей не имеет дефекта (событие ); б) хотя бы одна деталь имеет дефект; в) только одна деталь имеет дефект (событие ).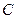
Решение.
а) Если есть событие, что i-ая изготовленная деталь имеет дефект, то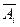 
– событие противоположное, т. е. i-ая деталь не имеет дефекта. Искомое событие состоит в том, что ни одна из n изготовленных деталей не имеет дефектов, т. е. и 1-ая деталь не имеет дефекта, и 2-ая деталь не имеет дефекта, и так далее, и n-ая деталь без дефекта, т. е. имеет место произведение событий 
.
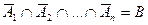б) Хотя бы одна деталь имеет дефект означает, что дефектными могут быть одна, две, ..., все детали, т. е. это событие является противоположным к событию B (п. (а) данной задачи). Искомое событие есть
.
в) Когда говорят, что только одна деталь имеет дефект, то это означает, что дефектна или 1-ая деталь, или 2-ая деталь, или и так далее n-ая деталь (при этом остальные (n-1) деталей не имеют дефектов). Тогда искомое событие запишется следующим образом:
.
|
|
|
