 |
2. Вероятности в дискретном пространстве исходов. Геометрические вероятности
|
|
|
|
2. ВЕРОЯТНОСТИ В ДИСКРЕТНОМ ПРОСТРАНСТВЕ ИСХОДОВ. ГЕОМЕТРИЧЕСКИЕ ВЕРОЯТНОСТИ
Основные понятия раздела
Пространство элементарных событий называется дискретным, если оно состоит из конечного или счетного числа точек.
Вероятность события есть численная мера степени объективной возможности этого события.
Пусть дано дискретное пространство элементарных событий 
и пусть с каждой точкой 
связано число, называемое вероятностью элементарного события и обозначаемое 
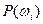, причём 
, 
. При этом говорят, что неотрицательная числовая функция 
задаёт на 
распределение вероятностей.
Вероятность 
события А есть сумма вероятностей тех элементарных исходов, которые образуют множество А, т. е. 
.
Говорят, что для испытания E с дискретным пространством построена вероятностная модель 
, если указаны все точки пространства элементарных событий 
и соответствующие вероятности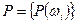 
исходов 
.
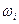Часто выделяют и рассматривают отдельно вероятностную модель с конечным пространством элементарных событий 
, когда 
для всех исходов 
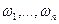испытания E. При этом исходы называют случаями (шансами) и говорят, что испытание E сведено к схеме случаев (схеме шансов), а вероятностную модель называют классической.
В рамках классической вероятностной модели вероятность случайного события А (классическое определение) вычисляется по формуле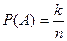 
, где n – число всех случаев, k – число случаев, благоприятствующих событию А.
Встречаются задачи, когда существует несчётное множество исходов. При этом, по-прежнему, основой послужит понятие " равновероятности" и " несовместности" некоторой " полной группы" элементарных событий. Пусть, например, на плоскости имеется область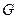 
, которая содержит другую область 
, имеющую своей границей замкнутую кривую. В область 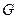наудачу бросается точка и спрашивается, чему равна вероятность того, что точка попадает в область . При этом выражению " точка бросается наудачу в область 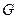" придаётся следующий смысл: брошенная точка может попасть в любую точку области 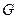, вероятность попасть в какую-либо часть области пропорциональна мере этой части (длине, площади и т. д. ) и не зависит от её расположения и формы. Здесь имеет место геометрическая вероятность – вероятность попадания в область , которая определяется как отношение мер: 
.
|
|
|
Задачи с решениями
1. В урне имеются 10 шаров: 3 белых и 7 черных. Из урны наугад вынимается 1 шар. Какова вероятность того, что этот шар: а) белый; б) черный.
Решение. В силу того, что число возможных способов достать шар из урны конечно и вероятность извлечения каждого шара одна и та же, применима классическая вероятностная модель.
а) Обозначим через A – событие, состоящее в том, что будет извлечен белый шар. Следовательно,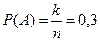 
, т. к. k=3 – число исходов, благоприятствующих событию A, а n=10 – число всех исходов пространства 
.
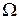б) Обозначив через B событие, состоящее в том, что из урны будет вынут черный шар, получим 
.
2. Из слова " НАУГАД" выбирается наугад одна буква.
а) Какова вероятность того, что эта буква " Я"?
б) Какова вероятность того, что это гласная?
Решение.
а) Обозначим через A событие, состоящее в том, будет выбрана буква " Я". Число возможных способов выбрать одну букву из заданного слова n=6 (количество букв в слове). Применим классическое определение вероятности. Число благоприятных исходов 
. Тогда вероятность искомого события 
.
б) Обозначим через B событие, заключающееся в выборе гласной буквы. Число гласных букв в слове есть число исходов, благоприятных событию B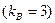 
. Отсюда получаем 
.
|
|
|
3. Брошены три монеты. Найти вероятность того, что выпадут два " герба"?
Решение. Элементарный исход испытания представляет собой последовательность 
, где каждый из 
обозначает выпадение " герба" (Г) или " решки" (Р). Обозначим через 
событие, состоящее в том, что выпадут два " герба", и перечислим все исходы этого события:
.
Пространство исходов устроено следующим образом
.
Применив классическое определение вероятности, получаем
.
4. В урне 4 красных и 6 черных шаров. Наугад вынимается 3 шара. Какова вероятность, что два шара будут черного цвета?
Решение. Обозначим через A событие, состоящее в том, среди вынутых трех шаров два будут черного цвета. Так как число исходов конечно и все исходы равновероятны, можно применить классическую вероятностную модель, согласно которой вероятность искомого события есть 
.
Элементарный исход испытания представляет собой выбор трех любых шаров. Число n всех исходов испытания представляет собой множество способов вынуть 3 шара из 10. Это есть число сочетаний из 10 по 3, т. е. 
. Число благоприятных исходов составляют лишь те, когда среди трех шаров есть два черных и один красный. Другими словами можно сказать, что здесь как бы составляются пары из одного красного и двух черных шаров. Количество способов взять 1 красный шар из 4 есть 
, а 2 черных шара из 6 есть 
, отсюда получаем число возможных пар 
. Тогда окончательно
.
5. При наборе телефонного номера абонент забыл две последние цифры и набрал их наудачу, помня только, что эти цифры нечетные и разные. Найти вероятность того, что номер набран правильно.
Решение. Обозначим через A искомое событие и применим для вычисления классическую вероятностную модель. Под исходом испытания будем понимать набор двух любых разных цифр от 0 до 9. Причем исходы, когда две цифры переставлены местами будем считать различными. Такое комбинаторное многообразие отвечает размещению из 10 элементов по 2, т. е.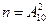 
. Благоприятных исходов 1. Тогда получаем, что
.
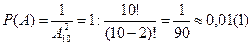6. A и B и еще 8 человек стоят в очереди. Определить вероятность того, что A и B отделены друг от друга тремя персонами.
Решение. Пусть D – событие, состоящее в том, что A и B отделены друг от друга тремя лицами. Для определения вероятности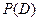 
можно применить классическое определение, т. к. пространство исходов конечно и все исходы равновероятны. Исход испытания в данной задаче представляет собой любую последовательность людей в очереди из 10 человек. Число способов переставить этих людей есть 
. Количество благоприятных исходов будет образовываться " парами" 
, 
; 
, 
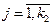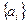– способы расположения A и B так, чтобы их отделяло 3 человека 
, 
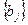– это всевозможные перестановки оставшихся 8 человек очереди 
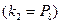. Окончательно получаем:
|
|
|
.
7. В партии из 50 изделий 5 бракованных. Из партии наугад выбираются 6 изделий. Определить вероятность того, что среди этих 6 изделий 2 окажутся бракованными.
Решение. Обозначим через A событие, состоящее в том, что среди 6 выбранных наугад изделий 2 окажутся бракованными и для нахождения вероятности применим классическую вероятностную модель. Элементарный исход испытания в данной задаче заключается в выборе произвольным образом 6 изделий из 50, и количество всех исходов определяется как число сочетаний из 50 по 6, т. е. 
. Число исходов, благоприятных событию A, составляют лишь те из n, когда присутствуют 2 бракованных. Таким образом, в каждой шестерке присутствуют 2 бракованных изделия и 4 небракованных, т. е. как бы составляются пары из бракованных и небракованных изделий, причем одна шестерка отличается от другой, если они различаются хотя бы одним элементом. Число способов выбрать 2 бракованных изделия есть 
, а число способов выбрать 4 небракованных – это 
. Тогда
.
8. Найти вероятность того, что дни рождения 12 человек придутся на разные месяцы года.
Решение. Пусть A – событие, состоящее в том, что дни рождения всех 12 человек придутся на разные месяцы года. Исход испытания представляет собой один из способов распределения по месяцам дней рождения 12 человек, причем все 12 могут родиться и в один месяц, т. е. образование исходов аналогично выбору с возвращением 
элементов из совокупности равной 
. Тогда число всех элементарных событий 
, а число исходов благоприятных искомому событию 
(в каждый месяц только один день рождения, но для разных людей они могут быть переставлены внутри года). Окончательно получаем:
|
|
|
.
9. В лифт семиэтажного дома на первом этаже вошли 3 человека. Каждый из них с одинаковой вероятностью выходит на любом из этажей, начиная со второго. Найти вероятность следующих событий:
а) 
;
б) 
;
в) 
.
Решение. Элементарное событие в данной задаче заключается в том, что хотя бы на одном этаже, начиная со второго, выйдет хотя бы один человек, что представляет собой выбор каждым из трех человек одного из шести этажей (троекратный выбор наугад с возвращением одного из шести элементов), т. е.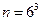 
.
а) Событию A благоприятствует только один исход, тогда
.
б) Событие B представляет собой сумму из 6-ти событий, аналогичных событию ( 
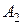– все выйдут на втором этаже, 
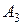– все выйдут на третьем этаже и т. д., 
– все выйдут на седьмом этаже).
,
где все 
, 
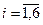по условию. Отсюда 
.
в) Число исходов, благоприятствующих событию C, представляет собой число сочетаний из 6 элементов по 3, т. е.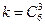 
. Тогда
.
10. На отрезок наудачу брошены две точки. Найти вероятность того, что расстояние между ними окажется меньше половины.
Решение. Обозначим через L – длину заданного отрезка, через l – расстояние между точками, а через A – событие, состоящее в том, что 
. Так как число точек на отрезке (и на любой его части) бесконечно, применим для нахождения геометрическое определение вероятности: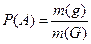 
, где 
есть мера пространства исходов, а 
– мера исходов, благоприятных событию A.
Пусть x – координата первой точки, а y – координата второй точки, тогда событию A будут удовлетворять исходы, отвечающие условию 
или 
, что соответствует заштрихованной области на рис. 2. 1. Тогда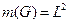 
, а 
и 
.
 |
|
|
|
