 |
3. Условная вероятность. Независимость событий и испытаний. Теоремы сложения и умножения вероятностей
|
|
|
|
3. УСЛОВНАЯ ВЕРОЯТНОСТЬ. НЕЗАВИСИМОСТЬ СОБЫТИЙ И ИСПЫТАНИЙ. ТЕОРЕМЫ СЛОЖЕНИЯ И УМНОЖЕНИЯ ВЕРОЯТНОСТЕЙ
Основные понятия и теоремы раздела
Вероятность 
события A, вычисленная при условии, что имело место другое событие B, называется условной вероятностью события A при условии B. Для произвольных событий A и B условная вероятность
, если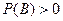 
.
Теорема (сложения вероятностей). Для любых двух событий A и B вероятность того, что имеет место либо событие A, либо событие B, либо оба эти события (объединение событий A и B), задаётся формулой:
.
Теорема (умножения вероятностей). Вероятность совместного наступления двух событий равна произведению вероятности одного из них на условную вероятность другого при условии, что первое наступило:
.
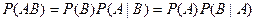События A и B называются независимыми, если имеет место равенство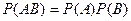 
.
События 
называются независимыми в совокупности, если для любых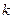 
из них ( 
) выполняется соотношение
.
Если это соотношение выполняется только при 
, то события называются попарно независимыми.
Задачи с решениями
1. В ящике 10 красных и 6 синих шаров. Вынимаются наудачу 2 шара. Какова вероятность того, что они будут одноцветными?
Решение. Пусть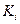 
– событие, состоящее в том, что при i-ом испытании 
вынут красный шар, 
– вынут синий шар, а A – что вынуты два шара одного цвета. Тогда справедливо: 
. Применив теорему сложения вероятностей для несовместных событий, имеем
.
Далее можно использовать классическое определение для нахождения вероятностей 
и 
.
.
2. Найти вероятность того, что наудачу взятое двузначное число окажется кратным либо 2, либо 5, либо тому и другому одновременно.
Решение. Событие A – число кратно 2; B – кратно 5;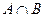 
– кратно 2 и 5 одновременно. Тогда
|
|
|
.
3. В одном ящике 5 белых и 10 красных шаров, в другом – 20 белых и 5 красных шаров. Найти вероятность того, что хотя бы из одного ящика будет вынут белый шар, если из каждого ящика вынуто по одному шару.
Решение. Пусть A – событие, состоящее в том, что хотя бы из одного ящика вынут белый шар,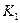 
и 
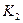– независимые события, означающие, что из первого и второго ящика соответственно вынуты красные шары. Тогда событие A представляется следующим образом: 
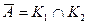. Отсюда находим
.
Примечание. Следует обратить внимание на технологический прием в решении этой и ряда последующих задач, заключающийся в том, что искомый результат находится проще в терминах противоположных событий.
4. Вероятность того, что в течение одной смены возникнет неполадка станка, равна 0, 05. События эти независимы. Какова вероятность того, что а) не произойдут неполадки за три смены; б) неполадка произойдет только в одной смене?
Решение. Пусть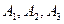 
– независимые события, состоящие в том, что произойдет неполадка станка в первую, во вторую, в третью смену соответственно, причем 
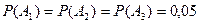. Вероятности противоположных событий равны 
.
а) Обозначим через 
событие, состоящее в том, что за все три смены не произойдут неполадки. Это событие можно представить следующим образом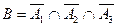 
. Отсюда, используя теорему умножения вероятностей и независимость событий, получаем
.
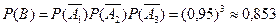б) Пусть C означает событие, что неполадка произойдет только в одну из трех смен. Это событие записывается следующим образом
.
Далее на основании теорем сложения и умножения вероятностей, находим вероятность события C:
5. Бросается симметричная монета до первого появления " герба" (в схеме независимых испытаний). Описать пространство элементарных событий. Найти вероятность того, что потребуется четное число бросков.
Решение. Пусть Г – выпадение " герба" и Р – выпадение " решки". Тогда пространство элементарных событий представляет собой счетное число исходов и описывается следующим образом: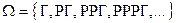 
.
|
|
|
Обозначим через 
– событие, состоящее в том, что потребуется четное число бросков. Это событие включает в себя каждый второй исход из 
, т. е.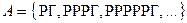 
. Отсюда, учитывая независимость выпадения " герба" и " решки", и, что 
, находим, что
.
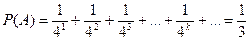Примечание. Поучительный пример для тех, кто, полагаясь на интуицию, считает, что " на равных" можно играть, ставя на четное или нечетное число бросков.
6. Предположим, что вероятность потопить корабль одной торпедой равна 0, 6. Какова вероятность того, что 4 торпеды потопят корабль? Для потопления достаточно одной торпеды, причем " испытания торпедами" независимы.
Решение. Пусть A – событие, означающее, что корабль будет потоплен. Противоположное событие можно представить как произведение независимых событий: 
, где 
состоит в том, что i-ая торпеда не потопит корабль. Применяя теорему умножения для независимых событий, получим искомую вероятность:
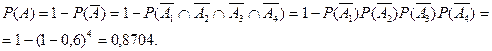
7. В ящике лежат 12 красных, 8 зеленых и 10 синих шаров. Наудачу вынимаются два шара. Какова вероятность, что вынутые шары разного цвета, если известно, что вынут синий шар?
Решение. Введем обозначения: A – событие, состоящее в том, что вынуты два шара разного цвета, если известно, что вынут синий шар; K – вынут красный шар; C – вынут синий шар; Z – вынут зеленый шар (события K, C и Z являются независимыми). Отсюда имеем: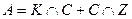 
. Тогда 
. Далее получаем
.
8. Имеются четыре бракованных изделия: на одном повреждена краска (событие А), на другом имеется вмятина (событие В), на третьем – зазубрины (событие С), а на четвертом – одновременно все три указанных дефекта. Являются ли данные события независимыми попарно и в совокупности?
Решение. Так как каждый из трех дефектов имеется у двух изделий, то 
. Любая пара дефектов присутствует только у одного изделия, поэтому вероятность пересечения событий 
. Это означает попарную независимость всех трех событий. С другой стороны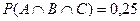 
, а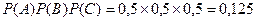 
, т. е. события А, В и С не являются независимыми в совокупности.
9. Бросается симметричная игральная кость. Какова вероятность того, что выпадет простое число очков (событий A), если известно, что число выпавших очков нечетно (событие B).
|
|
|
Решение. Ясно, что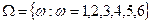 
, 
, 
. Тогда 
. Отсюда, применяя формулу условной вероят-ности, находим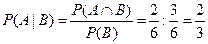 
.
10. Бросаются 4 игральные кости. Найти вероятность того, что на них выпадет по одинаковому числу очков.
Решение. Обозначим через B – событие, состоящее в том, что на всех гранях четырех игральных костей выпадет одинаковое число очков. Пусть 
означает, что на грани i-ой кости выпадет 1, 
означает, что выпадет 2 и так далее, 
означает, что на грани i-ой кости выпадет 6. Событие B можно записать как сумму произведений независимых событий: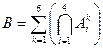 
. Вероятность 
легко находится использованием теорем сложения и умножения вероятностей: 
.
|
|
|
