 |
Задачи для самостоятельной работы
|
|
|
|
1. 1. Бросается игральная кость. Событие  – выпадет четное число очков, событие
– выпадет четное число очков, событие  – выпадет число очков, меньшее трех. Что означают следующие события:
– выпадет число очков, меньшее трех. Что означают следующие события:  ,
, 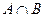 ,
,  ,
, 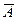 ,
, 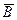 ?
?
1. 2. Бросаются две игральные кости. Событие  – на каждой грани выпадает четное число очков, событие
– на каждой грани выпадает четное число очков, событие  – на каждой грани выпадает нечетное число очков, событие
– на каждой грани выпадает нечетное число очков, событие 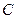 – хотя бы на одной из костей выпала 1, событие
– хотя бы на одной из костей выпала 1, событие 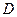 – сумма очков на верхних гранях четная,
– сумма очков на верхних гранях четная,  – на каждой грани выпадут очки одной четности.
– на каждой грани выпадут очки одной четности.
а) Что означают события:  ,
, 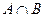 ,
,  ,
,  ,
, 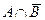 ,
,  ,
, 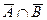 ,
, 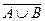 и
и  ?
?
б) Доказать, что  .
.
в) Описать события:  ,
, 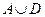 ,
,  ,
,  ,
,  ,
,  .
.
1. 3. Пусть  ,
,  и
и 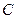 – три произвольных события. Найти выражения для событий, состоящих в том, что из
– три произвольных события. Найти выражения для событий, состоящих в том, что из  ,
,  и
и 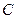 : а) произошли все три события; б) произошло только одно из этих событий; в) произошло, по крайней мере, два из этих событий.
: а) произошли все три события; б) произошло только одно из этих событий; в) произошло, по крайней мере, два из этих событий.
1. 4. Объединение  двух событий может быть выражено как объединение двух несовместных событий
двух событий может быть выражено как объединение двух несовместных событий  . Выразить аналогичным образом объединение трех событий
. Выразить аналогичным образом объединение трех событий  ,
,  и
и 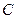 .
.
1. 5. Доказать равенство  . Изобразить фигурами на плоскости множества, стоящие в левой и правой частях доказываемого равенства.
. Изобразить фигурами на плоскости множества, стоящие в левой и правой частях доказываемого равенства.
1. 6. Доказать равенство  . Изобразить фигурами на плоскости множества, стоящие в левой и правой частях доказываемого равенства.
. Изобразить фигурами на плоскости множества, стоящие в левой и правой частях доказываемого равенства.
1. 7. Пусть заданы два произвольных случайных события  и
и  . Найти все события
. Найти все события 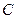 такие, что
такие, что 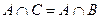 .
.
1. 8. Доказать равенство  .
.
1. 9. Двое играют в шахматы. Событие  означает, что выиграл первый игрок, событие
означает, что выиграл первый игрок, событие  – выиграл второй игрок. Что означают события:
– выиграл второй игрок. Что означают события:  ,
,  ,
, 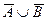 ,
,  ,
, 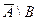 и
и 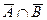 ?
?
1. 10. Из урны, содержащей черные и белые шары, извлечены 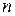 шаров. Пусть
шаров. Пусть  – событие, состоящее в том, что i-ый шар белый (
– событие, состоящее в том, что i-ый шар белый (  ). Выразить через
). Выразить через  следующие события: а) все извлеченные шары окажутся одного цвета; б) среди вынутых шаров есть хотя бы один белый; в) среди n извлеченных шаров только один шар белый; г) среди извлеченных шаров не более k шаров белого цвета (
следующие события: а) все извлеченные шары окажутся одного цвета; б) среди вынутых шаров есть хотя бы один белый; в) среди n извлеченных шаров только один шар белый; г) среди извлеченных шаров не более k шаров белого цвета ( 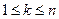 ); д) среди вынутых шаров, по крайней мере, k шаров белые; е) среди n шаров ровно k белых.
); д) среди вынутых шаров, по крайней мере, k шаров белые; е) среди n шаров ровно k белых.
|
|
|
1. 11. Одновременно бросаются три монеты. Событие  – выпадет хотя бы одна " решка", событие
– выпадет хотя бы одна " решка", событие  – выпадет хотя бы один " герб". Что означают события
– выпадет хотя бы один " герб". Что означают события  ,
, 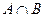 и
и  ?
?
1. 12. Из множества супружеских пар наугад выбирается одна пара. Событие A состоит в том, что мужу больше 30-ти лет, событие B – муж старше жены, событие C – жене больше 30 лет. Что означают события:  ,
,  ,
,  ,
, 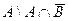 ,
, 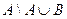 и
и 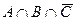 ?
?
1. 13. Событие  заключается в том, что при i-ом измерении некоторой физической величины допущена ошибка. Произведены три независимых измерения. Записать через
заключается в том, что при i-ом измерении некоторой физической величины допущена ошибка. Произведены три независимых измерения. Записать через  событие, состоящее в том, что только в одном из них допущена ошибка.
событие, состоящее в том, что только в одном из них допущена ошибка.
1. 14. В отдел технического контроля поступило N приборов. Событие  состоит в том, что i-ый прибор является неисправным. Записать через
состоит в том, что i-ый прибор является неисправным. Записать через  событие, означающее, что среди N поступивших приборов неисправных нет.
событие, означающее, что среди N поступивших приборов неисправных нет.
1. 15. Пусть A, B и C – произвольные события, причем 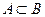 . Упростить выражения: а)
. Упростить выражения: а) 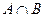 ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
1. 16. Каково условие совместности событий:  ,
,  и
и  ?
?
1. 17. Мишень состоит из десяти кругов, ограниченных концентрическими окружностями с радиусами  . Событие
. Событие  – попадание в круг радиуса
– попадание в круг радиуса  . Что означают события: а)
. Что означают события: а)  ; б)
; б)  ; в)
; в) 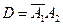 .
.
1. 18. Пусть A и B – произвольные события. Доказать следующие равенства: а)  ; б)
; б) 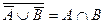 .
.
1. 19. Пусть на плоскость, на которой изображены два непересекающихся круга, бросается точка. Событие A – точка попадает в первый круг, событие B – точка попадает во второй круг. Что означают события: 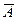 ,
, 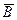 ,
,  ,
, 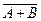 ,
,  ,
, 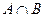 ,
,  ?
?
1. 20. Проводятся три независимых испытания, в каждом из которых некоторое событие может появиться (  ) или не появиться (
) или не появиться ( 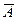 ). Выразить через
). Выразить через  и
и 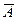 следующие события: а) событие произошло в первом испытании; б) событие произошло два раза; в) событие произошло не более двух раз.
следующие события: а) событие произошло в первом испытании; б) событие произошло два раза; в) событие произошло не более двух раз.
|
|
|
1. 21. Два лица A и B условились встретиться в определенном месте между 12 и 13 часами. Пришедший первым ждет другого в течение 20 минут, после чего уходит. Изобразить фигурами на плоскости пространство  всех исходов и подпространство
всех исходов и подпространство  исходов, благоприятствующих встрече, если приход A и B в течение указанного часа происходит " наудачу".
исходов, благоприятствующих встрече, если приход A и B в течение указанного часа происходит " наудачу".
1. 22. Плоскость разграфлена параллельными прямыми, отстоящими друг от друга на расстоянии 2a. На плоскость наудачу бросается игла длины  . Событие A заключается в том, что игла пересечет какую-нибудь прямую. Изобразить на плоскости событие A и пространство
. Событие A заключается в том, что игла пересечет какую-нибудь прямую. Изобразить на плоскости событие A и пространство  .
.
1. 23. Доказать, что  .
.
1. 24. Задано двухзначное число. Событие A – число делится на 2, событие B – число делится на 5. Объяснить смысл событий:  ,
, 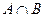 ,
, 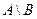 ,
, 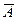 ,
, 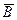 ,
,  ,
,  ?
?
1. 25. Доказать, что событие  невозможно.
невозможно.
1. 26. Три шара a, b и c размещаются по трем ящикам. Перечислить все возможные исходы испытания.
1. 27. Четыре одинаковых шара размещаются по четырем ящикам. Перечислить все возможные исходы испытания. Выделить событие, когда два ящика остаются свободными.
1. 28. Три игрока a, b и c участвуют в игре по следующей схеме. В первом туре играют а и b, игрок с свободен. Проигравший заменяется игроком с, во втором туре играют победитель и игрок с. Игрок, потерпевший поражение в первом туре, – свободен. В третьем туре играют победитель второго тура и игрок, проигравший в первом туре. Соревнование продолжается таким образом до тех пор, пока один из игроков не выиграет двух партий подряд. В этом случае его объявляют победителем. Перечислить все возможные исходы испытания (возможность ничьей в отдельной партии исключается).
1. 29. Пусть  состоит из
состоит из  точек
точек  , где координаты
, где координаты 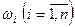 принимают значения
принимают значения  или
или  . Пусть
. Пусть  ,
, 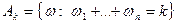 ;
; 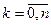 и
и  – число точек
– число точек  , входящих в
, входящих в  . Показать, что
. Показать, что 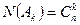 .
.
1. 30. Пусть имеется урна с  различными шарами, отличающимися один от другого тем, что они пронумерованы числами
различными шарами, отличающимися один от другого тем, что они пронумерованы числами  . Предположим, что
. Предположим, что 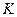 из этих шаров – красные и
из этих шаров – красные и  – чёрные. После каждого извлечения из урны шар возвращается обратно. Тогда результат m извлечений можно записать в виде:
– чёрные. После каждого извлечения из урны шар возвращается обратно. Тогда результат m извлечений можно записать в виде: 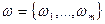 , где каждое из
, где каждое из  принимает одно из
принимает одно из  значений. Следовательно, множество
значений. Следовательно, множество  будет состоять из
будет состоять из 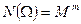 элементарных исходов. Пусть
элементарных исходов. Пусть  – событие, состоящее в том, что среди вынутых шаров ровно
– событие, состоящее в том, что среди вынутых шаров ровно 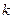 – красного цвета и
– красного цвета и 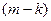 – чёрного. Показать, что
– чёрного. Показать, что 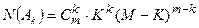 .
.
|
|
|
1. 31. Предположим, что есть m различных шаров, из которых 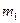 – первого цвета, ... ,
– первого цвета, ... , 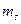 – s-го цвета (
– s-го цвета (  ). Будем рассматривать выбор с возвращением и обозначать результат n извлечений
). Будем рассматривать выбор с возвращением и обозначать результат n извлечений  . Тогда
. Тогда  . Обозначим
. Обозначим  множество тех
множество тех  , у которых
, у которых  координат первого цвета и т. д.,
координат первого цвета и т. д., 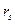 координат s-го цвета (
координат s-го цвета ( 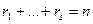 ). Показать, что
). Показать, что  .
.
1. 32. В условиях задачи 1. 30 предположим, что после каждого извлечения вынутый шар в урну не возвращается. Тогда результат m таких извлечений можно представить в виде: 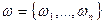 ;
;  . Пусть
. Пусть 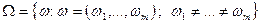 . Тогда
. Тогда  , где
, где
 .
.
По-прежнему событие  состоит в том, что среди вынутых шаров ровно
состоит в том, что среди вынутых шаров ровно 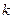 – красного цвета и
– красного цвета и 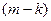 – чёрного. Показать, что
– чёрного. Показать, что 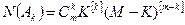
|
|
|


