 |
4. Формула полной вероятности. Формула Байеса
|
|
|
|
4. ФОРМУЛА ПОЛНОЙ ВЕРОЯТНОСТИ. ФОРМУЛА БАЙЕСА
Основные понятия и теоремы раздела
Пусть пространство элементарных событий 
вероятностной модели 
представляется в виде суммы
; 
, 
(*)
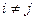попарно непересекающихся событий (гипотез) 
; 
(на языке классической теории вероятностей эти события называют полной группой несовместных событий).
Теорема (о полной вероятности). Если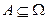 
и имеет место (*), то
.
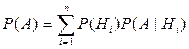Теорема Байеса. Если 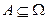и имеет место (*), то
; 
.
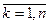Задачи с решениями
1. В урне содержится 4 шара белого и черного цветов. К ним прибавляют 2 белых шара. После этого из урны случайным образом вынимают 3 шара. Найти вероятность того, что все вынутые шары белые, считая равновозможными все предположения о первоначальном содержании урны.
Решение. Пусть A – событие, состоящее в том, что вынуты 3 белых шара. Предположения о равновозможном содержании белых и черных шаров в первоначальном составе урны являются гипотезами: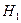 
– в урне все шары белые; 
– в урне 1 шар черный и 3 белых; 
– в урне 2 черных и 2 белых шара; 
– в урне 3 черных и 1 белый шар;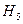 
– все шары в урне черные. События 
отвечают определению полной группы несовместных событий. Применим для нахождения вероятности 
формулу полной вероятности: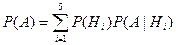 
, где
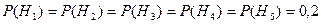и
, 
, 
, 
, 
.
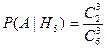Отсюда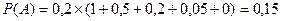 
.
2. В одной урне 5 белых и 6 черных шаров, а в другой – 4 белых и 8 черных шаров. Из первой урны случайным образом вынимают 3 шара и опускают во вторую урну. После этого из второй урны также случайно вынимают 4 шара. Найти вероятность того, что все шары, вынутые из второй урны, белые.
Решение. Обозначим через A событие, состоящее в том, что все шары, вынутые из второй урны, белые. Вероятность события A зависит от того, какого цвета будут 3 шара, которые переложены из первой урны во вторую. Здесь возможны следующие гипотезы: 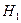– все шары белые; – 1 шар черный и 2 белые; – 2 шара черных и 1 белый; – все шары черные. События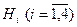 
образуют полную группу несовместных событий на том же пространстве исходов, где имеет место событие A, следовательно, для нахождения можно применить формулу полной вероятности. Здесь
|
|
|
;
.
.
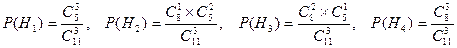3. В пирамиде стоят 19 винтовок, из них 3 с оптическим прицелом. Стрелок, стреляя из винтовки с оптическим прицелом, может поразить мишень с вероятностью 0, 81, а стреляя из винтовки без оптического прицела, – с вероятностью 0, 46. Найти вероятность того, что стрелок поразит мишень, стреляя из случайно взятой винтовки.
Решение. Пусть A означает событие, состоящее в том, что стрелок поразит мишень, стреляя из случайно взятой винтовки. 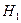– стрелок возьмет винтовку с оптическим прицелом; 
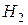– стрелок возьмет винтовку без оптического прицела. Тогда, применяя формулу полной вероятности, имеем:
.
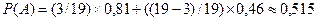4. В монтажном цехе к устройству присоединяется электродвигатель. Электродвигатели поставляются тремя заводами-изготовителями. На складе имеются электродвигатели названных заводов в количестве 19, 6 и 11 штук соответственно, которые могут безотказно работать до конца гарантийного срока с вероятностями 0, 85, 0, 76 и 0, 71 соответственно. Рабочий берет наугад один двигатель и монтирует его к устройству. Найти вероятности того, что смонтированный и работающий безотказно до конца гарантийного срока электродвигатель поставлен а) первым, б) вторым, в) третьим заводом-изготовителем.
Решение. Пусть A – событие, состоящее в том, что наугад взятый и присоединенный к устройству двигатель, будет работать безотказно до конца гарантийного срока; 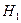– гипотеза, означающая, что двигатель изготовлен первым заводом; – двигатель изготовлен вторым заводом; – изготовлен третьим заводом. В данной задаче предполагается, что событие A произошло, необходимо только установить, какая гипотеза имела при этом место? Для этого нужно использовать формулу Байеса:
|
|
|
,
– определяется по формуле полной вероятности.
, 
, 
.
, 
, 
.
.
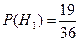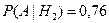а) 
;
б)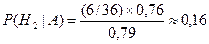 
;
в) 
.
5. Из 18 стрелков 5 попадают в мишень с вероятностью 0, 8; 7 – с вероятностью 0, 7; 4 – с вероятностью 0, 6 и 2 – с вероятностью 0, 5. Наудачу выбранный стрелок произвел выстрел и поразил мишень. К какой из групп вероятнее всего принадлежал стрелок?
Решение. Чтобы ответить на поставленный вопрос, необходимо определить условные вероятности 
попадания в мишень стрелками каждой из четырех групп (гипотез). Стрелок будет принадлежать к той группе, чья вероятность будет выше.
.
; 
;
; 
.
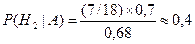Вероятнее всего выстрел произвел стрелок из второй группы, в которой вероятность попадания в мишень равна 0, 7 (хотя, быть может, кому-то показалось, что выстрел произвел стрелок из первой группы, так как вероятность поражения мишени стрелком этой группы равна 0, 8).
6. Предположим, что 5% всех мужчин и 0, 25% всех женщин дальтоники. Наугад выбранное лицо страдает дальтонизмом. Какова вероятность того, что это мужчина? (Считать, что мужчин и женщин одинаковое число).
Решение. В предположении о том, что число мужчин и женщин одинаково, вероятности гипотез ( 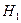– выбран мужчина, – выбрана женщина) равны между собой и равны 0, 5. Тогда, применяя формулу Байеса, находим вероятность того, что это мужчина:
.
7. Изделие проверяется на стандартность одним из двух товароведов. Вероятность того, что изделие попадет к первому товароведу, равна 0, 55, а ко второму – 0, 45. Вероятность того, что изделие будет признано стандартным для первого товароведа, равна 0, 9, а для второго – 0, 98. При проверке изделие было признано стандартным. Найти вероятность того, что это изделие проверил второй товаровед.
Решение. Событие A, состоящее в том, что изделие стандартно, свершилось. Необходимо найти вероятность того, это изделие проверил второй товаровед. Применим формулу Байеса.
.
8. В специализированную больницу поступают в среднем 50% больных с заболеванием K, 30% – с заболеванием L и 20% – с заболеванием M. Вероятность полного излечения болезни K равна 0, 7; для болезней L и M вероятности соответственно равны 0, 8 и 0, 9. Больной, поступивший в больницу, был выписан здоровым. Найти вероятность того, что этот больной страдал заболеванием K.
|
|
|
Решение. Обозначим через A событие, заключающееся в том, что больной выздоровел, а через K, L и M то, что он страдал одним из трех заболеваний. Для определения искомой вероятности применим формулу Байеса.
.
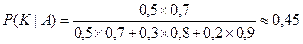9. Число грузовых автомашин, проезжающих по шоссе, на котором стоит бензоколонка, относится к числу легковых автомашин, проезжающих по тому же шоссе, как 3: 2. Вероятность того, что будет заправляться грузовая машина, равна 0, 1; для легковой машины эта вероятность равна 0, 2. К бензоколонке подъехала машина. Найти вероятность того, что это грузовая машина.
Решение. Так как соотношение грузовых и легковых машин составляет 3: 2, обозначим число грузовых за 3n, а число легковых за 2n машин. Пусть A – событие, означающее, что машина подъехала к бензоколонке, 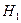и – гипотезы, означающие, что это грузовая или легковая машины соответственно. Искомую вероятность находим по формуле:
.
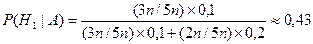10. Вероятность того, что во время работы ЭВМ произойдет сбой в арифметическом устройстве (АУ), в оперативной памяти (ОП), в остальных устройствах (ОУ), относятся как 3: 2: 5. Вероятности обнаружения сбоя в АУ, ОП и в ОУ соответственно равны 0, 8, 0, 9 и 0, 9. Найти вероятность того, что возникший в машине сбой будет обнаружен.
Решение. Пусть A – событие, означающее, что сбой будет обнаружен; 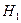– сбой был в АУ; – сбой в ОП; – сбой в ОУ. Обозначим вероятности гипотез через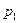 
, 
и 
соответственно. Найдем эти вероятности, используя их отношения: 
, 
, 
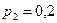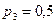. Для определения применим формулу полной вероятности, тогда
.
|
|
|
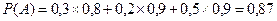