Задачи для самостоятельной работы

3. 1. В электрическую цепь последовательно включены 3 элемента, работающие независимо один от другого. Вероятность отказов первого, второго и третьего элементов соответственно равны 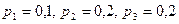. Найти вероятность того, что тока в цепи не будет.

3. 2. Сформулировать и доказать теоремы сложения и умножения вероятностей для любых трех событий A, B и C.

3. 3. Студент пришел на зачет, зная из 30 вопросов только 24. Какова вероятность сдать зачет, если для этого необходимо ответь на первый попавшийся вопрос или после отказа отвечать на первый вопрос ответить на пять следующих вопросов подряд?

3. 4. Гардеробщица выдала одновременно номерки шести лицам, сдавшим в гардероб свои шляпы. После этого она перепутала все шляпы и повесила их наугад. Найти вероятности следующих событий: а) каждому из шести лиц гардеробщица выдаст его собственную шляпу; б) ровно три лица получат свои шляпы; в) ровно два лица получат свои шляпы; г) только одно лицо получит свою шляпу; д) ни одно из шести лиц не получит своей шляпы.

3. 5. Разыскивая специальную книгу, студент решил обойти 3 библиотеки. Для всех библиотек одинаково вероятно: в настоящее время искомая книга есть в ее фондах 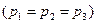; книга на руках . Что более вероятно – достанет студент книгу или нет, если известно, что библиотеки комплектуются независимо одна от другой?

3. 6. В ящике 8 зеленых и 12 синих шаров. Наудачу вынимаются 3 шара. Какова вероятность того, что они будут одного цвета?

3. 7. Отдел технического контроля проверяет изделия на стандартность. Вероятность того, что изделие нестандартно, равна 0, 1. Найти вероятность того, что а) из трех проверенных изделий только одно окажется нестандартным; б) нестандартным окажется четвертое по порядку проверяемое изделие.

3. 8. Два стрелка независимо друг от друга стреляют по мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0, 7, для второго – 0, 8. Найти вероятность того, что при одном выстреле каждым стрелком а) цель будет поражена; б) в цель попадут оба стрелка; в) ни один из стрелков не попадет в цель.

3. 9. Вероятность того, что откажет один мотор самолета равна 0, 01. На самолете 3 мотора. Предполагая, что отказ одного мотора не зависит от работы двух других моторов, найти вероятность того, что откажут все 3 мотора.

3. 10. Устройство содержит 2 независимо работающих элемента. Вероятности исправной работы элементов 0, 95 и 0, 98 соответственно. Найти вероятность отказа устройства, если для этого необходимо, чтобы отказали оба элемента.

3. 11. Радист трижды вызывает корреспондента. Вероятность того, что будет принят первый вызов равна 0, 2, второй – 0, 3, третий – 0, 4. Найти вероятность того, что корреспондент услышит вызов радиста, если все вызовы идут независимо друг от друга.

3. 12. Бросаются две симметричные игральные кости. Чему равна вероятность того, что сумма выпавших очков равна 8 (событие A), если известно, что эта сумма есть четное число (событие B)?

3. 13. Определить вероятность того, что наудачу взятое изделие будет 1-го сорта, если известно, что 4% всей продукции – брак, а 75% из небракованных изделий соответствует требованиям 1-го сорта.

3. 14. В коробке 6 одинаковых пронумерованных кубиков. Наудачу по одному извлекают все кубики. Найти вероятность того, что номера извлеченных кубиков появятся в возрастающем порядке.

3. 15. Известно, что вероятность выпуска сверла повышенной хрупкости (брак) равна 0, 02. Сверла укладываются в коробки по 10 штук. Чему равна вероятность того, что а) в коробке не окажется бракованных сверл; б) число бракованных изделий окажется не более трех?

3. 16. События A и B независимы. Являются ли независимыми события: а)  и ; б)  и .

3. 17. По цели производится n независимых выстрелов. Вероятность попадания при i-ом выстреле равна ( ). Найти вероятность того, что при n выстрелах будет не менее двух попаданий.

3. 18. Четыре поздравительных открытки разложены по четырем конвертам с адресами. Найти вероятность того, что а) хотя бы одна открытка попала в свой конверт; б) ни одна открытка не попала в свой конверт.

3. 19. В круг радиуса R вписан квадрат. Чему равна вероятность того, что поставленные наудачу внутри круга 2 точки окажутся внутри квадрата?

3. 20. Две одинаковые монеты радиуса r расположены внутри круга радиуса R, в который наудачу бросается точка. Определить вероятность того, что эта точка упадет на одну из монет, если монеты " не пересекаются".

3. 21. Доказать, что , .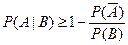

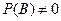3. 22. Пусть события A и B независимы, и независимы также события A и C, при этом . Доказать, что события  и  независимы.

3. 23. Сколько раз минимум нужно бросить игральную кость, чтобы с вероятностью, не меньшей 0, 9, хотя бы один раз выпала шестерка.

3. 24. Баллотируются два кандидата, причем за первого в урну опущено n, а за второго m бюллетеней (n> m). Какова вероятность того, что в ходе подсчета бюллетеней число подсчитанных голосов, поданных за первого, все время будет больше числа голосов, поданных за второго?

3. 25. Могут ли независимые события быть несовместными (возможные ответы: да, нет). Показать справедливость одного из ответов.