 |
5. Дискретные случайные величины и их числовые характеристики
|
|
|
|
5. ДИСКРЕТНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ И ИХ ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ
Основные понятия раздела
Случайная величина – это переменная, которая в результате опыта  может принять то или иное числовое значение в зависимости от случайных обстоятельств, которые выпадают из круга рассматриваемых условий
может принять то или иное числовое значение в зависимости от случайных обстоятельств, которые выпадают из круга рассматриваемых условий 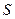 , но сопутствующих каждому испытанию.
, но сопутствующих каждому испытанию.
Случайная величина называется дискретной, если она может принимать только конечное или счетное множество значений.
Всякое соотношение, устанавливающее зависимость между возможными значениями СВ и их вероятностями, называется законом распределения вероятностей (ЗРВ). ЗРВ дискретной случайной величины можно представить в виде графика, таблицы или задать аналитически (ряд распределения, функция распределения).
Пусть X – случайная величина, а x – произвольное действительное число. Вероятность того, что X примет значение, меньшее чем x, называется функцией распределения вероятностей СВ X
 .
.
Основные свойства функции распределения вероятностей.
F1. Свойство монотонности: Функция распределения есть неубывающая функция, т. е.  , если
, если  .
.
F2. Свойство ограниченности: 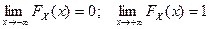 .
.
F3. Свойство непрерывности слева:  .
.
Математическим ожиданием дискретной случайной величины X называется число
 , (*)
, (*)
если существует (абсолютно сходится) сумма (*).
Основные свойства математического ожидания.
М1. Математическое ожидание константы равняется самой константе: 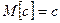 , где c– константа.
, где c– константа.
М2. Математическое ожидание от суммы случайных величин равняется сумме математических ожиданий этих величин:  .
.
М3. Математическое ожидание ограниченной случайной величины ограничено: если 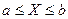 , то
, то  . Всегда
. Всегда 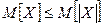 .
.
|
|
|
М4. Если  и
и 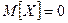 , то
, то 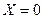 с вероятностью единица.
с вероятностью единица.
М5. Для произвольной функции  случайная величина
случайная величина  имеет математическое ожидание
имеет математическое ожидание 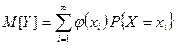 , если ряд существует (сходится абсолютно).
, если ряд существует (сходится абсолютно).
М6. Если  и
и 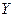 – взаимно независимые случайные величины с конечными математическими ожиданиями, то их произведение является случайной величиной с конечным математическим ожиданием:
– взаимно независимые случайные величины с конечными математическими ожиданиями, то их произведение является случайной величиной с конечным математическим ожиданием:  .
.
Моментом k-го порядка случайной величины X относительно константы С называется математическое ожидание 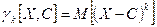 .
.
При  момент
момент  называют центральным и обозначают:
называют центральным и обозначают:
 .
.
При  момент
момент  называют начальным и обозначают:
называют начальным и обозначают:
 .
.
Факториальным моментом k-го порядка случайной величины X называется математическое ожидание 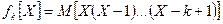 .
.
Дисперсией случайной величины X называется математическое ожидание квадрата уклонения X от ее математического ожидания
 .
.
Нетрудно убедиться, что  .
.
Величина  называется стандартным уклонением:
называется стандартным уклонением:  .
.
Основные свойства дисперсии.
D1. Дисперсия – величина неотрицательная:  . Дисперсия постоянной равняется нулю:
. Дисперсия постоянной равняется нулю: 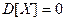 тогда и только тогда, когда
тогда и только тогда, когда  , где С – константа.
, где С – константа.
D2. Постоянный множитель выносится за знак дисперсии в квадрате:  . Постоянное слагаемое не влияет на величину дисперсии этой величины:
. Постоянное слагаемое не влияет на величину дисперсии этой величины: 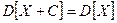 .
.
D3. Дисперсия суммы независимых случайных величин X и Y равна сумме их дисперсий: 
Задачи с решениями
1. Случайная величина X задана рядом распределения:
| X | -2 | -1 | |||
| P | 0, 1 | 0, 2 | 0, 2 | 0, 4 | 0, 1 |
Требуется: а) построить многоугольник распределения; б) построить функцию распределения и начертить ее график; в) найти вероятность того, что величина X примет значение, непревосходящее по абсолютной величине 1.
Решение.
 |
а) Многоугольник распределения представляет собой графическое изображение ряда распределения (Рис. 5. 1).
б) По определению  . Для построения функции распределения в качестве x будем брать значения X из заданного ряда распределения. Тогда в соответствии с определением имеем:
. Для построения функции распределения в качестве x будем брать значения X из заданного ряда распределения. Тогда в соответствии с определением имеем:
|
|
|
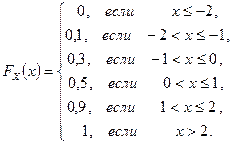
Построим график функции распределения вероятностей случайной величины X (Рис. 5. 2).
в) Используя свойства функции распределения, находим искомую вероятность
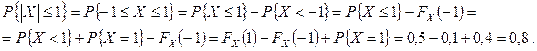
2. В урне 5 белых и 25 черных шаров. Вынимается 2 шара. Случайная величина X – число вынутых белых шаров. Построить ряд распределения и функцию распределения вероятностей величины X.
Решение. Вынимается 2 шара. Здесь возможны следующие ситуации: оба шара черные, один черный и один белый, оба шара белые. Следовательно, случайная величина X может принимать три значения: 0, 1, 2. Найдем вероятности, с которыми эти значения принимаются.
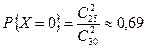 ;
;  ;
;  .
.

Условие нормировки выполняется: 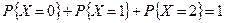 .
.
Запишем ряд распределения вероятностей:
| X | |||
| P | 0, 69 | 0, 29 | 0, 02 |
Построим функцию распределения заданной случайной величины на основе ее определения:

3. Построить ряд распределения и функцию распределения случайной величины X – числа попаданий мячом в корзину при двух независимых бросках, если вероятность попадания при одном броске равна 0, 4. Найти математическое ожидание и дисперсию этой случайной величины.
Решение. Заданная случайная величина принимает три значения: 0, 1, 2 со следующими вероятностями:
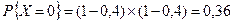 ;
;
 ;
;
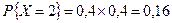 .
.
Условие нормировки выполняется: 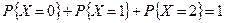 .
.
Ряд распределения выглядит следующим образом:
| X | |||
| P | 0, 36 | 0, 48 | 0, 16 |
Функция распределения имеет вид:

Заданная случайная величина является дискретной. Математическое ожидание дискретной величины определяется как сумма произведений значений случайной величины на вероятности, с которыми эти значения принимаются. Тогда  .
.
Используя свойства математического ожидания и определение дисперсии, находим 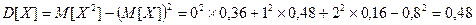 .
.
4. Из партии в 25 изделий, среди которых имеются 6 бракованных, выбраны случайным образом 3 изделия для проверки их качества. Построить ряд распределения случайного числа X бракованных изделий, содержащихся в выборке. Найти начальные, центральные и факториальные моменты четырех первых порядков.
Решение. Случайная величина X может принимать следующие значения: 0, 1, 2, 3. Определим соответствующие вероятности:
|
|
|
 ;
;  ;
;
 ;
; 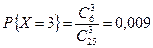 .
.
Условие нормировки выполняется: 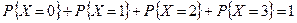 .
.
Ряд распределения выглядит следующим образом:
| X | ||||
| P | 0, 421 | 0, 446 | 0, 124 | 0, 009 |
По определению начальный момент k-ого порядка есть математическое ожидание случайной величины в степени k, т. е. 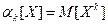 . Используя эту формулу, находим:
. Используя эту формулу, находим:
 ;
;
 ;
;
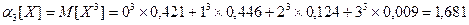 ;
;
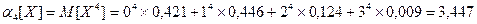 .
.
По определению центральный момент k-ого порядка есть величина, определяемая по формуле: 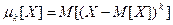 . На основе этой формулы и результатов вычисления
. На основе этой формулы и результатов вычисления 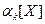 находим:
находим:
 ;
;

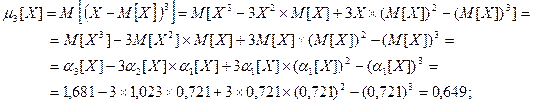

Факториальный момент k-ого порядка определяется следующим образом:  . Отсюда находим:
. Отсюда находим:
 ;
;



5. Математическое ожидание и дисперсия случайной величины X равны соответственно 2 и 10. Найти математическое ожидание и дисперсию величины  .
.
Решение. Зная свойства математического ожидания и дисперсии для линейного преобразования случайной величины, находим:
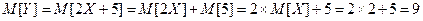 ;
;
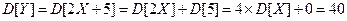 .
.
6. Найти широту и среднеквадратическое отклонение случайной величины, заданной рядом распределения:
| X | ||||
| P | 0, 4 | 0, 3 | 0, 2 | 0, 1 |
Решение. По определению широта есть разность между максимальным и минимальным значениями случайной величины. Обозначив широту через 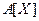 , находим
, находим  .
.
Среднеквадратическое отклонение есть корень квадратный из дисперсии. Найдем дисперсию по формуле  .
.
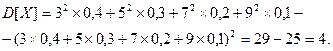
Отсюда получаем  .
.
7. Найти математическое ожидание и дисперсию: а) числа очков, выпадающих при бросании одной симметричной игральной кости; б) суммы очков, выпадающих при бросании n игральных костей.
Решение.
а) Прежде, чем найти математическое ожидание и дисперсию, запишем закон распределения вероятностей данной случайной величины:
| X | ||||||
| P | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
 ;
;
 ;
;
б) Обозначим через Y случайную величину, представляющую собой сумму из n величин X. Зная, что математическое ожидание суммы случайных величин равняется сумме математических ожиданий этих величин, получаем 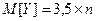 .
.
Величины, образующие Y, независимы (по условию эксперимента). В этом случае дисперсия также равняется сумме дисперсий, т. е. 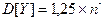 .
.
8. Найти математическое ожидание и дисперсию числа лотерейных билетов, на которые выпадут выигрыши, если приобретено 40 билетов, причем вероятность выигрыша равна 0, 05.
|
|
|
Решение. Случайная величина X – число лотерейных билетов, на которые выпадут выигрыши, подчиняется биномиальному закону распределения с параметрами:  и
и  . Зная свойства этого распределения, находим
. Зная свойства этого распределения, находим 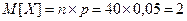 ;
;
 .
.
9. Распределение дискретной случайной величины X определяется формулой:
 .
.
Найти постоянную C и вероятность 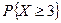 .
.
Решение. Постоянную C находим из условия нормировки:
 .
.
Вынесем C за знак суммы и преобразуем равенство к следующему виду:
 .
.
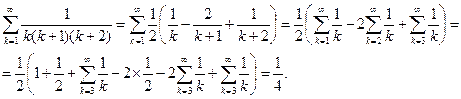
Следовательно,  .
.
Найдем теперь вероятность события, состоящего в том, что X примет значение, большее или равное 3:
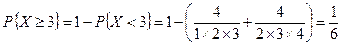 .
.
10. Случайные величины X и Y независимы, причем 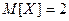 ,
,  ,
,  ,
, 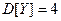 . Найти математическое ожидание и дисперсию величины
. Найти математическое ожидание и дисперсию величины  .
.
Решение. Зная свойства математического ожидания и дисперсии, находим: 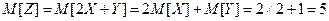 ;
;
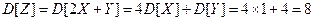 .
.
|
|
|


