Задачи для самостоятельной работы

5. 1. Случайная величина X может принимать любое целое положительное значение n с вероятностью, пропорциональной . Найти математическое ожидание величины X.

5. 2. В партии хлопка 20% коротких волокон. Случайно отбирается n волокон. Найти математическое ожидание и дисперсию числа коротких волокон среди случайно отобранных.

5. 3. Найти математическое ожидание и дисперсию индикатора события A, вероятность наступления которого равна p.

5. 4. Число -частиц, достигающих счетчика в некотором опыте, является случайной величиной X, распределенной по следующему закону:

X
P	0, 021	0, 081	0, 156	0, 201	0, 195	0, 151	0, 097	0, 064	0, 026	0, 001	0, 007

Найти: а) математическое ожидание и дисперсию числа частиц, достигающих счетчика; б) вероятность того, что число частиц, достигших счетчика, не меньше четырех.

5. 5. Бросаются две игральные кости. Пусть X – сумма очков, выпадающих на их верхних гранях. Написать закон распределения случайной величины X.

5. 6. Бросается n игральных костей. Найти математическое ожидание, дисперсию и центральный момент третьего порядка суммы очков на всех костях.

5. 7. Дан ряд распределения случайной величины X

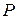
	0, 2	0, 3	0, 4	0, 1

Найти начальные и центральные моменты первых четырех порядков.

5. 8. Производятся независимые испытания трех приборов. Вероятность отказа каждого прибора соответственно равна 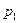,  и . Показать, что математическое ожидание числа отказавших приборов равно .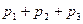

5. 9. Производится 30 независимых испытаний, в каждом из которых вероятность появления успеха равна 0, 2. Найти математическое ожидание и среднеквадратическое отклонение числа появления успехов в этих испытаниях.

5. 10. Производится три независимых опыта, в каждом из которых с равной вероятностью может быть получено целое число от 0 до 9. Построить ряд распределения суммы полученных чисел.

5. 11. Производятся независимые испытания, в каждом из которых с вероятностью 0, 8 может произойти событие A. Испытания производятся до первого появления события A. Общее число испытаний не больше 4. Найти математическое ожидание произведенных испытаний.

5. 12. Распределение случайной величины X определяется формулой:

.

Найти математическое ожидание X.

5. 13. В партии из 10 деталей имеются 8 стандартных. Наудачу отобраны 2 детали. Составить закон распределения вероятностей числа стандартных деталей среди отобранных.

5. 14. Распределение дискретной случайной величины задано рядом распределения:

X	-2	-1
P	0, 2	0, 2	0, 2	0, 2	0, 2

Найти математическое ожидание Y, если  и математическое ожидание Z, если .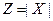

5. 15. В партии 10% нестандартных деталей. Наудачу отобраны 4 детали. Написать закон распределения вероятностей случайной величины X – числа нестандартных деталей среди четырех отобранных и построить функцию распределения вероятностей.

5. 16. Бросают n игральных костей. Найти математическое ожидание числа таких бросаний, в каждом из которых выпадет ровно m шестерок, если общее число бросаний равно N.

5. 17. В партии из 10 деталей содержится 3 нестандартных. Наудачу отобраны 2 детали. Найти математическое ожидание дискретной случайной величины X – числа нестандартных деталей среди двух отобранных.

5. 18. Брошены две игральные кости. Найти математическое ожидание суммы очков, если известно, что выпали разные грани.

5. 19. Бросаются три монеты. Требуется задать случайную величину X, равную числу выпавших " решеток", построить ряд распределения и функцию распределения величины X, если вероятность выпадения " герба" равна 0, 5.

5. 20. Доказать, что если X и Y независимы, то .

5. 21. Из партии, содержащей 100 изделий, среди которых имеется 10 дефектных, выбраны случайным образом 5 изделий для проверки их качества. Построить ряд распределения случайного числа X дефектных изделий, содержащихся в выборке.

5. 22. Изделия испытываются при перегрузочных режимах. Вероятности для каждого изделия пройти испытание равны 0, 8. Испытания независимы и заканчиваются после обнаружения первого изделия, не выдержавшего испытаний. Вывести формулу для ряда распределения числа испытаний.

5. 23. На пути движения автомашины четыре светофора. Каждый из них с вероятностью 0, 5 либо разрешает, либо запрещает автомашине дальнейшее движение. Построить многоугольник распределения вероятностей числа светофоров, пройденных автомашиной без остановки.

5. 24. Рабочий обслуживает n однотипных станков, расположенных на одной прямой. Расстояние между каждыми двумя соседними станками одинаково и равно а. Закончив обслуживание какого-либо станка, рабочий переходит к тому станку, который раньше других потребовал его внимания. Вероятности перехода от станка к станку равны между собой. Найти математическое ожидание длины перехода совершаемого рабочим.

5. 25. Какому условию должны удовлетворять независимые случайные величины X и Y, чтобы D[X·Y]=D[X]·D[Y].

5. 26. (Задача об оценке) Урна содержит шары, снабженные номерами от 1 до N. Пусть X – наибольший номер, полученный в результате n извлечений, если производится случайный выбор с возвращением. Событие  означает, что каждый из извлеченных номеров не превосходит k, так что 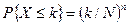. Найти математическое ожидание величины X.

⇐ Предыдущая6789101112131415Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: