 |
6. Непрерывные случайные величины и их числовые характеристики
|
|
|
|
6. НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ И ИХ ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ
Основные понятия раздела
Функции, представимые в виде: 
, называются абсолютно непрерывными функциями распределения. Функция 
называется плотностью распределения вероятностей.
Свойства плотности распределения вероятностей:
Р1. 
.
Р2. 
.
Математическим ожиданием непрерывной случайной величины 
называется число 
, если этот интеграл существует.
Медианой случайной величины с распределением 
называется такое значение аргумента m, для которого выполняются неравенства
.
Если функция распределения непрерывна, то существует, по меньшей мере, одно значение аргумента, для которого выполняется равенство
.
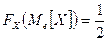Квантилью порядка 
случайной величины с распределением называется корень уравнения 
.
Модой распределения непрерывной случайной величины с плотностью называют то значение аргумента, при котором плотность достигает максимума: 
.
Задачи с решениями
1. Случайная величина X задана функцией распределения:
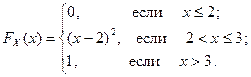
а) Найти плотность распределения вероятностей случайной величины X.
б) Определить вероятность попадания величины X в интервал (1; 2, 5).
Решение.
а) По определению плотность есть производная от функции распределения. Взяв производную от 
на каждом участке ее существования, имеем: 
б) Вероятность попадания непрерывной случайной величины в заданный интервал определяется на основе свойства функции распределения вероятностей: 
.
2. Случайная величина X имеет плотность распределения вероятностей
а) Найти функцию распределения вероятностей случайной величины X.
б) Вычислить вероятность того, что в результате двух испытаний величина X только один раз примет значение из интервала 
.
|
|
|
Решение.
а) Функция распределения вероятностей есть интеграл от плотности распределения вида: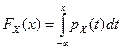 
. Применим это определение для нашего случая, используя свойства определенного интеграла:
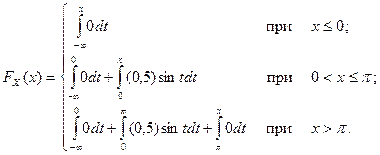
Окончательно получаем
б) Обозначим через 
– событие, состоящее в том, что в результате испытания величина X примет значение из интервала . Вероятность этого события находится на основе свойств функции распределения вероятностей для непрерывной случайной величины:
.
Отсюда вероятность искомого события (обозначим его через B) будет
.
3. Плотность распределения вероятностей случайной величины X равна
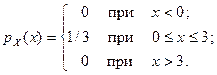
а) Построить функцию распределения вероятностей случайной величины X и начертить ее график.
б) Найти математическое ожидание, дисперсию и среднеквадратическое отклонение величины X.
Решение.
а) Выразив функцию распределения вероятностей через плотность распределения вероятностей, находим
Окончательно имеем
График этой функции представлен на рисунке 6. 1.
б) Для определения математического ожидания, дисперсии и среднеквадратического отклонения воспользуемся их определениями.
.
.
.
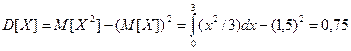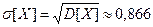4. Случайная величина X 
задана плотностью распределения вероятностей:
Найти: а) математическое ожидание и дисперсию случайной величины X; б) вероятность попадания величины X в интервал 
.
Решение.
а) Согласно определений
;
.
 |
б) Вычислим 
и найдем
.
5. Случайная величина X имеет плотность распределения вероятностей
а) Построить функцию распределения ;
б) Найти вероятность того, что случайная величина X примет значение, меньшее, чем ее математическое ожидание.
Решение.
а) Пользуясь определением, найдем функцию распределения случайной величины X:
б) Для нахождения вероятности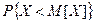 
воспользуемся определением функции распределения вероятностей, но прежде вычислим значение математического ожидания:
|
|
|
;
.
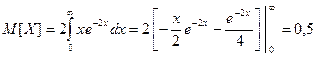6. Точка брошена наудачу внутрь круга радиуса R. Вероятность попадания точки в любую область, расположенную внутри круга, пропорциональна площади этой области. Найти функцию распределения и дисперсию расстояния от точки до центра круга.
Решение. Случайная величина X – это расстояние от брошенной точки до центра круга, т. е. 
. По определению площади круга неравенство можно преобразовать к виду: 
. Далее, используя определение функции распределения, имеем 
. Отсюда окончательно получаем
Для нахождения дисперсии необходимо найти плотность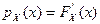 
.
7. Случайная величина 
имеет нормальное распределение
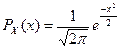
Что больше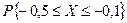 
или 
?
Решение. Найдем соответствующие вероятности по таблице стандартного нормального распределения
.
.
Следовательно >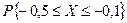 
.
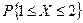8. Случайная величина эксцентриситета детали имеет распределение Рэлея:
Найти плотность распределения вероятностей, медиану и моду эксцентриситета.
Решение. Плотность распределения найдем, воспользовавшись ее определением 
.
Медиана (или квантиль порядка 0, 5) есть такое значение x непрерывной случайной величины, при котором выполняется равенство: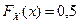 
.
Преобразуя уравнение
;
;
,
находим решение: 
есть значение медианы случайной величины эксцентриситета детали.
Если случайная величина X абсолютно непрерывна, то значения x, в которых плотность достигает своего максимального значения, называются модами. Для нахождения моды заданного распределения запишем уравнение 
. Уравнение 
имеет два решения: 
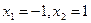. По условию случайная величина принимает только неотрицательные значения. Следовательно, 
.
9. Дана плотность распределения вероятностей случайной величины X:
Найти: а) начальные и центральные моменты первых четырех порядков; б) коэффициенты асимметрии и эксцесса этой случайной величины.
Решение.
а) Для нахождения начальных и центральных моментов воспользуемся их определениями (см. задачу 4, раздел 5).
;
;
;
;
;
;
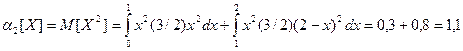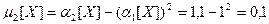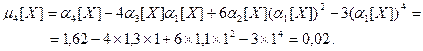
б) Коэффициенты асимметрии и эксцесса вычисляются по следующим формулам:
;
.
10. Плотность распределения вероятностей случайной величины X имеет вид:
а) Вычислить коэффициент A.
|
|
|
б) Найти функцию распределения вероятностей величины X.
в) Определить вероятность попадания величины X в интервал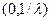 
.
Решение.
а) Коэффициент A находим из условия нормировки: 
. Перепишем это уравнение применительно к нашему случаю: 
. Проинтегрировав по частям дважды и подставив пределы, получаем уравнение: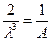 
. Отсюда имеем: 
.
б) Так как задана плотность распределения, функцию распределения вероятностей случайной величины X найдем как интеграл от плотности:
.
в) Вероятность попадания в интервал определяется как интеграл от плотности в заданных пределах, т. е.
.
|
|
|
