 |
Задачи для самостоятельной работы
|
|
|
|
6. 1. Случайная величина X задана плотностью распределения вероятностей:
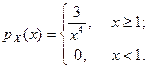
Найти функцию распределения вероятностей, математическое ожидание и дисперсию величины X.
6. 2. Случайная величина X задана на всей оси функцией распределения вероятностей: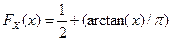 
.
а) Определить вероятность того, что в результате испытания величина X примет значение из интервала (0, 1).
б) Найти плотность распределения вероятностей величины X.
в) Вычислить моду величины Х.
6. 3. Случайная величина X задана функцией распределения вероятностей:
а) Найти плотность распределения вероятностей случайной величины X.
б) Определить вероятность того, что в результате трех независимых испытаний величина X попадет в интервал (0, 1) не менее двух раз.
в) Вычислить математическое ожидание и дисперсию величины X.
6. 4. Случайная величина X задана функцией распределения вероятностей:
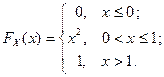
а) Найти плотность распределения вероятностей случайной величины 
и построить ее график.
б) Определить вероятность того, что в результате четырех независимых испытаний величина X ровно три раза примет значение из интервала (0, 25, 0, 75).
в) Вычислить медиану величины X.
6. 5. При каком значении a функция 
является плотностью распределения вероятностей случайной величины X?
6. 6. Плотность распределения вероятностей случайной величины X имеет вид
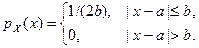
Найти математическое ожидание и дисперсию величины X.
6. 7. Вероятность обнаружения затонувшего судна за время поиска X задается формулой:
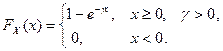
Определить среднее время поиска, необходимое для обнаружения судна.
6. 8. Функция распределения вероятностей случайной величины X имеет вид:
Найти плотность распределения вероятностей, математическое ожидание и дисперсию величины X.
|
|
|
6. 9. Случайная величина X распределена по закону
Найти математическое ожидание, моду и медиану величины X.
6. 10. Функция распределения
в ряде случаев характеризует срок службы элементов электронной аппаратуры. Найти плотность распределения 
и вычислить моду величины X.
6. 11. Случайная величина X задана функцией распределения вероятностей 
. Найти плотность распределения вероятностей величины X и вероятность попадания X в интервал 
.
6. 12. Плотность распределения случайной величины Z имеет вид
Найти математическое ожидание и дисперсию величины X, если 
.
6. 13. Функция распределения вероятностей непрерывной случайной величины X (времени безотказной работы некоторого устройства) имеет вид:
Найти вероятность безотказной работы устройства за время T.
6. 14. Случайная величина X задана плотностью распределения вероятностей:
Найти математическое ожидание и дисперсию величины X.
6. 15. Случайная величина X задана плотностью распределения вероятностей:
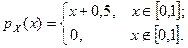
Найти математическое ожидание величины 
.
6. 16. Случайная величина X задана плотностью распределения вероятностей:
Найти моду и медиану, коэффициенты асимметрии и эксцесса величины X.
6. 17. Случайная величина X распределена равномерно с 
и 
. Найти плотность распределения вероятностей величины X.
6. 18. Найти медиану и моду распределения вероятностей, плотность которого задается формулой 
.
6. 19. Случайная величина X имеет показательное распределение, заданное плотностью
Найти коэффициенты асимметрии и эксцесса величины X.
6. 20. Найти квантиль порядка 0, 5 для случайной величины, имеющей в интервале 
плотность распределения вероятностей
.
6. 21. Случайная величина X подчиняется бета-распределению с плотностью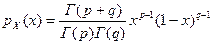 
, 
. Найти начальные моменты трех первых порядков величины X.
6. 22. Случайная величина X задана плотностью распределения вероятностей 
, где n – целое положительное число, большее 1. Определить постоянную A, математическое ожидание и дисперсию величины X.
|
|
|
6. 23. Случайная величина X имеет распределение Парето, заданное функцией распределения вероятностей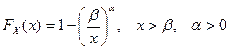 
. Найти медиану и квантиль порядка 0, 5 величины X.
6. 24. Плотность распределения вероятностей случайных амплитуд X боковой качки корабля определяется формулой
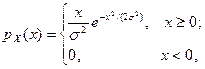
где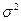 
– дисперсия угла крена. Одинаково ли часто встречаются амплитуды, меньшие и большие средней?
6. 25. Случайная величина X имеет треугольное распределение (распределение Симпсона):
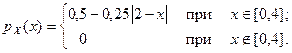
Вычислить моду, медиану, математическое ожидание, дисперсию, коэффициенты асимметрии и эксцесса величины X.
6. 26. Пусть в качестве функции распределения вероятностей некоторой случайной величины используется кривая Кантора. Выяснить, является ли эта функция непрерывной и дифференцируемой.
|
|
|
